1 Метод прямого включения

Сначала рассмотрим метод сортировки, который является базовым для метода Шелла. Метод прямого включения заключается в следующем. Начиная с i = 2, i=2,… n, берём очередной i–й элемент массива и включаем его на нужное место среди первых (i-1) элементов, при этом все элементы, которые больше a_i сдвигаются на одну позицию вправо.

Пример. Отсортировать слово методом прямого включения.

Условные обозначения

i-тый элемент

сравнение элемента X с i-тым элементом

сдвиг элемента на одну позицию вправо

Рисунок 5 - Метод прямого включения

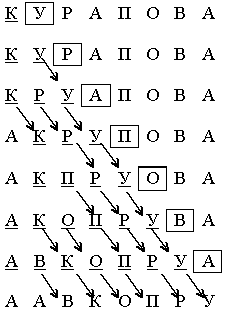
Алгоритм на псевдокоде

Метод прямого включения

DO (i: = 2, 3, … n)

   t: = a_i, j: =i-1

   DO (j > 0 и t < a_j)

      a_j+1:= a_j

      j: = j-1

   OD

   a_j+1:= t

OD

Для метода прямого включения справедливы следующие оценки величин М и С.

C_min £ С_сред £ C_max, где C_min = n-1, C_max = ,

М_min £ М_сред £ М_max, где М_min = 2(n-1), M_max = .

Минимальные и максимальные значения величин С и М достигаются на прямо отсортированном и обратно отсортированном массивах соответственно. Таким образом, средняя трудоемкость этого метода имеет квадратичный порядок, т.е. С = О(n²) М = О(n²), при n® ¥ .

Метод прямого включения устойчивый.

2 Метод Шелла

На базе метода прямого включения разработан алгоритм, обеспечивающий значительную производительность сортировки. Мы заметили, что в методе прямого включения, чем больше упорядочен массив, тем меньше операций требуется для его сортировки. При сортировке уже упорядоченного массива трудоемкость имеет линейный порядок. Поэтому имеет смысл попытаться предварительно несколько улучшить порядок элементов в массиве, а затем отсортировать массив методом прямого включения.

Предварительное упорядочивание будем проводить с помощью k – сортировок. Суть k – сортировки заключается в следующем. Массив разбивается на последовательности с шагом k

a_i, a_k+i, a_2k+i, …,a_[n/k]k+i, i = 1, 2,…,k

и сортировка происходит только внутри этих последовательностей.

Обозначим через H последовательность из m возрастающих шагов

H=(h₁, h₂, … h_m), где h₁=1, h₁ < h₂ < h₃ < … < h_m

Метод Шелла состоит в последовательном проведении h_i-сортировки, i=m, m-1,…, 1, причем h₁=1 гарантирует, что массив будет полностью отсортирован, поскольку 1-сортировка является методом прямого включения.

Пример. Отсортировать слово методом Шелла. Последовательность шагов выберем следующим образом h₁=1, h₂=2.

Рисунок 6 - Метод Шелла

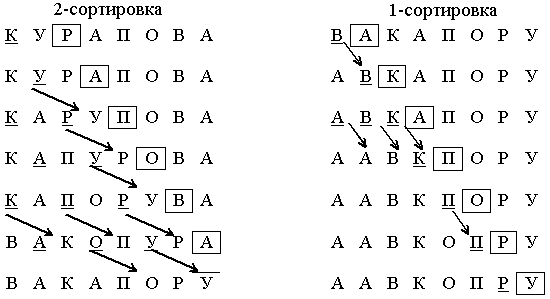
Алгоритм на псевдокоде

Сортировка методом Шелла

DO (k=h_m, h_m-1, … 1)

   DO (i=k+1, k+2, … n)

      t: = a_i, j: =i-k

      DO (j>0 и t < a_j)

         a_j+k: = a_j

         j: = j-k

      OD

   a_j+k: = t

   OD

OD

Эффективность метода зависит от выбора значений шагов. Последовательность значений шагов, которая дает наилучшую трудоемкость, пока неизвестна, метод продолжает исследоваться, но существует и часто используется следующая последовательность шагов, предложенная Кнутом.

h₁=1, h_i=2h_i-1+1, i=2,… m, m=

При такой последовательности шагов средний порядок трудоёмкости O(n^1.2), n → ∞. Таким образом, метод Шелла существенно быстрее методов с квадратичной трудоемкостью. Метод Шелла не устойчив.

Контрольные вопросы

1. Сформулируйте основную идею метода прямого включения.
2. Каковы теоретические оценки сложности метода прямого включения?
3. Что такое n-сортировка?
4. Как метод Шелла зависит от начальной отсортированности массива?
5. Какова трудоемкость метода Шелла?
6. Является ли метод Шелла устойчивым?
7. Каким образом выбирается последовательность шагов в методе Шелла?