1 Метод прямого выбора

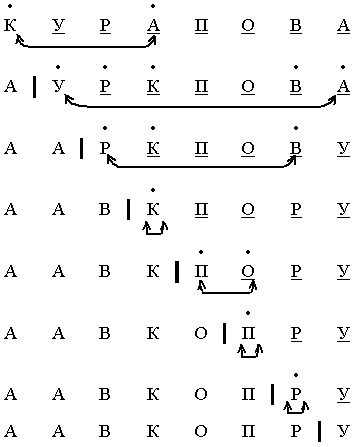
Один из самых простых методов сортировки, метод прямого выбора, заключается в следующем. Находим наименьший элемент массива и обмениваем его с первым элементом массива. Таким образом, первый элемент можно больше не рассматривать. Среди оставшихся элементов находим наименьший элемент и обмениваем его со вторым элементом массива. Среди оставшихся элементов находим наименьший и переставляем его на третье место и т. д.

Пример. Упорядочим слово методом прямого выбора.

Условные обозначения

сравнение элемента Х с текущим максимальным элементом

текущий максимальный элемент

Перестановка элементов

Рисунок 2 - Метод прямого выбора

Алгоритм на псевдокоде

Метод прямого выбора

DO (i = 1, 2, ... n-1)

    k := <номер наименьшего элемента из a_i,… a_n>

    a_i ↔ a_k

OD

Дадим оценку трудоёмкости метода прямого выбора. В данном случае можно найти точные выражения для М и С. Поскольку на каждой итерации происходит точно один обмен, то M = 3(n-1). Определим теперь количество сравнений. На первом этапе имеем (n-1) сравнений, на втором – (n-2) сравнений, на i-том этапе происходит (n- i) сравнений и т.д. Суммируя, получим C =

Отметим важные особенности метода прямого выбора. Метод не зависит от исходной отсортированности массива, т.е. значения М и С не меняются, даже если сортируется уже отсортированный массив. Сортировка методом прямого выбора неустойчива.

2 Пузырьковая сортировка

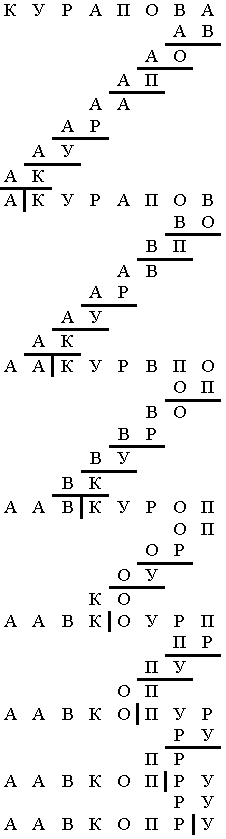
Популярный метод пузырьковой сортировки заключается в следующем. Двигаясь от конца массива к его началу, будем сравнивать между собой соседние элементы. При этом если правый элемент a_j будет меньше чем левый a_j-1, j=n, n-1, … ,2, то поменяем их местами. Таким образом, при первом проходе наименьший элемент переместится на первое место и можно не учитывать его при сортировке оставшейся части массива. При втором проходе наименьший элемент из оставшихся “всплывёт” на второе место. Через (n-1) итераций массив будет отсортирован.

Пример. Отсортировать слово методом пузырьковой сортировки. Подчёркнуты те пары, в которых произошёл обмен. Вертикальной чертой ограничена отсортированная часть массива.

Рисунок 3 - Пузырьковая сортировка

Алгоритм на псевдокоде

Пузырьковая сортировка

Обозначим i – номер итерации, j – индекс правого элемента в текущей паре.

DO (i= 1, 2, ... n-1)

    DO (j= n, n-1, ... i+1)

        IF (a_j < a_j-1) a_j ↔ a_j-1 FI

    OD

OD

Проанализируем сложность пузырьковой сортировки. Количество сравнений в методе прямого выбора и в методе пузырьковой сортировки одинаково и не зависит от исходной отсортированности массива. Однако количество пересылок M зависит от того, как часто выполняется условие a_j < a_j-1. Можно определить максимальное и минимальное значения М_min £ M_сред £ M_max,. где

М_min = 0, при сортировке упорядоченного по возрастанию массива.

M_max = 3C = , при сортировке упорядоченного по убыванию массива.

Отсюда следует, что M_сред=О(n²), при n® ¥

Таким образом, пузырьковая сортировка сильно зависит от исходной упорядоченности массива по количеству сравнений. Метод обеспечивает устойчивую сортировку.

3 Шейкерная сортировка

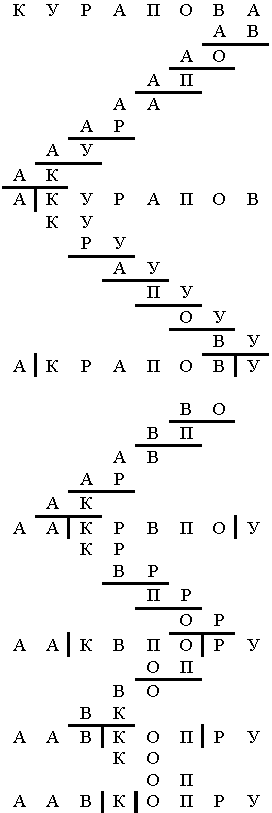
Анализируя метод пузырьковой сортировки можно отметить два обстоятельства. Во-первых, если при движении по части массива перестановки не происходят, то эта часть массива уже отсортирована и, следовательно, ее можно исключить из рассмотрения. Во-вторых, при движении от конца массива к началу минимальный элемент “всплывает” на первую позицию, а максимальный элемент сдвигается только на одну позицию вправо. Эти две идеи приводят к следующим модификациям в методе пузырьковой сортировки. Границы рабочей части массива (т.е. части массива, где происходит движение) устанавливаются в месте последнего обмена на каждой итерации. Массив просматривается поочередно справа налево и слева направо.

Пример. Отсортировать слово методом шейкерной сортировки. Подчёркнуты те пары, в которых произошёл обмен. Вертикальной чертой ограничена рабочая часть массива.

Рисунок 4 - Шейкерная сортировка

Алгоритм на псевдокоде

Метод шейкерной сортировки

Обозначим

    L – левая граница рабочей части массива.

    R – правая граница рабочей части массива.

    n – количество элементов в массиве

    L: = 1, R: = n, k: = n,

    DO

        DO (j =R, R-1, ... L+1)

            IF (a_j < a_j-1) a_j ↔ a_j-1, k: = j FI

        OD

        L: = k

        DO (j: = L, L+1, ... R-1)

            IF (a_j > a_j+1) a_j ↔ a_j+1, k: = j, FI

        OD

        R: = k

    OD (L < R)

Оценим трудоемкость метода. Количество пересылок такое же, как и в методе пузырьковой сортировки M_сред=О(n²), при n® ¥ . Улучшения в методе шейкерной сортировки приводят к снижению количества сравнений. Точное выражение для величины С получить не удается, поэтому определим границы, в которых изменяется С. Если сортируется массив, в котором элементы расположены в порядке возрастания, то в методе шейкерной сортировки достаточно один раз просмотреть массив. Тогда С_min = n-1, где n – количество элементов в массиве. Если массив отсортирован в обратном порядке, то на каждой итерации границы слева и справа сдвигаются на одну позицию и С_max = . Следовательно, С_сред=О(n²), при n® ¥ . Таким образом, как и пузырьковая сортировка, метод шейкерной сортировки сильно зависит от исходной упорядоченности массива по количеству сравнений. Метод обеспечивает устойчивую сортировку.

Контрольные вопросы

1. Сформулируйте основную идею метода прямого выбора.
2. Каковы теоретические оценки сложности метода пузырьковой сортировки?
3. Как метод пузырьковой сортировки зависит от начальной отсортированности массива?
4. Какова трудоемкость метода шейкерной сортировки?
5. Является ли метод шейкерной сортировки устойчивым?