1 Пирамидальная сортировка

Пирамидальная сортировка основана на алгоритме построения пирамиды. Последовательность a_i, a_i+1,…,a_k называется (i,k)-пирамидой, если неравенство

a_j≤min(a_2j, а_2j+1) (*)

выполняется для каждого j, j=i,…,k для которого хотя бы один из элементов a_2j, a_2j+1 существует.

Например, массив А является пирамидой, а массив В ¾ не является.

А=(а₂ , а₃ , а₄ , а₅ , а₆ а₇ , а₈ )=(3, 2, 6, 4, 5, 7)

В=(b₁, b₂, b₃, b₄, b₅, b₆, b₇)=(3, 2, 6, 4, 5, 7)

Свойства пирамиды

1. Если последовательность a_i, a_i+1,…,а_k-1, a_k является (i, k)-пирамидой, то последовательность a_i+1,…,a_k-1, полученная усечением элементов с обоих концов последовательности, является (i+1, k-1)пирамидой.
2. Если последовательность a₁…a_n – (1, n)-пирамида, то а₁ – минимальный элемент последовательности.
3. Если a₁, a₂…,a_n/2,a_n/2+1,…a_n-произвольная последовательность, то последовательность a_n/2+1,…,a_n является (n/2+1, n)-пирамидой.

Процесс построения пирамиды выглядит следующим образом. Дана последовательность a_s+1,…,a_k, которая является (s+1, k)-пирамидой. Добавим новый элемент х и поставим его на s-тую позицию в последовательности, т.е. пирамида всегда будет расширяться влево. Если выполняется (*), то полученная последовательность – (s, k)-пирамида. Иначе найдутся элементы a_2s+1,a_2s такие, что либо a_2s < a_s либо a_2s+1 < a_s.

Пусть имеет место первый случай, второй случай рассматривается аналогично. Поменяем местами элементы a_s и a_2s. В результате получим новую последовательность a_s^’,a_s+1,…, a_2s^’,…, a_k. Повторяем все действия для элемента a_2s^’ и т.д. пока не получим (s, k)-пирамиду.

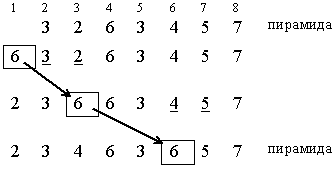
Пример. Добавим в (2, 8)-пирамиду новый элемент х=6.

Условные обозначения:

новый элемент

сравнение с включаемым элементом

обмен элементов

Рисунок 7- Добавление в пирамиду нового элемента

Алгоритм на псевдокоде

Построение (L,R)-пирамиды

a_L+1,…,a _R – на входе пирамида (L+1,R)

a_L –новый элемент

x:= a_L, i:=L

DO

   j:=2i

   IF (j>R) OD

   IF((j<R) и (a_j+1£ a_j)) j=j+1 FI

   IF (x£a_j) OD

   a_i= a_j

   i:=j

OD

a_i:=x

Величины М и С в процессе построения (L, R)-пирамиды имеют следующие оценки M_пир≤log (R/L)+2, C_пир≤2 log (R/L)

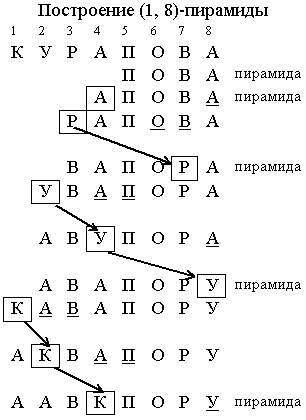
Пирамидальная сортировка производится в два этапа. Сначала строится пирамида из элементов массива. По свойству (3) правая часть массива является (n/2+1, n)-пирамидой. Будем добавлять по одному элементу слева, расширяя пирамиду, пока в неё не войдут все элементы массива. Тогда по свойству (2) первый элемент последовательности – минимальный.

Произведём двустороннее усечение: уберём элементы a₁,a_n. По свойству (1) оставшаяся последовательность является (2, n-1)-пирамидой. Элемент a₁ поставим на последнее место, а элемент a_n добавим к пирамиде a₂,…,a_n-1 слева. Получим новую (1, n-1)-пирамиду. В ней первый элемент является минимальным. Поставим первый элемент пирамиды на позицию n-1, а элемент a_n-1 добавим к пирамиде a₂,…,a_n-1, и т.д. В результате получим обратно отсортированный массив.

Пример. Отсортировать слово методом пирамидальной сортировки.

Рисунок 8 - Пирамидальная сортировка

Алгоритм на псевдокоде

Пирамидальная сортировка

L:=ën/2û

DO (L>0)

   Построение (L,n) пирамиды>

   L:=L-1

OD

R:=n

DO (R>1)

   a₁↔a_R

   R:=R-1

   Построение (1,R) пирамиды >

OD

Общее количество операций сравнений и пересылок для пирамидальной сортировки: C ≤ 2n log n+n+2, M ≤ n log n+6.5n-4. Таким образом, С=O(n log n), М=O(n log n) при n → ∞.

Отметим некоторые свойства пирамидальной сортировки. Метод пирамидальной сортировки неустойчив и не зависит от исходной отсортированности массива.

2 Метод Хоара

Метод Хоара или метод быстрой сортировки заключается в следующем. Возьмём произвольный элемент массива х. Просматривая массив слева, найдём элемент a_i ≥x. Просматривая массив справа, найдём a_j ≤x. Поменяем местами a_i и a_J . Будем продолжать процесс просмотра и обмена, до тех пор пока i не станет больше j. Тогда массив можно разбить на две части: в левой части все элементы не больше х, в правой части массива не меньше х. Затем к каждой части массива применяется тот же алгоритм.

Пример: Отсортировать слово методом быстрой сортировки.

Условные обозначения:

ведущий элемент

сравнение с ведущим элементом при просмотре справа

сравнение с ведущим элементом при просмотре слева

| разделение массива на части

обмен элементов

индекс i

индекс j

Рисунок 9 - Метод Хоара

Алгоритм на псевдокоде

Сортировка части массива с границами (L,R).

Обозначим: L-левую границу рабочей части массива

R-правую границу рабочей части массива

х:=а_L, i:=L, j:=R,

DО (i£ j)

   DО (a_i<x) i:=i+1 OD

   DО (a_j>x) j:=j-1 OD

   IF (i<=j)

      a_i↔ a_j,, i:=i+1, j:=j-1

   FI

OD

   IF (L<j)

      <Сортировка части массива с границами (L,j)>

   FI

   IF (i<R)

      <Сортировка части массива с границами (i,R)>

   FI

Очевидно, трудоёмкость метода существенно зависит от выбора элемента х, который влияет на разделение массива. Максимальные значения М и С для метода быстрой сортировки достигаются при сортировке упорядоченных массивов (в прямом и обратном порядке). Тогда в этом случае в одной части остаётся только один элемент (минимальный или максимальный), а во второй – все остальные элементы. Выражения для М и С имеют следующий вид

M=3(n-1), C=(n²+5n+4)/2

Таким образом, в случае упорядоченных массивов трудоёмкость сортировки имеет квадратичный порядок.

Элемент a_m называется медианой для элементов a_L…a_R, если количество элементов меньших a_m равно количеству элементов больших a_m с точностью до одного элемента (если количество элементов нечётно). В примере буква К- медиана для КУРАПОВАЕ.

Минимальная трудоемкость метода Хоара достигается в случае, когда на каждом шаге алгоритма в качестве ведущего элемента выбирается медиана массива. Количество сравнений в этом случае C=(n+1)log(n+1)-(n+1). Количество пересылок зависит от положения элементов, но не может быть больше одного обмена на два сравнения. Поэтому количество пересылок – величина того же порядка, что и число сравнений. Асимптотические оценки для средних значений М и С имеют следующий вид

С=О(n log n), М=О(n log n) при n → ∞.

Метод Хоара неустойчив.

3 Проблема глубины рекурсии

В теле подпрограммы доступны все объекты, описанные в основной программе, в том числе и имя самой подпрограммы. Это позволяет внутри тела подпрограммы осуществлять её вызов. Процедуры и функции, организующие вызовы “самих себя” называются рекурсивными. Рекурсия широко используется в программирование, потому что многие математические алгоритмы имеют рекурсивную природу.

В качестве примера приведём известный алгоритм вычисления факториала неотрицательного целого числа:

0!=1

1!=1

n!=(n-1)!*n

function fact (n:word):longint;

   begin

      if (n=0) or (n=1) then fact:=1

      else fact:=fact(n-1)*n;

   end;

Рисунок 10 - Схема вызовов при вычислении 4!

Рекурсивное оформление программы более компактно, наглядно и эффективно. Но существует опасность переполнения стека. Каждый вызов подпрограммы требует специально отведённой области памяти, называемой фреймом. В ней хранятся фактические параметры, адреса возврата, локальные переменные и регистры УП.

Фрейм

Практический параметр

Адрес возврата

Регистры из программы

Локальные переменные

Рисунок 11 - Структура фрейма

При выходе из программы эта память освобождается. Но если подпрограмма вызывает другую подпрограмму или саму себя, то в дополнение к существующему фрейму создаётся новый, т.е. n вложенных вызовов требуют выделения n фреймов в памяти.

Рассмотренный алгоритм Хоара может потребовать n вложенных вызовов (n – размер массива), т.е. глубина рекурсии достигает n. Это большой недостаток предложенного алгоритма. Попробуем уменьшить глубину рекурсии до log n. В рассмотренном алгоритме производится 2 рекурсивных вызова. Но один из них можно заменить простой итерацией, т.е. для одной части массива будем применять рекурсию, а для другого – простую итерацию. Чтобы уменьшить глубину рекурсии нужно делать рекурсивный вызов для меньшей по размеру части массива. Тогда в худшем случае, когда размеры правой и левой частей будут одинаковые, максимальная глубина рекурсии будет не больше log n. Например, для массива из 1 млн. элементов понадобиться одновременно менее 20 фреймов в памяти. Запишем новую версию алгоритма:

Алгоритм на псевдокоде

Сортировка части массива (L,R)

DO (есть хотя бы 2 элемента, т.е. L<R)

    <разделение> (как в 1 версии)

   IF (левая часть длиннее правой, т.е.j-L>R-i)

      Сортировка части массива (i,R)

      R:=j

   Else

      Сортировка части массива (L,j)

      L:=i;

   FI

OD

Контрольные вопросы

1. Дайте определение пирамиды.
2. Назовите основные свойства пирамиды
3. Какова сложность пирамидальной сортировки?
4. Сформулируйте основную идею метода Хоара.
5. Какова сложность метода Хоара?
6. Как зависит метод Хоара от начальной отсортированности массива?