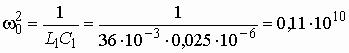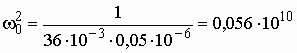Аналоговые устройства аппаратуры связи
ВведениеГлава 1. Передаточные функции и частотные характеристики
Примеры к Главе 1
Вопросы и задания для самопроверки
Глава 2. Электрические фильтры
Примеры к Главе 2
Вопросы и задания для самопроверки
Глава 3. Амплитудные корректоры
Примеры к Главе 3
Вопросы и задания для самопроверки
Глава 4. Фазовые корректоры
Примеры к Главе 4
Вопросы и задания для самопроверки
Глава 5. Нелинейные преобразователи
Примеры к Главе 5
Вопросы и задания для самопроверки
Глава 6. Генераторы
Примеры к Главе 6
Вопросы и задания для самопроверки
Литература
Введение
Бурное вторжение в технику передачи информации цифровых транспортных систем и цифровых средств коммутации создало иллюзию, что аналоговые устройства доставки сообщений остались далеко в прошлом. Поддержанию таких представлений способствует во многом создавшийся в научных и производственных публикациях перевес в сторону цифровых телекоммуникационных технологий.
На самом деле техническая революция, происходящая сейчас в сфере телекоммуникаций и информатики, не сметает напрочь аналоговую технику, а скорее, наоборот, предполагает органичное взаимодействие аналоговых и цифровых способов организации связи. Подобное имеет место, например, в современных системах подвижной радиосвязи, в сетях проводного и радиодоступа, оптических системах связи и др. Такие понятия, как фильтрация, генерация, модуляция, коррекция и т. п. еще многие десятилетия останутся в арсенале специалистов радиотехники, связи и информатики.
Более того, общая теория фильтров, генераторов, модуляторов, корректоров предполагает создание математических моделей этих устройств и описание на их основе происходящих физических процессов. Реализация же данных моделей может быть осуществлена как на основе аналоговой, так и на основе цифровой техники.
Материал предлагаемого читателю учебного пособия является частью дисциплины “Теория электрических цепей”, которая изучается студентами практически всех специальностей вузов и колледжей радиотехники и связи. Он посвящен теории и практике аналоговых устройств аппаратуры связи.
Учебные пособия предназначено для самостоятельного изучения описываемых разделов дисциплины. Это в значительной мере определило стиль построения книги. В качестве подзаголовков текста использованы ключевые фразы, сразу же вводящие читателя в суть предлагаемого материала. Текст книги насыщен большим количеством примеров. В конце основных разделов приведены контрольные вопросы и задания, упражнения с ответами, способствующие самоконтролю усвоения материала.
Предложенная структура книги, а также стремление авторов изложить материал ясно и доходчиво, делает это учебное пособие особенно полезным для системы дистанционного образования, где основной упор ставится на самостоятельное приобретение знаний.
Авторы будут признательны читателям за их критические замечания и пожелания, которые следует направлять по адресу: Россия, 630102, Новосибирск, ул. Кирова, 86, СибГУТИ, кафедра ТЭЦ.
Глава 1. Передаточные функции и частотные характеристики

Электрическую цепь любой сложности, имеющую две пары зажимов для подключения к источнику и приемнику электрической энергии, в технике связи называют четырехполюсником. Зажимы, к которым подключается источник, называются входными, а зажимы, к которым присоединяется приемник (нагрузка) – выходными зажимами (полюсами).
В общем виде четырехполюсник изображают,
как показано на рис. 1.1. К входу четырехполюсника 1–1ў подключен источник
электрической энергии с комплексным действующим значением напряжения ![]() и
внутренним сопротивлением
и
внутренним сопротивлением ![]() .
К выходным зажимам 2–2ў присоединена нагрузка с сопротивлением
.
К выходным зажимам 2–2ў присоединена нагрузка с сопротивлением ![]() .
К входным зажимам приложено напряжение с комплексным действующим значением
.
К входным зажимам приложено напряжение с комплексным действующим значением ![]() ,
к выходным – с комплексным действующим значением
,
к выходным – с комплексным действующим значением ![]() .
Через входные зажимы протекает ток с комплексным действующим значением
.
Через входные зажимы протекает ток с комплексным действующим значением ![]() ,
через выходные зажимы – с комплексным действующим значением
,
через выходные зажимы – с комплексным действующим значением ![]() .
Заметим, что в роли источника и приемника электрической энергии могут выступать
другие четырехполюсники.
.
Заметим, что в роли источника и приемника электрической энергии могут выступать
другие четырехполюсники.
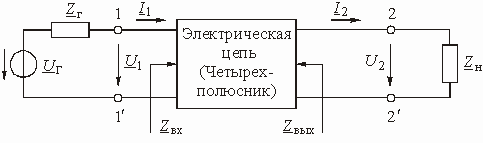
Рис. 1.1
На рис. 1.1 использованы символические обозначения напряжений и токов. Это означает, что анализ электрической цепи проводится для гармонического колебания определенной частоты. Для данного гармонического колебания можно определить передаточную функцию нагруженного четырехполюсника, которая будет представлять собой отношение комплексного действующего значения выходной электрической величины к комплексному действующему значению входной электрической величины.
Если входным воздействием считать
напряжение генератора с комплексным действующим значением ![]() ,
а реакцией четырехполюсника на это воздействие – напряжение с комплексным действующим
значением
,
а реакцией четырехполюсника на это воздействие – напряжение с комплексным действующим
значением ![]() или
ток с комплексным действующим значением
или
ток с комплексным действующим значением ![]() ,
то получаются комплексные передаточные функции общего вида:
,
то получаются комплексные передаточные функции общего вида:
![]() , (1.1)
, (1.1)
![]() . (1.2)
. (1.2)
В частных случаях, когда заданными воздействиями являются напряжение на входных зажимах четырехполюсника или ток, протекающий через эти зажимы, получают следующие четыре разновидности передаточных функций:
![]() –
комплексный коэффициент передачи по напряжению (для активных четырехполюсников,
например усилителей, он носит название коэффициента усиления по напряжению);
–
комплексный коэффициент передачи по напряжению (для активных четырехполюсников,
например усилителей, он носит название коэффициента усиления по напряжению);
![]() –
комплексный коэффициент передачи по току (для активных цепей – коэффициент усиления
по току);
–
комплексный коэффициент передачи по току (для активных цепей – коэффициент усиления
по току);
![]() –
комплексное передаточное сопротивление;
–
комплексное передаточное сопротивление;
![]() –
комплексная передаточная проводимость.
–
комплексная передаточная проводимость.
Часто в теории цепей используют нормированную или рабочую передаточную функцию четырехполюсника:
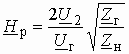 , (1.3)
, (1.3)
которая получается путем нормирования
(1.1) множителем  .
.

Как всякую комплексную величину Н можно представить в показательной форме:
![]() , (1.4)
, (1.4)
где ![]() –
модуль комплексной передаточной функции, а j – ее аргумент.
–
модуль комплексной передаточной функции, а j – ее аргумент.
Рассмотрим комплексную передаточную функцию по напряжению
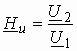 , (1.5)
, (1.5)
Подставляя в (1.5) запись комплексных действующих значений
![]() ,
,
получим
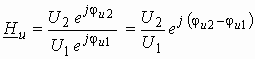 .
.
Из сравнения этого выражения с (1.4) видно, что
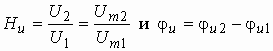 ,
,
т. е. модуль комплексной передаточной функции по напряжению (или комплексного коэффициента усиления по напряжению) показывает во сколько раз изменяется действующее значение (амплитуда) гармонического колебания напряжения на выходе цепи по сравнению с аналогичным значением на входе цепи, а аргумент этой функции определяет сдвиг фаз между гармоническими колебаниями напряжения на входе и выходе.
Точно так же можно найти:
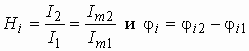 .
.
Все сказанное выше о коэффициенте передачи по напряжению справедливо и для коэффициента передачи по току.

Если мы будем изменять частоту гармонического колебания, то выражение (1.4) следует записать в виде:
![]() . (1.6)
. (1.6)
Функция частоты ![]() называется
амплитудно-частотной характеристикой цепи (АЧХ). Она показывает какие
изменения в амплитуды гармонических колебаний вносит цепь на каждой частоте.
называется
амплитудно-частотной характеристикой цепи (АЧХ). Она показывает какие
изменения в амплитуды гармонических колебаний вносит цепь на каждой частоте.
Функция частоты ![]() называется
фазо-частотной характеристикой цепи (ФЧХ). Соответственно эта характеристика
показывает какой фазовый сдвиг приобретает гармоническое колебание каждой частоты
при распространении по цепи.
называется
фазо-частотной характеристикой цепи (ФЧХ). Соответственно эта характеристика
показывает какой фазовый сдвиг приобретает гармоническое колебание каждой частоты
при распространении по цепи.
Комплексную передаточную функцию
![]() можно представить
также в алгебраической форме:
можно представить
также в алгебраической форме:
![]() ,
,
где Re и Im означают реальную и мнимую части комплексной величины.
Из теории комплексных величин известно, что
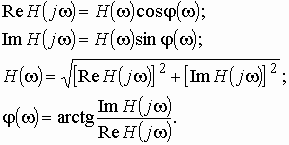
АЧХ и ФЧХ цепи можно представить
единым графиком, если построить зависимость комплексной передаточной функции
![]() от частоты
w на комплексной плоскости. При этом конец вектора
от частоты
w на комплексной плоскости. При этом конец вектора ![]() опишет
некоторую кривую, которая называется годографом комплексной передаточной
функции (рис. 1.3).
опишет
некоторую кривую, которая называется годографом комплексной передаточной
функции (рис. 1.3).
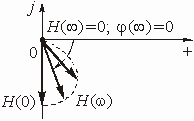
Рис. 1.3

Часто специалисты оперируют понятием логарифмической амплитудно-частотной характеристики (ЛАХ):
![]() .
.
Значения величины К оцениваются в децибелах (дБ). В активных цепях, содержащих усилители, величину К называют еще логарифмическим усилением. Для пассивных цепей вместо коэффициента усиления вводят понятие ослабления цепи:
![]() , (1.7)
, (1.7)
которое также оценивается в децибелах.

Если вместо комплексных сопротивлений
емкости ![]() и индуктивности
и индуктивности
![]() иметь дело
с операторными сопротивлениями емкости
иметь дело
с операторными сопротивлениями емкости ![]() и
индуктивность pL, то в выражении
и
индуктивность pL, то в выражении ![]() нужно
заменить
нужно
заменить ![]() на
р.
на
р.
Операторная передаточная функция
цепи ![]() может
быть записана в общем виде как дробно-рациональная функция с вещественными коэффициентами:
может
быть записана в общем виде как дробно-рациональная функция с вещественными коэффициентами:
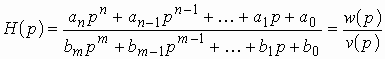 , (1.8)
, (1.8)
или в виде
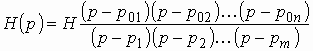 , (1.9)
, (1.9)
где ![]() –
нули;
–
нули; ![]() – полюсы
передаточной функции;
– полюсы
передаточной функции; ![]() .
.
Заменив в (1.8) оператор р на jw , вновь получим комплексную передаточную функцию цепи
![]() ,
,
где АЧХ цепи
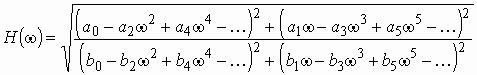 ; (1.10)
; (1.10)
ФЧХ цепи
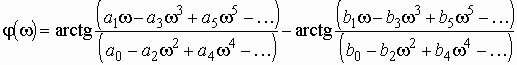 . (1.11)
. (1.11)
Учитывая, что ![]() является
иррациональной функцией, обычно при анализе и синтезе цепей имеют дело с квадратом
АЧХ:
является
иррациональной функцией, обычно при анализе и синтезе цепей имеют дело с квадратом
АЧХ:
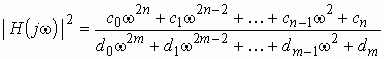 , (1.12)
, (1.12)
где коэффициенты ![]() получаются
путем объединения коэффициентов при одинаковых степенях переменной w .
получаются
путем объединения коэффициентов при одинаковых степенях переменной w .

Перечислим основные свойства операторных передаточных функций и квадрата АЧХ пассивных цепей:
1. Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.
2. Полюсы передаточной функции
располагаются в левой полуплоскости комплексной переменной р. На расположение
нулей ограничений нет. Докажем это свойство на примере передаточной функции
![]() . Выберем
входное воздействие
. Выберем
входное воздействие ![]() или
в операторной форме
или
в операторной форме ![]() .
Изображение выходного напряжения
.
Изображение выходного напряжения ![]() в
этом случае численно равно
в
этом случае численно равно ![]() ,
т. е.
,
т. е.
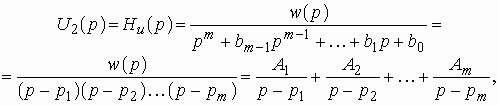
где ![]() –
полином числителя передаточной функции;
–
полином числителя передаточной функции; ![]() –
коэффициенты разложения дробно-рациональной функции на сумму простых дробей.
–
коэффициенты разложения дробно-рациональной функции на сумму простых дробей.
Перейдем от изображения ![]() к
оригиналу
к
оригиналу ![]() :
:
![]() , (1.13)
, (1.13)
где в общем случае ![]() .
.
В пассивных и устойчивых активных
четырехполюсниках колебания на выходе четырехполюсника после прекращения воздействия
должны иметь затухающий характер. Это означает, что в (1.13) вещественные части
полюсов ![]() должны
быть отрицательными
должны
быть отрицательными ![]() ,
т. е. полюсы должны находиться в левой полуплоскости переменной р.
,
т. е. полюсы должны находиться в левой полуплоскости переменной р.
3. Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей, т. е. n Ф m. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимала бы бесконечно большое значение (так как числитель рос бы с увеличением частоты быстрее знаменателя), т. е. цепь обладала бы бесконечным усилением, что противоречит физическому смыслу.
4. Квадрат АЧХ является четной рациональной функцией переменной w с вещественными коэффициентами. Это свойство с очевидностью вытекает из способа получения квадрата АЧХ по передаточной функции.
5. Квадрат АЧХ не может принимать
отрицательных и бесконечно больших значений при w > 0. Неотрицательность
![]() следует из
свойств квадрата модуля комплексной величины. Конечность значений АЧХ на реальных
частотах объясняется так же, как и в свойстве 3.
следует из
свойств квадрата модуля комплексной величины. Конечность значений АЧХ на реальных
частотах объясняется так же, как и в свойстве 3.

В большинстве цепей с зависимыми источниками имеется по крайней мере два пути прохождения сигнала: прямой (от входа к выходу) и обратный (с выхода на вход). Обратный путь прохождения сигнала реализуется с помощью специальной цепи обратной связи (ОС). Таких путей, а значит и цепей ОС, может быть несколько. Наличие в цепях с зависимыми источниками ОС придает им новые ценные качества, которыми не обладают цепи без ОС. Например, с помощью цепей ОС можно осуществить температурную стабилизацию режима работы цепи, уменьшить нелинейные искажения, возникающие в цепях с нелинейными элементами и т. д.
Любую цепь с обратной связью можно представить состоящей из двух четырехполюсников (рис. 1.6).
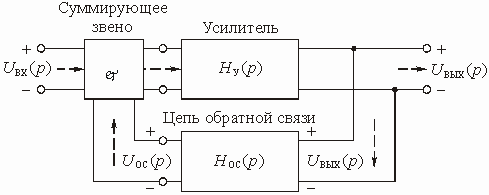
Рис. 1.6
Активный линейный четырехполюсник
с передаточной функцией по напряжению ![]() является
усилителем. Его иногда называют основным элементом цепи и говорят, что он образует
канал прямого усиления.
является
усилителем. Его иногда называют основным элементом цепи и говорят, что он образует
канал прямого усиления.
Пассивный четырехполюсник с передаточной
функцией по напряжению ![]() называется
цепью обратной связи. На входе цепи осуществляется суммирование входного напряжения
называется
цепью обратной связи. На входе цепи осуществляется суммирование входного напряжения
![]() и напряжения
обратной связи
и напряжения
обратной связи ![]() .
.
Выведем формулу передаточной функции
по напряжению цепи, изображенной на рис. 1.6. Пусть на вход подается напряжение
![]() . Его операторное
изображения
. Его операторное
изображения ![]() .
На выходе цепи возникает напряжение
.
На выходе цепи возникает напряжение ![]() .
В соответствии с рис. 1.6 его операторное изображение
.
В соответствии с рис. 1.6 его операторное изображение
![]() . (1.14)
. (1.14)
Операторное изображение ![]() можно
записать через передаточную функцию
можно
записать через передаточную функцию ![]() цепи
обратной связи
цепи
обратной связи
![]() .
.
Тогда выражение (1.14) можно переписать в виде
![]()
или
![]() . (1.15)
. (1.15)
Операторная передаточная функция по напряжению цепи с ОС (см. рис. 1.6).
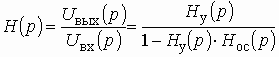 . (1.16)
. (1.16)

Переходя в (1.16) от оператора
р к оператору ![]() ,
получаем комплексную передаточную функцию
,
получаем комплексную передаточную функцию
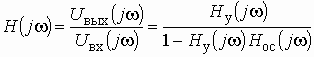 . (1.20)
. (1.20)
Произведение ![]() представляет
собой комплексную передаточную функцию усилителя и цепи обратной связи при условии,
что обратная связь разорвана (рис. 1.10). Функцию
представляет
собой комплексную передаточную функцию усилителя и цепи обратной связи при условии,
что обратная связь разорвана (рис. 1.10). Функцию ![]() называют
передаточной функцией по петле ОС или петлевым усилением. Введем понятия
положительной и отрицательной обратной связи. Эти понятия играют заметную роль
в теории цепей с обратной связью.
называют
передаточной функцией по петле ОС или петлевым усилением. Введем понятия
положительной и отрицательной обратной связи. Эти понятия играют заметную роль
в теории цепей с обратной связью.
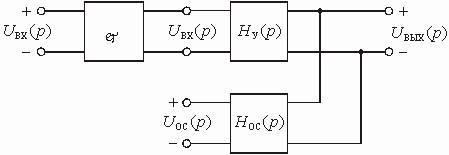
Рис. 1.10
Предположим вначале, что передаточные
функции ![]() ,
, ![]() ,
,
![]() не зависят
от частоты и являются вещественными числами. Такая ситуация возможна, когда
в цепи отсутствуют LC-элементы. При этом
не зависят
от частоты и являются вещественными числами. Такая ситуация возможна, когда
в цепи отсутствуют LC-элементы. При этом ![]() может
быть как положительным, так и отрицательным числом. В первом случае сдвиг фаз
между входным и выходным напряжениями или, другими словами, сдвиг фаз по петле
обратной связи равен нулю или
может
быть как положительным, так и отрицательным числом. В первом случае сдвиг фаз
между входным и выходным напряжениями или, другими словами, сдвиг фаз по петле
обратной связи равен нулю или ![]() ,
k = 0, 1, 2, ... Во втором случае, когда
,
k = 0, 1, 2, ... Во втором случае, когда ![]() ,
сдвиг фаз по этой петле равен
,
сдвиг фаз по этой петле равен ![]() или
или
![]() .
.
Если в цепи с обратной связью сдвиг
фаз по петле равен нулю, то обратная связь называется положительной,
если же сдвиг фаз равен ![]() ,
то такая обратная связь называется отрицательной.
,
то такая обратная связь называется отрицательной.
Передаточную функцию ![]() можно
изобразить в виде векторов и показать их на комплексной плоскости. При положительной
обратной связи вектор
можно
изобразить в виде векторов и показать их на комплексной плоскости. При положительной
обратной связи вектор ![]() находится
на положительной вещественной полуоси, а при отрицательной обратной связи –
на отрицательной вещественной полуоси.
находится
на положительной вещественной полуоси, а при отрицательной обратной связи –
на отрицательной вещественной полуоси.
Кривая, которую описывает конец
вектора ![]() при
изменении частоты w (рис. 1.11), называется, как известно, годографом.
при
изменении частоты w (рис. 1.11), называется, как известно, годографом.
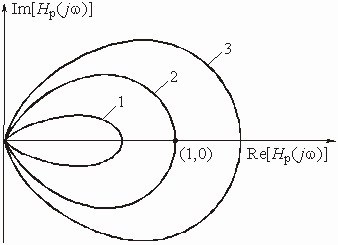
Рис. 1.11
Представление ![]() в
виде годографа позволяет определить вид обратной связи в случае частотнозависимой
обратной связи.
в
виде годографа позволяет определить вид обратной связи в случае частотнозависимой
обратной связи.
Обратная связь называется положительной,
если годограф ![]() лежит
в правой, и отрицательной – если в левой полуплоскости комплексной плоскости.
Отрицательная ОС применяется для стабилизации коэффициента усиления, подавления
паразитных сигналов, коррекции частотных характеристик; положительная ОС может
являться причиной неустойчивости цепи.
лежит
в правой, и отрицательной – если в левой полуплоскости комплексной плоскости.
Отрицательная ОС применяется для стабилизации коэффициента усиления, подавления
паразитных сигналов, коррекции частотных характеристик; положительная ОС может
являться причиной неустойчивости цепи.

Введем понятия устойчивой и неустойчивой цепи. Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Если корни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения. Таким образом, для определения условий устойчивости цепи достаточно найти характеристическое уравнение и его корни. Как видим, условия устойчивости можно определить и не вводя понятие обратной связи. Однако здесь возникает ряд проблем. Дело в том, что вывод характеристического уравнения и определение его корней являются громоздкой процедурой, особенно для цепей высокого порядка. Введение понятия обратной связи облегчает получение характеристического уравнения или даже дает возможность обойтись без него. Крайне важно и то, что понятие обратной связи адекватно физическим процессам, возникающим в цепи, поэтому они становятся более наглядными. Глубокое понимание физических процессов облегчает работу по созданию автогенераторов, усилителей и т. д.
Рассмотрим цепь (см. рис. 1.6)
и выведем ее характеристическое уравнение. Пусть ![]() и,
значит,
и,
значит, ![]() . Тогда
из (1.15) следует:
. Тогда
из (1.15) следует:
![]() . (1.21)
. (1.21)
Здесь ![]() (в
противном случае цепь нельзя считать возбужденной) и поэтому равенство (1.21)
выполняется при условии
(в
противном случае цепь нельзя считать возбужденной) и поэтому равенство (1.21)
выполняется при условии
![]() . (1.22)
. (1.22)
Если записать передаточную функцию
основной цепи в виде ![]()
![]() ,
а цепи ОС –
,
а цепи ОС – ![]() ,
то уравнение (1.22) перепишется следующим образом:
,
то уравнение (1.22) перепишется следующим образом:
![]() .
.
Это равенство выполняется при
![]() . (1.23)
. (1.23)
Выражение в левой части этого равенства является полиномом, поэтому (1.23) можно записать в общем виде:
![]() . (1.24)
. (1.24)
Это и есть характеристическое уравнение цепи.
Корни уравнения (1.24) в общем случае являются комплексными величинами
![]()
где ![]() .
Зная корни характеристического уравнения, можно записать выходное напряжение:
.
Зная корни характеристического уравнения, можно записать выходное напряжение:
![]() . (1.25)
. (1.25)
Чтобы напряжение ![]() не
возрастало безгранично, всем корням
не
возрастало безгранично, всем корням ![]() характеристического
уравнения необходимо иметь отрицательные вещественные части, т. е. корни должны
располагаться в левой полуплоскости комплексной переменной
характеристического
уравнения необходимо иметь отрицательные вещественные части, т. е. корни должны
располагаться в левой полуплоскости комплексной переменной ![]() .
Цепь с ОС, обладающая такими свойствами, называется абсолютно устойчивой.
.
Цепь с ОС, обладающая такими свойствами, называется абсолютно устойчивой.
При исследовании цепей с обратной
связью могут возникать две проблемы. Если проектируемая цепь должна быть устойчивой,
то необходимо располагать критерием, который по виду функций ![]() и
и
![]() позволял бы
судить об отсутствии корней характеристического уравнения в правой полуплоскости
р. Если обратная связь используется для создания неустойчивой автоколебательной
цепи, то следует убедиться, что корни уравнения (1.24) расположены, наоборот,
в правой полуплоскости. При этом необходимо иметь такое расположение корней,
при котором самовозбуждение происходило бы на требуемой частоте.
позволял бы
судить об отсутствии корней характеристического уравнения в правой полуплоскости
р. Если обратная связь используется для создания неустойчивой автоколебательной
цепи, то следует убедиться, что корни уравнения (1.24) расположены, наоборот,
в правой полуплоскости. При этом необходимо иметь такое расположение корней,
при котором самовозбуждение происходило бы на требуемой частоте.
Рассмотрим критерий устойчивости цепи, названный критерием Найквиста, и позволяющий судить об устойчивости цепи с обратной связью по свойствам разомкнутой цепи (рис. 1.10).
Передаточная функция разомкнутой
цепи, или петлевое усиление, ![]() входит
в характеристическое уравнение (1.22):
входит
в характеристическое уравнение (1.22):
![]() , (1.26)
, (1.26)
Если найдется такая частота w ,
для которой конец вектора ![]() попадает
в точку с координатами (1, j0), то это будет означать, что выполняется
условие (1.26), т. е. на этой частоте в цепи произойдет самовозбуждение. Значит,
по годографу можно определить, устойчива цепь или нет. Для этого используется
критерий Найквиста, который формулируется следующим образом: если годограф
передаточной функции разомкнутой цепи не охватывает точку с координатами (1, j0),
то при замкнутой цепи обратной связи цепь является устойчивой. В том
случае, когда годограф
попадает
в точку с координатами (1, j0), то это будет означать, что выполняется
условие (1.26), т. е. на этой частоте в цепи произойдет самовозбуждение. Значит,
по годографу можно определить, устойчива цепь или нет. Для этого используется
критерий Найквиста, который формулируется следующим образом: если годограф
передаточной функции разомкнутой цепи не охватывает точку с координатами (1, j0),
то при замкнутой цепи обратной связи цепь является устойчивой. В том
случае, когда годограф ![]() охватывает
точку (1, j0), цепь неустойчива. На рис. 1.11 показаны годографы трех
цепей с положительной обратной связью (цифра 1 соответствует годографу устойчивой
цепи).
охватывает
точку (1, j0), цепь неустойчива. На рис. 1.11 показаны годографы трех
цепей с положительной обратной связью (цифра 1 соответствует годографу устойчивой
цепи).
Пользуясь критерием Найквиста,
легко получить условия самовозбуждения цепи с ОС. Запишем выражение для ![]() в
виде
в
виде
![]() ,
,
где ![]() ,
,
![]() – модули передаточных
функций;
– модули передаточных
функций;
![]() ,
,
![]() –
фазовые сдвиги соответственно в основном элементе и в цепи ОС.
–
фазовые сдвиги соответственно в основном элементе и в цепи ОС.
Условия пересечения годографом
оси абсцисс ![]() при
при
![]() Х 1 можно записать
в виде двух условий:
Х 1 можно записать
в виде двух условий:
- условие (уравнение) баланса фаз
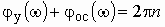 ,
где n = 0, 1, 2, ...;
,
где n = 0, 1, 2, ...; - амплитудное условие
![]() Х
1, или
Х
1, или ![]() Х 1.
Х 1.
Выполнение неравенства соответствует
режиму возникновения колебаний с нарастающей амплитудой, что характерно для
начального этапа самовозбуждения. Выполнение равенства ![]() соответствует
режиму генерации гармонического напряжения на частоте с постоянной амплитудой
и носит название баланса амплитуд.
соответствует
режиму генерации гармонического напряжения на частоте с постоянной амплитудой
и носит название баланса амплитуд.
Как будет показано ниже, уравнение баланса фаз
позволяет определить частоту, на которой происходит самовозбуждение цепи с ОС,
а уравнение баланса амплитуд дает возможность определить величину амплитуды
![]() генерируемого
колебания с частотой
генерируемого
колебания с частотой ![]() в
стационарной режиме.
в
стационарной режиме.
Примеры к главе 1
Пример 1.1
Определить коэффициент передачи
по напряжению ![]() ,
АЧХ и ФЧХ цепи, изображенной на рис. 1.2, а.
,
АЧХ и ФЧХ цепи, изображенной на рис. 1.2, а.
Согласно (1.5) запишем
![]() .
.
Найдем комплексную функцию ![]() на
выходе цепи:
на
выходе цепи:
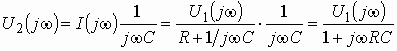 .
.
Подставив ![]() в
формулу для
в
формулу для ![]() ,
получим комплексную передаточную функцию:
,
получим комплексную передаточную функцию:
![]() ;
;
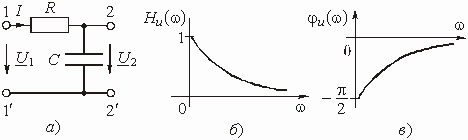
Рис. 1.2
АЧХ цепи
![]() ;
;
ФЧХ цепи
![]() .
.
Изменяя частоту w от 0 до Ґ , можем изобразить графики АЧХ и ФЧХ цепи (рис. 1.2, б и в).
Пример 1.2
Известно, что модуль коэффициента передачи по напряжению цепи принимает следующие значения:
f = 0 кГц Н(f) = 1
f = 1 кГц Н(f) = 0,3
f = 2 кГц Н(f) = 0,01
f = 4 кГц Н(f) = 0,001
f = 8 кГц Н(f) = 0,0001
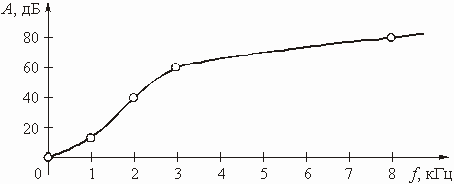
Рис. 1.4
Изобразить график ослабления цепи.
Значения ослабления цепи, рассчитанные по (1.7), приведены в таблице:
|
f, кГц |
0 |
1 |
2 |
4 |
8 |
|
А(f), дБ |
0 |
12 |
40 |
60 |
80 |
График А(f) приведен на рис. 1.4.
Пример 1.3
Найти коэффициент передачи по напряжению и квадрат АЧХ цепи, изображенной на рис. 1.5, а.
Коэффициент передачи по напряжению этой цепи равен
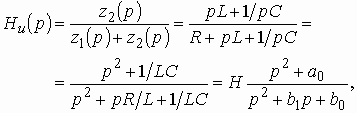
где Н = 1, ![]() ,
,
![]() .
.
Корни числителя этой рациональной дроби, т. е. нули передаточной функции,
![]() .
.
Корни знаменателя, или полюсы передаточной функции,
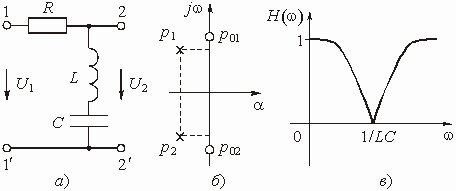
Рис. 1.5
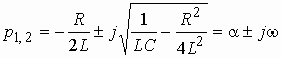 .
.
На рис. 1.5, б показано
расположение нулей и полюсов функции при ![]() .
.
По теореме Виета
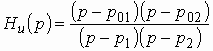 .
.
Амплитудно-частотная характеристика
определяется из ![]() путем
замены р на
путем
замены р на ![]() и
вычисления модуля полученной функции
и
вычисления модуля полученной функции
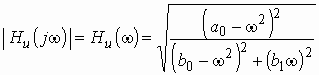 .
.
Квадрат АЧХ запишется в виде
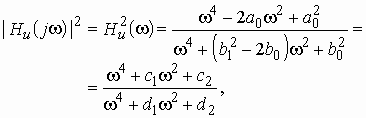
где ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
АЧХ цепи ![]() изображена
на рис. 1.5, в.
изображена
на рис. 1.5, в.
Пример 1.4
На рис. 1.7 изображена цепь на операционном усилителе (ОУ), предназначенная для масштабирования напряжения. Найти передаточную функцию этой цепи.
Получим передаточную функцию этой цепи как цепи с обратной связью, используя формулу (1.16).
Цепью обратной связи на схеме рис.
1.7 служит Г-образный делитель напряжения, составленный из резистивных сопротивлений
![]() и
и ![]() .
Выходное напряжение усилителя
.
Выходное напряжение усилителя ![]() поступает
на вход цепи ОС; напряжение ОС
поступает
на вход цепи ОС; напряжение ОС ![]() снимается
с резистора
снимается
с резистора ![]() .
Передаточная функция по напряжению цепи ОС
.
Передаточная функция по напряжению цепи ОС
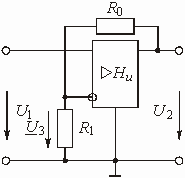
Рис. 1.7
![]() .
.
Воспользуемся формулой (1.16) и
учтем, что входное напряжение ![]() и
напряжение обратной связи
и
напряжение обратной связи ![]() не
суммируются, а вычитаются. Тогда получим передаточную функцию масштабного усилителя:
не
суммируются, а вычитаются. Тогда получим передаточную функцию масштабного усилителя:
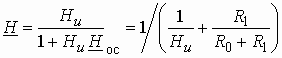 .
.
Учитывая, что в реальных ОУ значение
![]() >> 1, окончательно имеем:
>> 1, окончательно имеем:
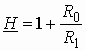 ,
,
Пример 1.5
Звено на ОУ с частотно-зависимой ОС представлено на рис. 1.8. Найти передаточную функцию этого звена.
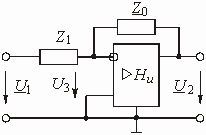
Рис. 1.8
Чтобы проанализировать прямой путь
прохождения сигнала и путь прохождения сигнала ОС, необходимо воспользоваться
методом наложения. Для этого следует поочередно исключать источники входного
напряжения и напряжения обратной связи, заменяя их внутренним сопротивлением.
В случае идеальных источников напряжения их внутреннее сопротивление равно нулю.
Напряжение ![]() ,
приложенное к звену, ослабляется входной цепью, представляющей собой Г-образный
делитель напряжения с сопротивлениями
,
приложенное к звену, ослабляется входной цепью, представляющей собой Г-образный
делитель напряжения с сопротивлениями ![]() и
и
![]() в плечах. Передаточная
функция по напряжению такого делителя равна
в плечах. Передаточная
функция по напряжению такого делителя равна
![]() .
.
Цепь обратной связи также является Г-образным четырехполюсником с передаточной функцией.
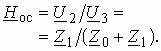
Коэффициент усиления ОУ ![]() .
.
В соответствии с формулой (1.16) получаем передаточную функцию звена:
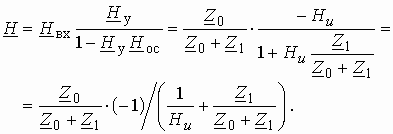
Учитывая, что ![]() >>
1, получаем:
>>
1, получаем:
![]() .
.
Данное звено может выполнять различные
функции в зависимости от вида сопротивлений ![]() и
и
![]() . При
. При ![]() и
и
![]() звено превращается
в инвертирующий масштабный усилитель; при
звено превращается
в инвертирующий масштабный усилитель; при ![]() и
и
![]() – в интегратор;
при
– в интегратор;
при ![]() и
и ![]() –
в дифференциатор.
–
в дифференциатор.
Пример 1.6
Звено второго порядка с регулируемым коэффициентом усиления представлено на рис. 1.9, а. Найти передаточную функцию этого звена.
Анализ прохождения входного сигнала и сигнала в цепи ОС показывает, что звено имеет входную цепь, изображенную на рис. 1.9, б и цепь ОС, показанную на рис. 1.9, в. Передаточные функции этих цепей можно получить матричным методом, например, рассматривая каждую цепь как каскадное соединение соответствующих Г-образных четырехполюсников.
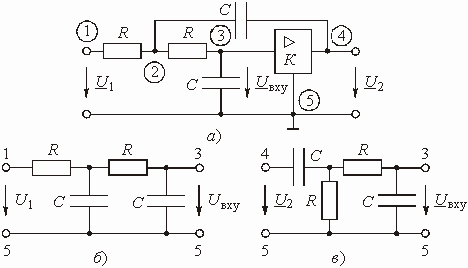
Рис. 1.9
Для входной цепи
![]() . (1.17)
. (1.17)
Для цепи ОС
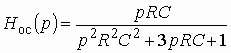 . (1.18)
. (1.18)
С учетом (1.16) получим передаточную функцию звена
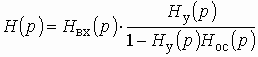 . (1.19)
. (1.19)
Коэффициент передачи усилителя
![]() . Тогда, подставляя
(1.17) и (1.18) в (1.19), после преобразования имеем
. Тогда, подставляя
(1.17) и (1.18) в (1.19), после преобразования имеем
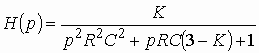 .
.
Пример 1.7
Исследуем устойчивость цепи, изображенной
на рис. 1.9, а. В ней можно выделить усилительный элемент с передаточной
функцией ![]() и
цепь обратной связи (рис. 1.9, в) с передаточной функцией (1.18)
и
цепь обратной связи (рис. 1.9, в) с передаточной функцией (1.18)
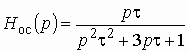 ,
,
где ![]() .
.
Кроме того, напомним, что на усилитель сигнал поступает через входную цепь (рис. 1.9, б), передаточная функция которой (см. (1.17))
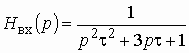 .
.
Получим характеристическое уравнение цепи:
![]()
или
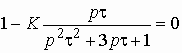 .
.
Откуда окончательно получаем
![]() .
.
Корни этого характеристического уравнения
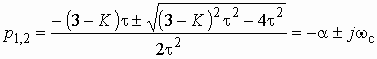
зависят от коэффициента усиления
усилителя К. Расположение корней ![]() и
и
![]() на плоскости
комплексного переменного р для разных коэффициентов усиления и соответствующие
этому графики свободных колебаний в цепи показаны на рис. 1.12.
на плоскости
комплексного переменного р для разных коэффициентов усиления и соответствующие
этому графики свободных колебаний в цепи показаны на рис. 1.12.
Устойчивость данной цепи можно исследовать и с помощью критерия Найквиста. Комплексная передаточная функция разомкнутой цепи равна
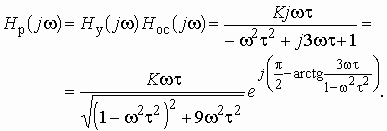
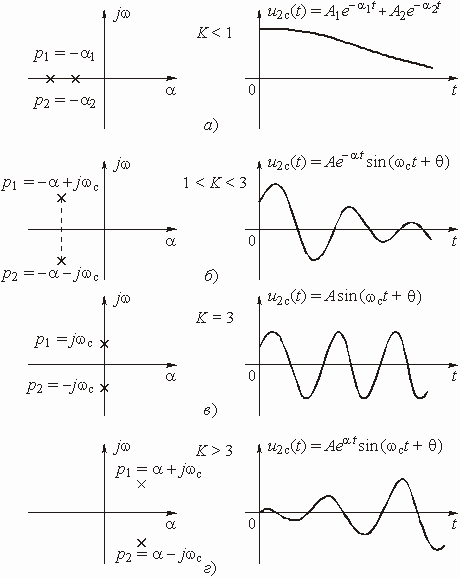
Рис. 1.12
На рис. 1.11 приведены годографы
![]() устойчивой
(К = 2, кривая 1) и неустойчивой (К = 3, кривая 2; К = 4,
кривая 3) цепи.
устойчивой
(К = 2, кривая 1) и неустойчивой (К = 3, кривая 2; К = 4,
кривая 3) цепи.
Вопросы и задания для самопроверки
1. Что такое комплексная передаточная функция? Какие виды комплексных передаточных функций четырехполюсника известны?
2. Определить коэффициент
передачи по напряжению ![]() , АЧХ
и ФЧХ цепи, изображенной на рис. 1.2, а, если выходным напряжением является напряжение
на резисторе
R. Построить графики АЧХ и ФЧХ.
, АЧХ
и ФЧХ цепи, изображенной на рис. 1.2, а, если выходным напряжением является напряжение
на резисторе
R. Построить графики АЧХ и ФЧХ.
Ответ: 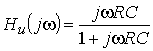 ;
;
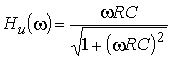 ;
;
![]() 90° – w
RC.
90° – w
RC.
3. Определить коэффициент передачи по напряжению при холостом ходе и коэффициент передачи по току при коротком замыкании для П-образного четырехполюсника в продольную ветвь которого включена индуктивность L, а в поперечные ветви – емкость С.
Ответ: 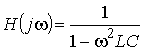 .
.
4. Определить ослабление,
вносимое цепью рис. 1.2, а, при
R = 31,8 кОм и ![]() =
10 кОм.
=
10 кОм.
Ответ: 12 дБ.
5. Что такое операторная передаточная функция? Как она связана с комплексной передаточной функцией? Как определить нули и полюсы операторной передаточной функции?
6. Определить операторную
передаточную функцию, комплексный коэффициент передачи по напряжению, АЧХ
и квадрат АЧХ последовательного колебательного контура, изображенного на рис.
1.5, а, если выходным напряжением
![]() является
напряжение на емкости С. Построить
график АЧХ цепи.
является
напряжение на емкости С. Построить
график АЧХ цепи.
Ответ:
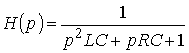 ;
;
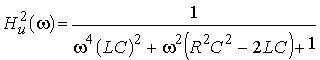 .
.
7. Перечислить основные свойства операторных передаточных функций пассивных цепей.
8. Как рассчитывается передаточная функция цепи с обратной связью?
9. Доказать, что операторная передаточная функция дифференциатора на операционном усилителе равна (– pRC). Построить график АЧХ такого дифференциатора.
10. Рассчитать передаточную функцию каскадного соединения цепей, изображенных на рис. 1.2, а и 1.7. Построить график АЧХ полученной цепи.
11. Определить передаточную функцию фильтра, изображенного на рис. 1.13.
|
Рис. 1.13 |
Ответ:
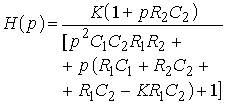 .
.
12. Что такое годограф петлевого усиления? Как по годографу определить тип обратной связи?
14. Определить комплексную
передаточную функцию ![]() разомкнутой
цепи, изображенной на рис. 1.13. Исследуйте зависимость устойчивости цепи
от величины коэффициента усиления К.
разомкнутой
цепи, изображенной на рис. 1.13. Исследуйте зависимость устойчивости цепи
от величины коэффициента усиления К.
Ответ: 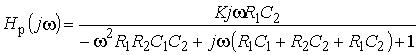 .
.
Глава 2. Электрические фильтры

Полоса частот, в которой ослабление мало, называется полосой пропускания. Полоса частот, в которой ослабление велико, называется полосой непропускания (задерживания). Между этими полосами находится переходная область.
По расположению полосы пропускания на шкале частот различают следующие фильтры:
нижних частот (ФНЧ), в которых
полоса пропускания располагается на шкале частот от w = 0 до некоторой граничной
частоты ![]() , а
полоса непропускания (задерживания) – от частоты
, а
полоса непропускания (задерживания) – от частоты ![]() до
бесконечно больших частот (рис. 2.1, а);
до
бесконечно больших частот (рис. 2.1, а);
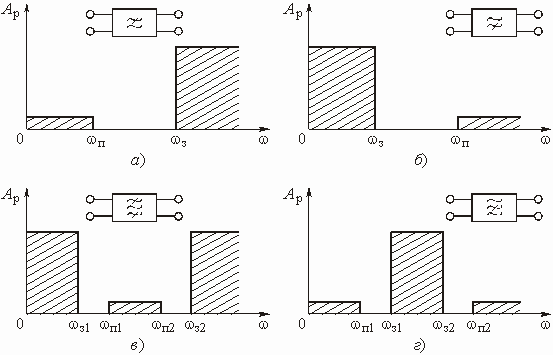
Рис. 2.1
верхних частот (ФВЧ) с полосой
пропускания от частоты ![]() до
бесконечно больших частот и полосой непропускания от частоты w = 0 до
до
бесконечно больших частот и полосой непропускания от частоты w = 0 до ![]() (рис.
2.1, б);
(рис.
2.1, б);
полосовые (ПФ), в которых полоса
пропускания ![]() располагается
между полосами непропускания
располагается
между полосами непропускания ![]() и
и
![]() (рис. 2.1,
в);
(рис. 2.1,
в);
заграждающие (режекторные) (ЗФ
или РФ), в которых между полосами пропускания ![]() и
и
![]() находится полоса
непропускания
находится полоса
непропускания ![]() (рис.
2.1, г);
(рис.
2.1, г);
многополосные, имеющие несколько полос пропускания.
На рис. 2.1, а – г показаны также условные обозначения фильтров каждого типа в соответствии с ГОСТ.
В соответствии с используемой элементной базой к настоящему моменту выделились несколько классов фильтров. Исторически первыми (и все еще наиболее широко применяемыми) являются пассивные фильтры, содержащие элементы L и С. Они носят название LC-фильтров.
Во многих случаях на практике требовалась крайне высокая избирательность (различие ослаблений в полосах пропускания и непропускания в десятки тысяч раз). Это привело к появлению фильтров с механическими резонаторами: кварцевых, магнитострикционных, электромеханических.
По-видимому, самые значительные достижения в области теории и проектирования фильтров связаны с успехами микроэлектроники. Требования микроминиатюризации радиоэлектронной аппаратуры заставили отказаться от использования индуктивностей, которые имеют большие габаритные размеры, особенно на низких частотах, и не поддаются исполнению в микроминиатюрном виде. Появились активные RC-фильтры, состоящие из резисторов, конденсаторов и активных приборов (например, транзисторов). Эти фильтры могут быть выполнены в виде микромодульной конструкции или интегральной схемы. Применение активных RC-фильтров ограничивается пока сравнительно небольшим диапазоном частот до десятков (иногда сотен) килогерц.
Разработка цифровых систем связи и достижения в области цифровых вычислительных машин стимулировали создание фильтров на базе элементов цифровой и вычислительной техники – цифровых фильтров. В силу специфики элементной базы фильтров не будем далее упоминать о них, хотя расчет таких фильтров производится методами теории электрических цепей. Заинтересованные читатели могут обратиться к специальной литературе по цифровым фильтрам.

В идеальном случае (идеальный фильтр)
характеристика рабочего ослабления, например для ФНЧ, имеет вид, показанный
на рис. 2.2, а. С рабочим ослаблением связана рабочая амплитудно-частотная
характеристика (АЧХ): ![]() .
На рис. 2.2, б изображена АЧХ идеального фильтра нижних частот.
.
На рис. 2.2, б изображена АЧХ идеального фильтра нижних частот.
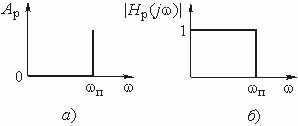
Рис. 2.2
Реальные фильтры (т. е. фильтры, состоящие из реальных элементов) имеют характеристики рабочего ослабления и амплитудно-частотную, отличные от идеальных.
Требования к электрическим характеристикам
фильтров задаются в виде допустимых пределов изменения этих характеристик. Так,
рабочее ослабление в полосе пропускания не должно превышать некоторого максимального
допустимого значения ![]() ,
а в полосе непропускания не должно быть ниже некоторого минимально допустимого
значения
,
а в полосе непропускания не должно быть ниже некоторого минимально допустимого
значения ![]() .
Нетрудно изобразить эти требования графически, как это сделано на рис. 2.3,
а. На этом рисунке
.
Нетрудно изобразить эти требования графически, как это сделано на рис. 2.3,
а. На этом рисунке ![]() и
и
![]() – граничные
частоты полос пропускания и непропускания.
– граничные
частоты полос пропускания и непропускания.
Рис. 2.3
Зная требования к ![]() ,
можно пересчитать их в требования к АЧХ или, как это принято в теории фильтров,
в требования к квадрату АЧХ (рис. 2.3, б):
,
можно пересчитать их в требования к АЧХ или, как это принято в теории фильтров,
в требования к квадрату АЧХ (рис. 2.3, б):
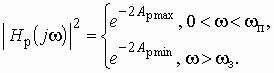
Характеристики проектируемых фильтров должны “укладываться” в эти требования (рис. 2.3, а и б).
Помимо требований к частотной зависимости рабочего ослабления (а значит, и к АЧХ) могут задаваться также требования к фазочастотной характеристике фильтра (скажем, допустимые отклонения от линейного закона) и величине нелинейных искажений (обусловленных, например, наличием железа в катушках индуктивности). Могут предъявляться требования и к другим характеристикам и параметрам фильтра. Ниже будем учитывать только требования к рабочему ослаблению и АЧХ.
Идеальные частотные характеристики фильтра (см. рис. 2.2, а) заведомо нереализуемы. Частотные характеристики реальных фильтров могут лишь приближаться к ним с той или иной степенью точности в зависимости от сложности схемы фильтра.

В общем виде электрические фильтры описываются передаточной функцией вида (1.8)
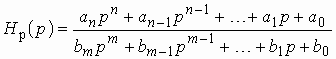 . (2.1)
. (2.1)
Квадрат амплитудно-частотной характеристики таких фильтров (см. (1.12))
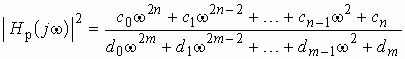 (2.2)
(2.2)
и, следовательно, рабочее ослабление
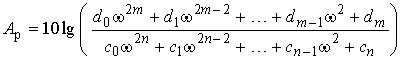 (2.3)
(2.3)
могут при надлежащем выборе степени
полинома (порядка фильтра) и коэффициентов ![]() удовлетворить
заданным требования (см. рис. 2.3).
удовлетворить
заданным требования (см. рис. 2.3).
В теории фильтров принято иметь
дело не с обычной угловой частотой w , а с нормированной частотой ![]() ,
где
,
где ![]() – нормирующая
частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы
пропускания
– нормирующая
частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы
пропускания ![]() ,
так что
,
так что ![]() .
.
В теории электрических фильтров вместо формул (2.2) и (2.3) используют другие, также универсальные для любого типа фильтра:
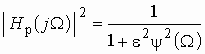 ; (2.4)
; (2.4)
![]() . (2.5)
. (2.5)
Функция ![]() называется
функцией фильтрации. В общем случае – это дробно-рациональная функция с
вещественными коэффициентами (в частности полином), удовлетворяющая условиям:
–1 Ф
называется
функцией фильтрации. В общем случае – это дробно-рациональная функция с
вещественными коэффициентами (в частности полином), удовлетворяющая условиям:
–1 Ф ![]() Ф 1 в
полосе пропускания и
Ф 1 в
полосе пропускания и ![]() .
1 в полосе непропускания фильтра.
.
1 в полосе непропускания фильтра.
В зависимости от вида функции фильтрации
получают различные типы фильтров. Если в качестве функции фильтрации используют
полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров
широкое использование нашли фильтры Баттерворта и Чебышева. Если ![]() –
дробно-рациональная функция (1.8), например, дробь Золотарева, то получают фильтр
Золотарева. Все эти три типа фильтров будут рассмотрены в этой главе.
–
дробно-рациональная функция (1.8), например, дробь Золотарева, то получают фильтр
Золотарева. Все эти три типа фильтров будут рассмотрены в этой главе.

Следует отметить, что имеет смысл
подробно изучать только фильтры нижних частот, т.к. другие типы фильтров (верхних
частот, полосовые и заграждающие) могут быть легко получены из ФНЧ с помощью
замены переменной (частоты). Для этого во всех выражениях, содержащих переменную
W , нужно произвести замену переменной таким образом, чтобы характеристики ФНЧ
(![]() и
и ![]() )
перешли в характеристики соответствующего фильтра. Подобная замена переменной
W называется преобразованием частоты, а исходный ФНЧ – фильтром НЧ-прототипа.
)
перешли в характеристики соответствующего фильтра. Подобная замена переменной
W называется преобразованием частоты, а исходный ФНЧ – фильтром НЧ-прототипа.
Преобразование частоты позволяет установить соответствие между частотами полос пропускания и непропускания НЧ-прототипа и частотами фильтра верхних частот (полосового или заграждающего), а также преобразовать схему ФНЧ в схему ФВЧ (ПФ или ЗФ). Более подробно вопросы, связанные с преобразованием частоты, будут рассматриваться в этой главе.

Если в выражениях, описывающих
квадрат АЧХ фильтра (2.4) и его рабочее ослабление (2.5), в качестве функции
фильтрации используются полиномы Баттерворта ![]() (по
имени автора, предложившего использовать их для “конструирования” частотных
характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.
(по
имени автора, предложившего использовать их для “конструирования” частотных
характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.
Из формул (2.4) и (2.5) следует, что для фильтров Баттерворта на частоте W = 0 значение квадрата АЧХ равно единице, а рабочего ослабления – нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (2.4) и (2.5) приближенно воспроизводят характеристики идеального фильтра.
Чтобы эти характеристики “вписывались”
в предъявляемые к фильтру требования (см. рис. 2.3), необходимо иметь рабочее
ослабление (2.5) в полосе пропускания меньшее ![]() ,
а в полосе непропускания большее
,
а в полосе непропускания большее ![]() .
Первому условию можно удовлетворить, если потребовать на граничной частоте полосы
пропускания (W = 1) выполнения равенства
.
Первому условию можно удовлетворить, если потребовать на граничной частоте полосы
пропускания (W = 1) выполнения равенства ![]() или
или
![]() . Отсюда с
учетом (2.5) или (2.4) имеем
. Отсюда с
учетом (2.5) или (2.4) имеем ![]() и
и
![]() . Вычисленный
таким способом коэффициент e
. Вычисленный
таким способом коэффициент e
![]() (2.6)
(2.6)
называется коэффициентом неравномерности ослабления в полосе пропускания фильтра.
В формуле (2.6) величина ![]() имеет
размерность непер. Если воспользоваться значениями
имеет
размерность непер. Если воспользоваться значениями ![]() в
децибелах, то
в
децибелах, то
![]() . (2.7)
. (2.7)
С учетом введенных обозначений квадрат АЧХ фильтра Баттерворта запишется в виде
![]() . (2.8)
. (2.8)
Эта функция удовлетворяет свойствам квадрата АЧХ реальных четырехполюсников, и поэтому ей можно сопоставить физически осуществимый электрический фильтр.
Рабочее ослабление фильтра Баттерворта:
![]() . (2.9)
. (2.9)
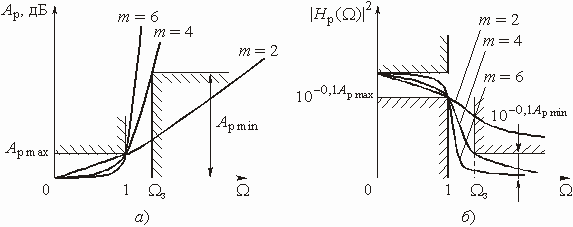
Рис. 2.4
Крутизна частотных характеристик
(2.8) и (2.9) зависит от степени m (порядка фильтра).Чем больше степень
m, тем выше крутизна характеристик. На рис.2.4, а, и б
показаны графики рабочего ослабления и квадрата АЧХ фильтра Баттерворта для
различных m. Таким образом, для удовлетворения требований в полосе непропускания
необходимо выбрать соответствующий порядок фильтра m. Его легко определить
из условия: на граничной частоте полосы непропускания ![]()
![]() Х
Х
![]() или
или ![]() Ф
Ф
![]() . С учетом
этого условия получим 1 +
. С учетом
этого условия получим 1 + ![]() >
>
![]() , откуда
, откуда ![]() Х
Х
![]() . Логарифмируя
обе части неравенства, придем к выражению
. Логарифмируя
обе части неравенства, придем к выражению
![]() Х
Х
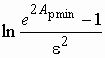 .
.
Из него находим окончательно
![]() Х
Х
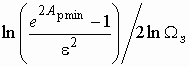 . (2.10)
. (2.10)
Величина ![]() входит
в формулу в неперах. Если вычислять ее в децибелах, то
входит
в формулу в неперах. Если вычислять ее в децибелах, то
![]() Х
Х
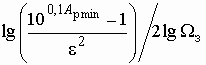 . (2.11)
. (2.11)
Передаточную функцию фильтра Баттерворта
можно получить из (2.8), если положить ![]() :
:
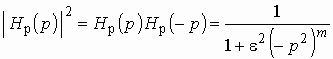 . (2.12)
. (2.12)
и разложить знаменатель полученной функции на произведение сомножителей.
Вычислим корни знаменателя, т.
е. полюсы функции ![]() ,
отдельно для четных и нечетных значений m. Для четных значений m
,
отдельно для четных и нечетных значений m. Для четных значений m
![]() и
и
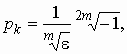 k =
1, 2, ..., 2m.
k =
1, 2, ..., 2m.
Так как
![]() ,
,
имеем
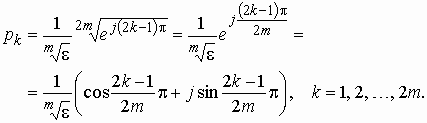 (2.13)
(2.13)
Для нечетных значений m
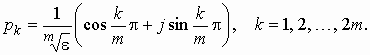
Выражение (2.12) примет вид
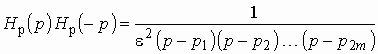 .
.
Половина полюсов функции ![]() лежит
в левой полуплоскости комплексной переменной p и может быть отнесена
к передаточной функции реализуемого фильтра
лежит
в левой полуплоскости комплексной переменной p и может быть отнесена
к передаточной функции реализуемого фильтра ![]() .
Другая половина полюсов, являясь зеркальным отражением первой, располагается
в правой полуплоскости и относится к
.
Другая половина полюсов, являясь зеркальным отражением первой, располагается
в правой полуплоскости и относится к ![]() .
.
Построенная из полюсов, лежащих в левой полуплоскости, передаточная функция фильтра Баттерворта является полиномиальной передаточной функцией типа (2.1):
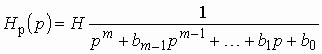 ,
,
где ![]() .
.
Используя введенное ранее обозначение
![]() полинома Баттерворта,
можно представить частотные характеристики (2.8) и (2.9) фильтра Баттерворта
в следующей форме:
полинома Баттерворта,
можно представить частотные характеристики (2.8) и (2.9) фильтра Баттерворта
в следующей форме:
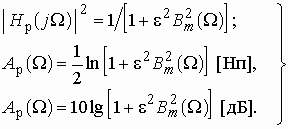 (2.14)
(2.14)
Фильтры Баттерворта называют также фильтрами с максимально плоским ослаблением в полосе пропускания (см. рис. 2.4, а).

Если в качестве функции фильтрации
в (2.4) и (2.5) использовать полином Чебышева, обозначаемый ![]() ,
то формулы (2.14) примут вид:
,
то формулы (2.14) примут вид:
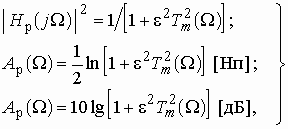 (2.15)
(2.15)
где ![]() –
полином Чебышева степени (порядка) m; e – коэффициент неравномерности,
определяемый (2.6) или (2.7).
–
полином Чебышева степени (порядка) m; e – коэффициент неравномерности,
определяемый (2.6) или (2.7).
Фильтры с частотными характеристиками
(2.15) называются фильтрами Чебышева. Проанализируем частотные характеристики
фильтра Чебышева. Для этого вначале рассмотрим свойства полиномов ![]() .
Ниже приведены шесть первых полиномов Чебышева:
.
Ниже приведены шесть первых полиномов Чебышева:
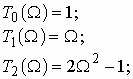
 (2.16а)
(2.16а)
Любой полином Чебышева при m
Х 2 может быть вычислен по рекуррентной формуле ![]() .
Таким образом, выражения (2.15) удовлетворяют общим выражениям (2.1) – (2.3)
характеристик полиномиальных фильтров.
.
Таким образом, выражения (2.15) удовлетворяют общим выражениям (2.1) – (2.3)
характеристик полиномиальных фильтров.
Существует единая тригонометрическая форма записи полиномов Чебышева в интервале –1 Ф W Ф 1:
![]() . (2.16б)
. (2.16б)
Действительно, ![]() ;
;
![]() ;
; ![]() .
Вне интервала –1 Ф Ф W Ф 1 полиномы
.
Вне интервала –1 Ф Ф W Ф 1 полиномы ![]() также
представляются в тригонометрической форме:
также
представляются в тригонометрической форме:
![]() . (2.16в)
. (2.16в)
Анализ поведения полиномов Чебышева
показывает, что в интервале –1 Ф W Ф 1 угол ![]() изменяется
от –p (при W = –1) до 0 (при W = 1), поэтому полином
изменяется
от –p (при W = –1) до 0 (при W = 1), поэтому полином ![]() ровно
m раз принимает значения, равные нулю, и m + 1 раз достигает значений,
равных +1 или –1 и чередующихся друг с другом. Вне интервала –1 Ф W Ф
1 полином
ровно
m раз принимает значения, равные нулю, и m + 1 раз достигает значений,
равных +1 или –1 и чередующихся друг с другом. Вне интервала –1 Ф W Ф
1 полином ![]() согласно
формуле (2.16в) монотонно возрастает. В качестве примера на рис. 2.6, а
изображен график полинома Чебышева
согласно
формуле (2.16в) монотонно возрастает. В качестве примера на рис. 2.6, а
изображен график полинома Чебышева ![]() ,
т. е. полинома четвертого порядка.
,
т. е. полинома четвертого порядка.
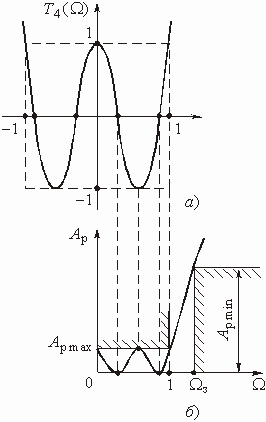
Рис. 2.6
В соответствии с (2.15) рабочее
ослабление ![]() фильтра
Чебышева на тех частотах W , где полином
фильтра
Чебышева на тех частотах W , где полином ![]() обращается
в нуль, также обращается в нуль. На частотах, на которых
обращается
в нуль, также обращается в нуль. На частотах, на которых ![]() равен
± 1, рабочее ослабление достигает величины
равен
± 1, рабочее ослабление достигает величины
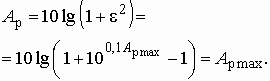
С ростом значений полинома ![]() на
частотах W > 1 рабочее ослабление
на
частотах W > 1 рабочее ослабление ![]() также
монотонно растет. На рис. 2.6, б приведен график рабочего ослабления
фильтра Чебышева четвертого порядка.
также
монотонно растет. На рис. 2.6, б приведен график рабочего ослабления
фильтра Чебышева четвертого порядка.
Фильтры Чебышева называют также фильтрами с равноволновой характеристикой ослабления в полосе пропускания.
На рис. 2.7 показаны частотные
зависимости квадрата АЧХ фильтра Чебышева для различных значений m, полученные
для ![]() из (2.15).
Подобные зависимости могут быть построены для рабочего ослабления фильтра.
из (2.15).
Подобные зависимости могут быть построены для рабочего ослабления фильтра.
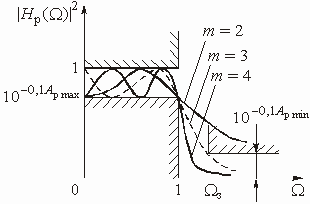
Рис. 2.7
Чтобы характеристики фильтра отвечали
требованиям в полосе непропускания, необходимо выбрать порядок фильтра m
из условия ![]() Ф
Ф
![]() . Для полосы
непропускания
. Для полосы
непропускания ![]() определяется
формулой (2.16в), следовательно,
определяется
формулой (2.16в), следовательно, ![]() Х
Х
![]() . Отсюда
. Отсюда ![]() Х
Х
![]() . Далее
. Далее ![]() Х
Х
![]() и
m Х
и
m Х 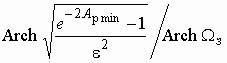 .
.
В этой формуле величина ![]() измеряется
в неперах. При использовании единицы децибел порядок фильтра вычисляется из
выражения
измеряется
в неперах. При использовании единицы децибел порядок фильтра вычисляется из
выражения
m Х
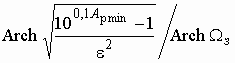 .
.
Сравнивая частотные характеристики
фильтров Баттерворта и Чебышева, следует указать, что полиномы Чебышева являются
полиномами наилучшего приближения. Это означает, что при одинаковом значении
m из всех полиномиальных фильтров, ослабления которых в полосе пропускания
не превышают ![]() ,
наибольшие значения ослабления в полосе непропускания имеет фильтр Чебышева.
В частности, рабочее ослабление фильтра Чебышева в полосе непропускания может
превышать (и весьма значительно) рабочее ослабление фильтра Баттерворта при
равных значениях m и
,
наибольшие значения ослабления в полосе непропускания имеет фильтр Чебышева.
В частности, рабочее ослабление фильтра Чебышева в полосе непропускания может
превышать (и весьма значительно) рабочее ослабление фильтра Баттерворта при
равных значениях m и ![]() .
Однако характеристика рабочего ослабления фильтра Баттерворта имеет в полосе
пропускания монотонный характер и легче поддается корректированию для устранения
искажений передаваемых сигналов.
.
Однако характеристика рабочего ослабления фильтра Баттерворта имеет в полосе
пропускания монотонный характер и легче поддается корректированию для устранения
искажений передаваемых сигналов.
Выбор типа полиномиальных фильтров определяется конкретными условиями их применения в аппаратуре связи и радиотехнических устройствах.
Для получения передаточной функции
фильтра Чебышева поступим аналогично тому, как делали это для фильтров Баттерворта.
Заменим оператор jW на оператор р и перейдем от функции ![]() к
функции
к
функции
![]() .
.
Представим полином ![]() в
виде (2.16б) и найдем полюсы функции
в
виде (2.16б) и найдем полюсы функции ![]() ,
решив уравнение
,
решив уравнение
![]() . (2.17)
. (2.17)
Поскольку согласно (2.16а) коэффициент
при старшем члене полинома Чебышева ![]() равен
равен
![]() , то коэффициент
при старшем члене полинома в левой части приведенного выше уравнения равен
, то коэффициент
при старшем члене полинома в левой части приведенного выше уравнения равен ![]() .
.
Корни уравнения (2.17), как можно доказать, определяются аналитически следующим выражением:
![]() , (2.18)
, (2.18)
где ![]() .
.
Из корней в левой полуплоскости
составляются сомножители ![]() ,
и по теореме Виета строится передаточная функция фильтра
,
и по теореме Виета строится передаточная функция фильтра
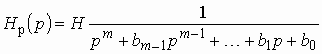 ,
,
где ![]() .
.
В заключение отметим, что для полиномиальных
фильтров в справочниках составлены весьма полные таблицы полюсов и коэффициентов
передаточных функций для различных величин ![]() и
m. Порядок же фильтров m определяется по специальным графикам,
исходя из заданных величин
и
m. Порядок же фильтров m определяется по специальным графикам,
исходя из заданных величин ![]() ,
,
![]() и
и ![]() .
.

Частотные характеристики полиномиальных фильтров, описываемые выражениями (2.1) – (2.3), имеют монотонный характер в полосе непропускания. В частности, рабочее ослабление таких фильтров монотонно возрастает по мере удаления от полосы пропускания (рис. 2.4, а и 2.6, б).
При “жестких” требованиях к частотным характеристикам (малая переходная область между полосами пропускания и непропускания и большая величина рабочего ослабления в полосе непропускания) порядок фильтра m может получиться очень большим даже в случае применения полинома Чебышева. Это приведет к существенному усложнению фильтра и к излишнему “расходу” элементов.
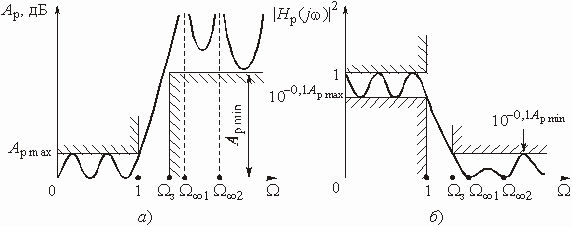
Рис. 2.8
В таких случаях целесообразно применять
фильтры со всплесками рабочего ослабления в полосе непропускания (рис.
2.8, а). На частотах всплеска ![]() ,
,
![]() и т. д. рабочее
ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна
характеристики ослабления в переходной области. Соответственно АЧХ фильтра на
частотах
и т. д. рабочее
ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна
характеристики ослабления в переходной области. Соответственно АЧХ фильтра на
частотах ![]() ,
,
![]() и т. д. будет
обращаться в нуль (рис. 2.8, б).
и т. д. будет
обращаться в нуль (рис. 2.8, б).
Для выполнения указанных условий в выражениях (2.2) – (2.3) используют рациональные дроби вида:
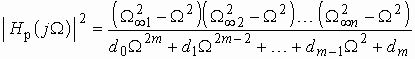 ; (2.19)
; (2.19)
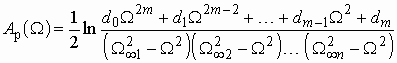 . (2.20)
. (2.20)
Действительно, когда W принимает
значения ![]()
![]() 0
и
0
и ![]() .
.
Передаточная функция таких фильтров является дробно-рациональной:
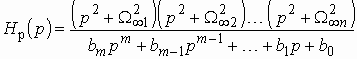 (2.21)
(2.21)
и кроме полюсов ![]() имеет
нули
имеет
нули
![]() .
.
Фильтры со всплесками рабочего ослабления называют еще фильтрами с нулями передачи.
Среди фильтров со всплесками ослабления
наиболее широкое распространение получили фильтры, построенные на основе дробей
Чебышева и Золотарева. Чтобы получить частотные характеристики фильтра на основе
дробей Чебышева, нужно в формулах (2.14) или (2.15) использовать в качестве
функции фильтрации дробь Чебышева. Обозначая ее ![]() ,
получим
,
получим
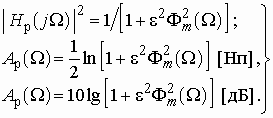 (2.22)
(2.22)
В качестве примера укажем дробь
Чебышева пятого порядка, для которой построены графики ![]() и
и
![]() на рис. 2.8,
а и б:
на рис. 2.8,
а и б:
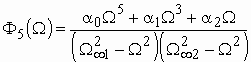 ,
,
где ![]() ,
,
![]() и
и ![]() –
коэффициенты, связанные с частотами всплеска
–
коэффициенты, связанные с частотами всплеска ![]() и
и
![]() .
.
Очевидно, что подстановка этой дроби в (2.22) приведет после некоторых преобразований к выражениям общего вида (2.19) и (2.20).
В полосе пропускания дробь Чебышева
ведет себя так же, как и полином Чебышева, т. е. рабочее ослабление фильтра
носит равноволновый характер. На частотах всплеска ![]() и
и
![]() дробь Чебышева
обращается в бесконечность, что приводит к бесконечно большому рабочему ослаблению.
дробь Чебышева
обращается в бесконечность, что приводит к бесконечно большому рабочему ослаблению.
Следует отметить, что дробь Чебышева
является дробью наилучшего приближения. Это означает, что фильтр на основе дроби
Чебышева на любой частоте полосы непропускания имеет большее значение рабочего
ослабления по сравнению с фильтрами на основе других дробей (и полиномов, как
частных случаев дробей) при прочих равных условиях (при одинаковых порядках
m, при таком же количестве и расположении частот всплеска и тех же величинах
![]() ).
).
Частным случаем дробей Чебышева являются дроби Золотарева:
![]() ,
(2.23)
,
(2.23)
где ![]() ,
,
![]() , значение
S равно 0 для четных m и равно 1 для нечетных m; m
– порядок дроби;
, значение
S равно 0 для четных m и равно 1 для нечетных m; m
– порядок дроби; ![]() ,
,
![]() – нули и полюсы
дроби, связанные соотношением
– нули и полюсы
дроби, связанные соотношением ![]() .
.
Используя в качестве функции фильтрации в (2.14) и (2.15) дроби Золотарева, получим
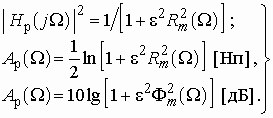 (2.24)
(2.24)
Из формул (2.23) и (2.24) следует,
что нули функции ![]() совпадают
с нулями дроби Золотарева, а всплески функции
совпадают
с нулями дроби Золотарева, а всплески функции ![]() –
с полюсами этой же дроби. Нули и полюсы дроби Золотарева можно рассчитывать,
однако обычно их определяют по каталогам для операторных передаточных функций
ФНЧ. На рис. 2.9 показан график
–
с полюсами этой же дроби. Нули и полюсы дроби Золотарева можно рассчитывать,
однако обычно их определяют по каталогам для операторных передаточных функций
ФНЧ. На рис. 2.9 показан график ![]() для
фильтра Золотарева пятого порядка.
для
фильтра Золотарева пятого порядка.
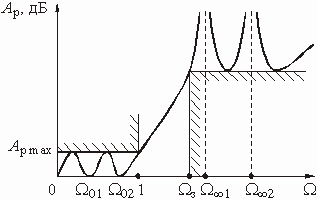
Рис. 2.9
Дроби Золотарева так же, как и
полиномы Чебышева, дают равноволновую характеристику рабочего ослабления фильтра
в полосе пропускания. Однако в полосе непропускания у фильтров Золотарева значения
всех минимумов рабочего ослабления оказываются одинаковыми и равными значению
рабочего ослабления на частоте ![]() .
Такие фильтры называются также фильтрами с изоэкстремальными характеристиками
рабочего ослабления.
.
Такие фильтры называются также фильтрами с изоэкстремальными характеристиками
рабочего ослабления.
Фильтры с характеристиками Золотарева можно рассматривать как частный случай фильтров с характеристиками Чебышева, когда значения минимумов ослабления фильтра в полосе непропускания выравнены, а число всплесков – максимально возможное при выбранном значении m.

Любые из рассмотренных выше фильтров, как полиномиальные, так и со всплесками ослабления, в зависимости от особенностей их применения могут быть реализованы либо в виде пассивных LC-цепей, либо в виде активных RC-цепей.
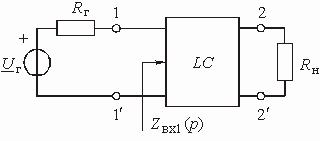
Рис. 2.10
Пассивные LC-фильтры обычно
представляют собой реактивный лестничный четырехполюсник, включенный между генератором
с активным внутренним сопротивление ![]() и
нагрузкой с активным сопротивлением
и
нагрузкой с активным сопротивлением ![]() (рис.
2.10). Входное сопротивление реактивного четырехполюсника, нагруженного на сопротивление
(рис.
2.10). Входное сопротивление реактивного четырехполюсника, нагруженного на сопротивление
![]() , обозначено
на рисунке
, обозначено
на рисунке ![]() .
.
Если фильтр со стороны зажимов
1 – 1ў рассматривать как двухполюсник, образованный реактивным четырехполюсником
и нагрузкой ![]() ,
то, зная выражение
,
то, зная выражение ![]() ,
можно реализовать данный двухполюсник одним из известных в теории цепей методов
синтеза двухполюсников. Таким образом, задача реализации фильтра сводится к
реализации двухполюсника по его заданному входному сопротивлению. Идея данного
подхода принадлежит С. Дарлингтону и метод реализации фильтров называется методом
Дарлингтона.
,
можно реализовать данный двухполюсник одним из известных в теории цепей методов
синтеза двухполюсников. Таким образом, задача реализации фильтра сводится к
реализации двухполюсника по его заданному входному сопротивлению. Идея данного
подхода принадлежит С. Дарлингтону и метод реализации фильтров называется методом
Дарлингтона.
На входе фильтра имеет место несогласованность, которую можно оценить, введя в рассмотрение коэффициент отражения
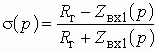 . (2.25)
. (2.25)
Решая (2.25) относительно ![]() ,
получаем
,
получаем
![]() . (2.26)
. (2.26)
В (2.26) неизвестным является коэффициент
отражения ![]() .
В свою очередь, коэффициент отражения
.
В свою очередь, коэффициент отражения ![]() связан
с передаточной функцией
связан
с передаточной функцией ![]() следующим
соотношением:
следующим
соотношением:
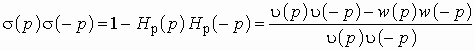 . (2.27)
. (2.27)
Из (2.27) следует, что знаменатель
у ![]() такой же,
как и у
такой же,
как и у ![]() : им
является полином
: им
является полином ![]() .
Остается найти нули правой части выражения (2.7) и половину из них “приписать”
полиному числителя
.
Остается найти нули правой части выражения (2.7) и половину из них “приписать”
полиному числителя ![]() .
Последний формируется из нулей по теореме Виета.
.
Последний формируется из нулей по теореме Виета.
Аналогично рассмотренному примеру решается задача реализации фильтра любого порядка. Например, полиномиальный ФНЧ пятого порядка (m = 5) реализуется в виде одной из двух схем, показанных на рис. 2.12, а и б. Количество реактивных элементов определяется порядком фильтра m. Отличие фильтра Баттерворта от фильтра Чебышева будет заключаться в этом случае только в разных значениях реактивных элементов, получаемых в процессе реализации соответствующих передаточных функций.
Рис. 2.12
По подобной схеме осуществляется
и реализация передаточных функций фильтров со всплесками затухания (Чебышева
или Золотарева). Разложение входного сопротивления таких фильтров в цепную дробь
приведет к схемам, содержащим резонансные контуры, в которых резонансы происходят
на частотах ![]() ,
... Наличие этих контуров и обеспечивает бесконечно большое затухание на частотах
всплеска.
,
... Наличие этих контуров и обеспечивает бесконечно большое затухание на частотах
всплеска.
Рис. 2.13
Так, ФНЧ пятого порядка со всплесками
затухания на частотах ![]() и
и
![]() реализуется
в виде одной из схем, приведенных на рис. 2.13, а и б. И в первой
и во второй схемах контуры рассчитаны на резонансные частоты
реализуется
в виде одной из схем, приведенных на рис. 2.13, а и б. И в первой
и во второй схемах контуры рассчитаны на резонансные частоты ![]() и
и
![]() . В первой
схеме в параллельных контурах происходят резонансы токов; сопротивления контуров
принимают бесконечно большие значения. В результате на частотах резонансов
. В первой
схеме в параллельных контурах происходят резонансы токов; сопротивления контуров
принимают бесконечно большие значения. В результате на частотах резонансов ![]() и
и
![]() наблюдается
“обрыв” продольных ветвей фильтра и сигнал от генератора в нагрузку не поступает,
т. е. фильтр вносит бесконечно большое ослабление. Во второй схеме в последовательных
контурах происходят резонансы напряжений; сопротивления контуров обращаются
в нуль. Таким образом, здесь на частотах
наблюдается
“обрыв” продольных ветвей фильтра и сигнал от генератора в нагрузку не поступает,
т. е. фильтр вносит бесконечно большое ослабление. Во второй схеме в последовательных
контурах происходят резонансы напряжений; сопротивления контуров обращаются
в нуль. Таким образом, здесь на частотах ![]() и
и
![]() поперечные
ветви “закорачивают” нагрузку и сигнал на выход фильтра не поступает. Таким
образом, имеет место бесконечно большое ослабление.
поперечные
ветви “закорачивают” нагрузку и сигнал на выход фильтра не поступает. Таким
образом, имеет место бесконечно большое ослабление.

Фильтры, представляющие собой комбинацию пассивной RC-цепи и активного элемента, называются активными RC-фильтрами. В качестве активного элемента чаще всего используются операционные усилители с двумя входами: инвертирующим и неинвертирующим.
Реализация передаточных функций
фильтров на активных RC-цепях осуществляется следующим образом. Заданную
функцию ![]() порядка
m разбивают на произведение передаточных функций не выше второго порядка,
т. е.
порядка
m разбивают на произведение передаточных функций не выше второго порядка,
т. е. ![]() .Каждую
передаточную функцию
.Каждую
передаточную функцию ![]() реализуют
в виде ARC-звена первого или второго порядка. Схему ARC-фильтра
получают путем каскадного соединения звеньев.
реализуют
в виде ARC-звена первого или второго порядка. Схему ARC-фильтра
получают путем каскадного соединения звеньев.
В практике проектирования активных RC--фильтров используется большое число схем, реализующих передаточные функции первого и второго порядка. Один из способов построения таких схем показан на рис. 2.14, а. Пассивная часть схемы представлена в виде цепи из элементов R и С. Между зажимами 2 и 3 включен операционный усилитель, в котором использован инвертирующий вход. Примером пассивной RC-цепи является схема, приведенная на рис. 2.14, б. Передаточная функция изображенной на рис. 2.14, б активной RC-цепи может быть получена любым из методов теории цепей и имеет вид:
Рис. 2.14
 . (2.28)
. (2.28)
Для реализации в виде такой цепи полиномиального фильтрового звена второго порядка с передаточной функцией
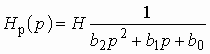 . (2.29)
. (2.29)
нужно выбрать проводимости ![]() ,
,
![]() и
и ![]() активными:
активными:
![]() ,
, ![]() и
и
![]() , а проводимости
, а проводимости
![]() и
и ![]() –
емкостными:
–
емкостными: ![]() и
и
![]() . Тогда (2.28)
запишется в следующей форме:
. Тогда (2.28)
запишется в следующей форме:
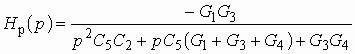 . (2.30)
. (2.30)
Сопоставление коэффициентов при р в соответствующих степенях и свободных членов из (2.30), выраженных через элементы фильтра, с заданными числовыми значениями коэффициентов при р и свободных членов из (2.29) позволяет определить значения элементов фильтра.
Реализация фильтров со всплесками ослабления, передаточные функции которых описываются выражением (2.21), осуществляется так же, как и реализация полиномиальных фильтров. Передаточная функция (2.21) разбивается на произведение простейших (первого и второго порядков) передаточных функций; последние реализуются в виде фильтровых RC-звеньев первого и второго порядков, соединяемых каскадно в общую схему фильтра.
Для реализации передаточных функций
второго порядка с нулем передачи ![]() используются
специальные фильтровые ARC-звенья.
используются
специальные фильтровые ARC-звенья.
Более подробно методику синтеза активных RC-фильтров со всплесками ослабления можно изучить, обратившись к специальной литературе.

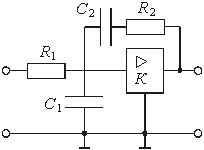
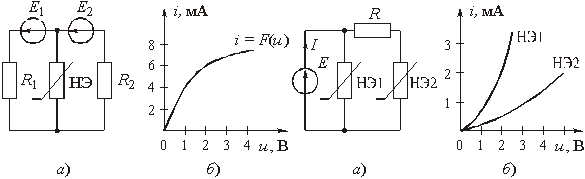
Для синтеза фильтров верхних частот (полосовых или заграждающих) и, в частности, для нахождения их передаточных функций, можно было бы заново повторить все преобразования, примененные к фильтрам нижних частот. Однако такой подход нерационален. Обычно для расчета ФВЧ, ПФ или ЗФ используют преобразование шкалы частот ФНЧ-прототипа.
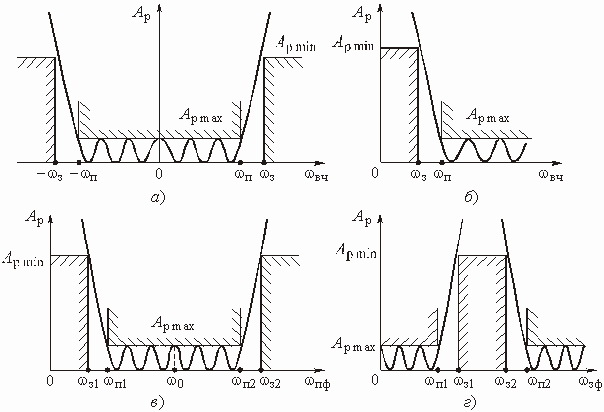
Рис. 2.16
На рис. 2.16 приведены характеристики ослабления фильтров: нижних частот (а), верхних частот (б) полосового (в) и заграждающего (г). Для ФНЧ эта характеристика построена как для положительных, так и для отрицательных частот. Шкала частот для каждого фильтра помечена для удобства буквенными обозначениями: “нч”, “вч”, “пф”, “зф”.
Из рис. 2.16, а и б видно, что характеристика ослабления ФНЧ в отрицательной области частот повторяет характеристику ФВЧ. Преобразовать характеристику ФНЧ в характеристику ФВЧ можно с помощью замены переменной
![]() , (2.31)
, (2.31)
где ![]() –
граничная частота полосы пропускания ФНЧ и ФВЧ. Действительно, такое преобразование
частоты приводит к соответствию: частоты
–
граничная частота полосы пропускания ФНЧ и ФВЧ. Действительно, такое преобразование
частоты приводит к соответствию: частоты ![]() частоте
частоте
![]() ; частоты
; частоты ![]() частоте
частоте
![]() ; частоты
; частоты ![]() частоте
частоте
![]() .
.
Чтобы из характеристики ФНЧ получить характеристику ПФ (рис. 2.16, в), необходима замена переменной
 , (2.32)
, (2.32)
где ![]() ;
;
![]() и
и ![]() –
граничные частоты полосы пропускания ПФ;
–
граничные частоты полосы пропускания ПФ; ![]() и
и
![]() – граничные
частоты полосы нерпопускания ПФ.
– граничные
частоты полосы нерпопускания ПФ.
Преобразование частоты (2.32)
приводит к соответствию частоты ![]() частоте
частоте
![]() , частоты
, частоты ![]() частоте
частоте
![]() , частоты
, частоты ![]() частоте
частоте
![]() .
.
Характеристику (рис. 2.16, г) заграждающего фильтра можно получить из характеристики ФНЧ, применяя преобразование частоты
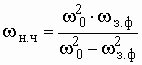 . (2.33)
. (2.33)

Замена переменных (2.31) и (2.32)
в выражении для квадрата АЧХ ![]() фильтра
нижних частот приводит при реализации этой функции к преобразованию схемы ФНЧ
в схемы ФВЧ и ПФ. Индуктивное сопротивление ФНЧ
фильтра
нижних частот приводит при реализации этой функции к преобразованию схемы ФНЧ
в схемы ФВЧ и ПФ. Индуктивное сопротивление ФНЧ ![]() переходит
при преобразовании частот (2.31) в сопротивление:
переходит
при преобразовании частот (2.31) в сопротивление:
![]() ,
,
т. е. в емкостное сопротивление
ФВЧ, где ![]() .
.
Емкостная проводимость
![]()
переходит в индуктивную проводимость
фильтра ВЧ с индуктивностью ![]() .
.
Преобразование частоты (2.32) приводит к замене индуктивного сопротивления ФНЧ
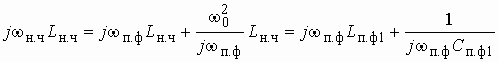
сопротивлением последовательного
контура в ПФ с элементами ![]() и
и
![]() .
.
Емкостная проводимость ФНЧ
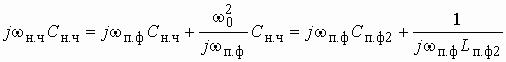
заменяется в ПФ проводимостью параллельного
контура с элементами ![]() и
и
![]() .
.
Нетрудно убедиться также, что индуктивный
элемент ФНЧ преобразуется в ЗФ в параллельный колебательный контур с резонансной
частотой ![]() ,
а емкость ФНЧ – в последовательный колебательный контур с той же резонансной
частотой.
,
а емкость ФНЧ – в последовательный колебательный контур с той же резонансной
частотой.
В активных RC-фильтрах для того, чтобы перейти от передаточной функции ФНЧ-прототипа к передаточным функциям ФВЧ и ПФ, следует осуществить замену комплексной переменной р. Из (2.31) получаем для ФВЧ
![]() или
или
![]() , (2.34)
, (2.34)
где ![]() и
и
![]() .
.
Заменяя в (2.34) оператор ![]() на
оператор р, запишем преобразование переменной р в выражении нормированной
по частоте передаточной функции ФНЧ-прототипа:
на
оператор р, запишем преобразование переменной р в выражении нормированной
по частоте передаточной функции ФНЧ-прототипа:
![]() . (2.35)
. (2.35)
Передаточная функция полиномиального звена второго порядка ФНЧ имеет вид:
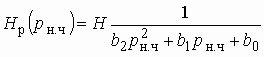 . (2.36)
. (2.36)
Замена переменной (2.35) в этом выражении приводит к передаточной функции полиномиального звена второго порядка ФВЧ
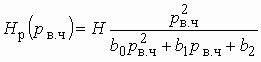 . (2.37)
. (2.37)
Для реализации звена с передаточной
функцией (2.37) может быть использована схема рис. 2.14, б, в которой
следует выбрать проводимости ![]() и
и
![]() – активными,
т. е.
– активными,
т. е. ![]() и
и ![]() ,
а проводимости
,
а проводимости ![]() ,
,
![]() и
и ![]() –
емкостными, т. е.
–
емкостными, т. е. ![]() ;
;
![]() и
и ![]() .
Подставляя эти значения проводимостей в выражение (2.28), получаем передаточную
функцию
.
Подставляя эти значения проводимостей в выражение (2.28), получаем передаточную
функцию
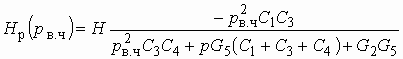 (2.38)
(2.38)
ARC-звена ФВЧ второго порядка, схема которого дана на рис. 2.18. Значения элементов схемы будут найдены, если приравнять коэффициенты из (2.37) и (2.38) при соответствующих степенях р.
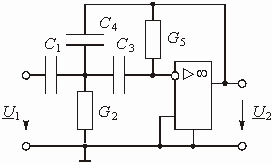
Рис. 2.18
Для перехода от НЧ-прототипа к полосовому фильтру воспользуемся (2.33):
![]() или
или
![]() , (2.39)
, (2.39)
где ![]() ;
;
![]() ;
; ![]() .
.
Вводя переменную ![]() и
учитывая, что
и
учитывая, что ![]() ,
находим из (2.39)
,
находим из (2.39)
![]() . (2.40)
. (2.40)
Такая замена переменной ![]() в
(2.36) приводит к передаточной функции полосового фильтра
в
(2.36) приводит к передаточной функции полосового фильтра
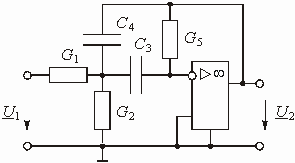
Рис. 2.19
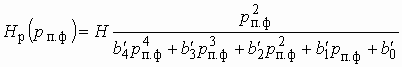 , (2.41)
, (2.41)
где ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Видим, что при переходе к ПФ порядок передаточной функции удваивается. Передаточную функцию (2.41) можно разбить на произведение передаточных функций второго порядка и каждую из них реализовать отдельной ARC-схемой.
Запишем передаточную функцию ПФ второго порядка:
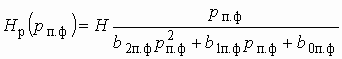 . (2.42)
. (2.42)
Подобную передаточную функцию имеет
ARC-схема, изображенная на рис. 2.14, б при ![]() ,
,
![]() ,
, ![]() ,
и
,
и ![]() ,
, ![]() .
Действительно, из (2.28) находим
.
Действительно, из (2.28) находим
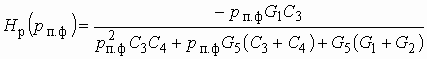 . (2.43)
. (2.43)
Элементы схемы фильтра (рис. 2.19) определяются сопоставлением (2.42) и (2.43).

В многоканальных системах передачи
разделение каналов по частоте осуществляется с помощью полосовых фильтров. Чтобы
сигналы одного канала не попадали в другой, ПФ должны иметь высокую избирательность.
Добротность резонансных контуров таких фильтров Q > 20 ... ![]() .
Так, для фильтра с
.
Так, для фильтра с ![]() =
62 кГц и полосой пропускания
=
62 кГц и полосой пропускания ![]() 4
кГц Q > 300, в то же время для фильтра с
4
кГц Q > 300, в то же время для фильтра с ![]() =
106 кГц и
=
106 кГц и ![]() 4
кГц Q > 1500.
4
кГц Q > 1500.
В радиосвязи используются еще более высокие частоты (десятки и сотни мегагерц) и для построения избирательных фильтров нужны резонаторы с добротностью в тысячи и десятки тысяч единиц. Такие значения добротности никогда не обеспечиваются в LC-резонаторах (их добротность не превышает сотен единиц), поэтому в фильтрах применяют высокодобротные механические резонаторы, пьезоэлектрические, магнитострикционные и электромеханические.
В пьезоэлектрических фильтрах роль резонатора выполняет пластинка, вырезанная специальным образом из материала, обладающего пьезоэлектрическим эффектом (например, из кристалла кварца). Пьезоэффект кварцевой пластинки заключается в появлении на ее поверхностях электрических зарядов при механическом воздействии на пластинку. Существует и обратный пьезоэффект – возникновение механических колебаний пьезопластинки при помещении ее в переменное электрическое поле.
Если пьезопластинку поместить между металлическими обкладками и подать на обкладки переменное напряжение, то пластинка начнет совершать механические колебания. На поверхностях пластинки возникнут электрические заряды и во внешней цепи потечет ток. При совпадении частоты переменного напряжения и частоты собственных колебаний пластинки возникает механический резонанс; амплитуда колебаний достигнет максимума и ток во внешней цепи будет максимальным. Таким образом, механический резонанс в кварцевой пластине подобен резонансу напряжений в последовательном колебательном контуре.
Эквивалентная схема пьезоэлектрического
(в частности, кварцевого) резонатора (рис. 2.20) помимо эквивалентных индуктивности
L и емкости C резонатора содержит емкость кварцедержателя ![]() ,
т. е. обкладок, между которыми помещена кварцевая пластинка.
,
т. е. обкладок, между которыми помещена кварцевая пластинка.
Пьезоэлектрические фильтры с кварцевыми резонаторами называют кварцевыми. Добротность кварцевых резонаторов достигает 10 ... 20 тыс. ед. Кварцевые фильтры могут быть построены по мостовой схеме (рис. 2.21).
Рис. 2.20 Рис. 2.21
Магнитострикционные фильтры строятся на основе резонаторов из ферромагнитного материала, обладающего магнитострикционным эффектом (например, из сплава никеля с кобальтом). Магнитострикционный эффект состоит в том, что стержень из ферромагнетика, помещенный в переменное магнитное поле, изменяет свои геометрические размеры. Обратный эффект – изменение магнитной проницаемости стержня при механическом воздействии на него. Если, например, никель-кобальтовый стержень поместить внутрь катушки индуктивности, создающей переменное магнитное поле, его геометрические размеры начнут меняться. При этом будет меняться и его магнитная проницаемость. В катушке индуктивности наведется ЭДС, направленная против ЭДС генератора и уменьшающая ток во внешней цепи. При механическом резонансе амплитуда колебаний стержня будет максимальной, а ток во внешней цепи – минимальный. Таким образом, механический резонанс магнитострикционного стержня подобен резонансу токов параллельного колебательного контура.
Эквивалентная схема резонатора
приведена на рис. 2.22 и включает в себя элементы ![]() и
и
![]() эквивалентного
резонатору контура, а также индуктивность
эквивалентного
резонатору контура, а также индуктивность ![]() ,
учитывающую рассеяние магнитного потока при замыкании его через воздух.
,
учитывающую рассеяние магнитного потока при замыкании его через воздух.
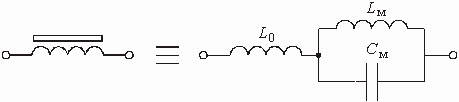
Рис. 2.22
Добротность магнитострикционных резонаторов ниже, чем кварцевых, и составляет 5 ... 10 тыс. ед. Магнитострикционные фильтры строятся по мостовой схеме (рис. 2.23).
Рис. 2.23 Рис. 2.24
В электромеханических фильтрах резонаторами являются металлические тела (диски, шарики, стержни, пластинки), соединенные металлическими связками. На рис. 2.24 изображен трехрезонаторный стержневой электромеханический фильтр. Возбуждаются колебания в фильтре с помощью входного магнитострикционного преобразователя (МСП); снимаются колебания с выхода фильтра с помощью выходного МСП. Электромеханические фильтры являются также высокодобротными.
Примеры к главе 2
Пример 2.1
Найти выражения для частотной характеристики
и передаточной функции фильтра нижних частот Баттерворта, удовлетворяющего следующим
требованиям: ![]() =
3 дБ;
=
3 дБ; ![]() = 12,2
дБ;
= 12,2
дБ; ![]() = 159 кГц;
= 159 кГц;
![]() = 318 кГц.
= 318 кГц.
Определим нормированную частоту
![]() = 2 и по формуле
(2.7) коэффициент неравномерности ослабления
= 2 и по формуле
(2.7) коэффициент неравномерности ослабления ![]() .
Порядок фильтра найдем согласно (2.11):
.
Порядок фильтра найдем согласно (2.11):
m Х
![]() .
.
Выберем m =2. Тогда в соответствии с (2.8) и (2.9)
![]() .
.
Найдем передаточную функцию фильтра
![]() . Значения
полюсов функции
. Значения
полюсов функции ![]() вычислим
из формулы (2.13):
вычислим
из формулы (2.13): ![]() =
0,707 + j0,707;
=
0,707 + j0,707; ![]() =
= – 0,707 + j0,707;
=
= – 0,707 + j0,707; ![]() =
– 0,707 – j0,707;
=
– 0,707 – j0,707; ![]() =
0,707 –
=
0,707 –
– j0,707. Расположение полюсов в комплексной плоскости показано
на рис. 2.5, а.
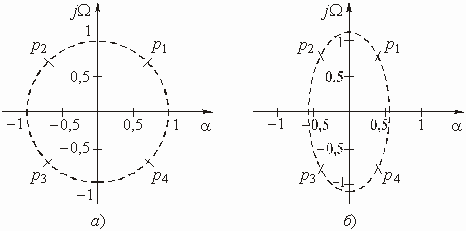
Рис. 2.5
По теореме Виета из полюсов в левой
полуплоскости ![]() и
и
![]() формируем передаточную
функцию
формируем передаточную
функцию
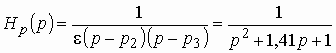 .
.
Пример 2.2
Построить передаточную функцию
фильтра Чебышева второго порядка (m = 2), рабочее ослабление в полосе
пропускания (от 0 до 159 кГц) которого не превышает величину ![]() =
3 дБ. Граничная частота полосы непропускания 318 кГц.
=
3 дБ. Граничная частота полосы непропускания 318 кГц.
Коэффициент неравномерности e
такого фильтра согласно (2.7) равен 1. Рабочее ослабление на частоте ![]() =
= 318/159 = 2 составляет
=
= 318/159 = 2 составляет ![]() 17
дБ, что почти на 5 дБ превышает рабочее ослабление на этой же частоте фильтра
Баттерворта второго порядка (см. Пример 2.1).
17
дБ, что почти на 5 дБ превышает рабочее ослабление на этой же частоте фильтра
Баттерворта второго порядка (см. Пример 2.1).
Расчет полюсов функции ![]() по
формулам (2.18) дает величины:
по
формулам (2.18) дает величины: ![]() =
0,322 + j0,777;
=
0,322 + j0,777; ![]() =
0,322 –
=
0,322 –
– j0,777; ![]() =
–0,322 – j0,777;
=
–0,322 – j0,777; ![]() =
–0,322 + j0,777. Расположение полюсов в комплексной плоскости показано
на рис. 2.5, б.
=
–0,322 + j0,777. Расположение полюсов в комплексной плоскости показано
на рис. 2.5, б.
Передаточная функция фильтра
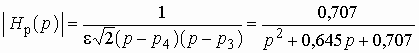 .
.
Пример 2.3
Реализовать фильтр нижних частот Баттерворта второго порядка из Примера 2.1 в виде пассивной LC-схемы. Внутреннее сопротивление генератора 1 кОм.
В Примере 2.1 была получена передаточная
функция Баттерворта второго порядка ![]() для
нормированных значений частоты
для
нормированных значений частоты ![]()
![]() ,
где
,
где ![]() . Реализация
нормированной передаточной функции приведет к схеме с нормированными значениями
реактивных элементов (обозначим их
. Реализация
нормированной передаточной функции приведет к схеме с нормированными значениями
реактивных элементов (обозначим их ![]() ),
которые затем необходимо денормировать для получения реальных значений.
),
которые затем необходимо денормировать для получения реальных значений.
В соответствии с (2.27)
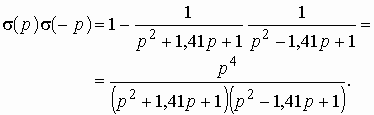
Нули этой функции ![]() .
Полином числителя
.
Полином числителя ![]() в
соответствии с теоремой Виета равен
в
соответствии с теоремой Виета равен ![]()
![]() .
Отсюда
.
Отсюда ![]() .
.
Согласно (2.26)
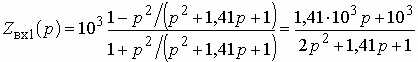 .
.
Реализацию двухполюсника со входным
сопротивлением ![]() осуществим
разложением в цепную (лестничную) дробь по методу Кауэра. Представим
осуществим
разложением в цепную (лестничную) дробь по методу Кауэра. Представим ![]() и
проведем разложение проводимости:
и
проведем разложение проводимости:
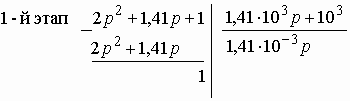
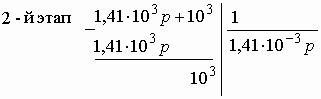
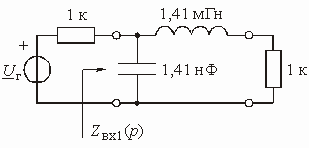
Рис. 2.11
Процесс разложения закончен. Входное
сопротивление ![]() ,
представленное цепной дробью, имеет вид
,
представленное цепной дробью, имеет вид
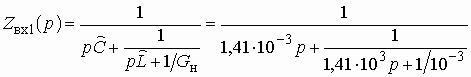 .
.
Схема двухполюсника, входное сопротивление
которого соответствует данной цепной (лестничной) дроби, приведена на рис. 2.11.
Нормированные значения элементов ![]() ,
,
![]() . Активная
проводимость нагрузки не нормируется и равна
. Активная
проводимость нагрузки не нормируется и равна ![]() См,
т. е. сопротивление нагрузки
См,
т. е. сопротивление нагрузки ![]() кОм.
Денормировать значения элементов можно следующим образом. Комплексная проводимость
нормированной емкости
кОм.
Денормировать значения элементов можно следующим образом. Комплексная проводимость
нормированной емкости ![]()
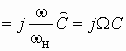 ,
откуда ненормированное значение емкости
,
откуда ненормированное значение емкости ![]() Ф
= 1,41 нФ.
Ф
= 1,41 нФ.
Подобным образом комплексное сопротивление
нормированной индуктивности 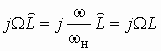 или
или
![]() Гн = 1,41
мГн.
Гн = 1,41
мГн.
Пример 2.4
Пусть задана передаточная функция полиномиального фильтра Чебышева пятого порядка.
![]() .
.
Полюсы этой функции (корни знаменателя):
![]() = –0,177;
= –0,177; ![]() ;
;
![]() . Вещественный
полюс
. Вещественный
полюс ![]() дает
по теореме Виета сомножитель первого порядка
дает
по теореме Виета сомножитель первого порядка ![]() ;
первая пара комплексно-сопряженных полюсов
;
первая пара комплексно-сопряженных полюсов ![]() и
и
![]() – сомножитель
второго порядка
– сомножитель
второго порядка ![]() ;
вторая пара полюсов
;
вторая пара полюсов ![]() и
и
![]() – сомножитель
– сомножитель
![]()
![]() .
Тогда
.
Тогда
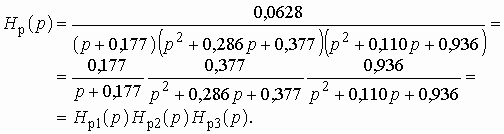
Таким образом, фильтр Чебышева пятого порядка может быть реализован двумя звеньями с передаточными функциями второго порядка и одним звеном с передаточной функцией первого порядка.
Пример 2.5
Реализовать фильтр нижних частот Баттерворта второго порядка из Примера 2.1 в виде активной RC-цепи.
Передаточная функция НЧ фильтра
Баттерворта второго порядка была получена ранее ![]() .
Для сопоставления с ней передаточной функции (2.30) представим последнюю в виде,
когда коэффициент при
.
Для сопоставления с ней передаточной функции (2.30) представим последнюю в виде,
когда коэффициент при ![]() равен
1:
равен
1:
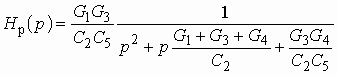 .
.
Приравнивая коэффициенты при р
и свободные члены этих передаточных функций, получаем три уравнения с шестью
неизвестными ![]() и
и
![]() :
: ![]() =
1;
=
1; ![]() ;
; ![]() .
.
Следует учесть, что в уравнения
входят нормированные значения емкостей ![]() и
и
![]() , так как коэффициенты
передаточной функции фильтра Баттерворта получены для нормированной частоты
, так как коэффициенты
передаточной функции фильтра Баттерворта получены для нормированной частоты
![]() (где
(где ![]()
![]() рад/с).
рад/с).
Поскольку искомых величин больше,
чем уравнений, зададимся частью из них. Выберем приемлемые значения проводимостей
![]() и
и ![]() ,
например
,
например ![]()
![]() См,
т. е.
См,
т. е. ![]() 1 кОм.
Далее из второго уравнения легко получить
1 кОм.
Далее из второго уравнения легко получить ![]()
![]() ,
а из первого и третьего уравнений –
,
а из первого и третьего уравнений – ![]()
![]() .
Денормированные значения емкостей
.
Денормированные значения емкостей ![]() нФ,
нФ,
![]() нФ.
нФ.
Схема фильтра приведена на рис. 2.15.
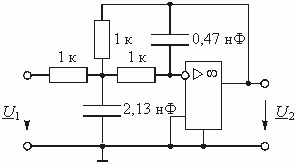
Рис. 2.15
Пример 2.6
Рассчитать полосовой фильтр с характеристиками
Баттерворта, удовлетворяющий требованиям: ![]() =
3 дБ;
=
3 дБ; ![]() = 12,2
дБ;
= 12,2
дБ; ![]() = 1241
кГц;
= 1241
кГц; ![]() = 1400
кГц;
= 1400
кГц; ![]() = 1168,5
кГц;
= 1168,5
кГц; ![]() = 1486
кГц.
= 1486
кГц.
Для решения поставленной задачи нужно сначала построить фильтр НЧ-прототипа, а затем с помощью преобразования частоты перейти к ПФ.
Пересчитаем требования ПФ (рис.
2.16, в) в требования к НЧ-прототипу (см. рис. 2.16, а). Воспользуемся
формулой (2.32): ![]() 1734,4
кГц;
1734,4
кГц; ![]() 159 кГц;
159 кГц;
![]()
![]() 318
кГц. В качестве нормирующей частоты выберем
318
кГц. В качестве нормирующей частоты выберем ![]() .
Тогда нормированные частоты
.
Тогда нормированные частоты ![]() и
и
![]() . Итак, требования
к НЧ-прототипу имеют вид:
. Итак, требования
к НЧ-прототипу имеют вид: ![]() =
3 дБ;
=
3 дБ; ![]() = 12,2
дБ;
= 12,2
дБ; ![]() = 159 кГц
(
= 159 кГц
(![]() );
); ![]() =
318 кГц (
=
318 кГц (![]() ).
).
В Примере 2.1 для такого НЧ-фильтра
были получены квадрат АЧХ ![]() ,
рабочее ослабление
,
рабочее ослабление ![]() и
передаточная функция
и
передаточная функция ![]()
![]() .
.
В Примере 2.3 это фильтр был реализован
в виде схемы, изображенной на рис. 2.11 с элементами ![]() = 1,41 мГн
и
= 1,41 мГн
и ![]() 1,41 нФ.
1,41 нФ.
При переходе к требуемому полосовому
фильтру необходимо индуктивность продольного плеча ![]() фильтра
НЧ-прототипа заменить последовательным контуром с элементами
фильтра
НЧ-прототипа заменить последовательным контуром с элементами ![]() = 1,41 мГн
и
= 1,41 мГн
и 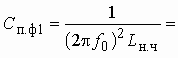
![]() Ф
= 6,0 пФ.
Ф
= 6,0 пФ.
Вместо емкости ![]() в
поперечном плече полосового фильтра будет включен параллельный контур с элементами
в
поперечном плече полосового фильтра будет включен параллельный контур с элементами
![]() 1,41 нФ
и
1,41 нФ
и 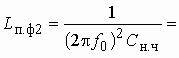
![]() Гн
= 6 мкГн.
Гн
= 6 мкГн.
Схема искомого полосового фильтра приведена на рис. 2.17.
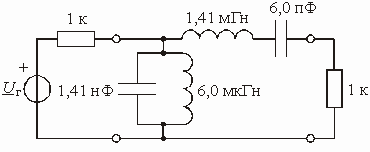
Рис. 2.17
Вопросы и задания для самопроверки
1. Что такое электрический фильтр? Какие типы фильтров существуют?
2. Характеристика рабочего ослабления фильтра изображена на рис. 2.3. Определить тип фильтра.
Ответ: ФНЧ Чебышева 5 порядка.
3. Какой вид имеют функции фильтрации фильтров Баттерворта, Чебышева, Золотарева?
4. Привести графики ![]() ФНЧ
третьего порядка Баттерворта, Чебышева и Золотарева.
ФНЧ
третьего порядка Баттерворта, Чебышева и Золотарева.
5. Рассчитать коэффициент
неравномерности ослабления в полосе пропускания и порядок фильтра Баттерворта,
удовлетворяющего требованиям: ![]() =
2 дБ;
=
2 дБ; ![]() =
25 дБ;
=
25 дБ; ![]() =
15 кГц;
=
15 кГц; ![]() =
26 кГц.
=
26 кГц.
Ответ: e = 0,765; m = 6.
6. Найти выражение для передаточной функции ФНЧ Баттерворта, удовлетворяющего требованиям, приведенным в задаче 5.
Ответ:
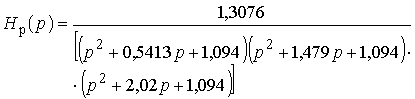 .
.
7. Рассчитать порядок и найти
операторную передаточную функцию ФНЧ Чебышева, удовлетворяющего требованиям:
![]() =
1,25 дБ;
=
1,25 дБ; ![]() =
30 дБ;
=
30 дБ; ![]() кГц;
кГц;
![]() кГц.
кГц.
Ответ: m =
3; 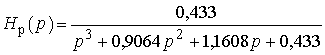 .
.
8. Привести LC-схемы фильтров, имеющих характеристики, изображенные на рис. 2.4.
9. Привести LC-схему фильтра, характеристика которого изображена на рис. 2.3.
10. Привести LC-схему фильтра НЧ Золотарева, а также график зависимости его рабочего ослабления от частоты.
11. Каков алгоритм расчета фильтров методом Дарлингтона?
12. Реализовать ФНЧ Баттерворта
третьего порядка, имеющего передаточную функцию 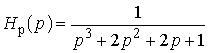 , в виде пассивной LC-схемы.
Внутреннее сопротивление генератора
, в виде пассивной LC-схемы.
Внутреннее сопротивление генератора ![]() .
.
Ответ: ![]() ,
, ![]() ,
, ![]() .
.
13. Какие фильтры называются активными -фильтрами?
14. Какие передаточные функции имеют -фильтровые звенья первого и второго порядков? Как получить передаточную функцию фильтра более высокого порядка?
15. Реализовать активный RC-фильтр, имеющий передаточную функцию, приведенную в задаче 12.
16. Как осуществить переход от ФНЧ к ФВЧ, ПФ, ЗФ?
17. Доказать, что при переходе от ФНЧ к ЗФ индуктивность фильтра-прототипа преобразуется в параллельный контур в ЗФ, а емкость – в последовательный контур?
18. Привести схемы LC-фильтров, имеющих характеристики, изображенные на рис. 2.16, б, в, г.
19. Рассчитать ФВЧ с максимально
плоской характеристикой ослабления, удовлетворяющий требованиям: ![]() =
1,5 дБ;
=
1,5 дБ; ![]() =
20 дБ;
=
20 дБ; ![]() ;
; ![]() .
.
20. Как осуществляется переход от схемы НЧ-прототипа к схемам ФВЧ и ПФ в активных RC-фильтрах?
21. Какие высокодобротные механические резонаторы используются для построения фильтров?
Глава 3. Амплитудные корректоры

Рассмотрим некоторую электрическую
цепь – четырехполюсник (рис. 3.1), имеющую амплитудно-частотную характеристику
(АЧХ), изображенную на рис. 3.2, а, а ослабление – на рис. 3.2, б.
Пусть для упрощения входной сигнал ![]() состоит из суммы всего двух гармоник с частотами
состоит из суммы всего двух гармоник с частотами ![]() и
2
и
2![]() (рис. 3.3,
а). Форма входного сигнала показана на этом рисунке жирной линией.
(рис. 3.3,
а). Форма входного сигнала показана на этом рисунке жирной линией.

Рис. 3.1
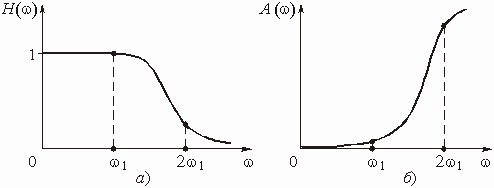
Рис. 3.2
Из анализа графиков АЧХ и ослабления цепи следует, что амплитуда первой гармоники при прохождении сигнала через цепь останется практически неизменной, а амплитуда второй гармоники уменьшится в несколько раз.
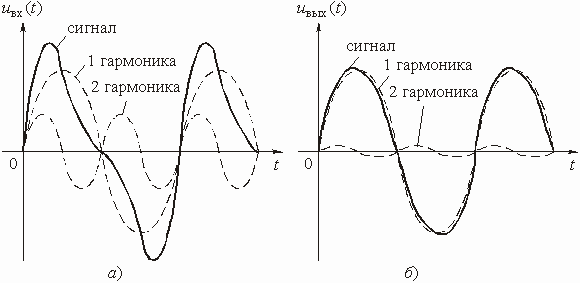
Рис. 3.3
Результат сложения гармоник на выходе цепи дает форму сигнала, отличающуюся от входной (рис. 3.3, б).
Изменение формы сигнала на выходе цепи по сравнению с формой сигнала на ее входе называется искажением сигнала. Когда искажения формы сигнала связаны с непостоянством амплитудно-частотной характеристики цепи, они носят название амплитудно-частотных искажений.
Таким образом, условием отсутствия амплитудно-частотных искажений в цепи следует считать постоянство ее АЧХ (ослабления) на всех частотах:
![]() ;
;
![]() . (3.1)
. (3.1)
На практике условие (3.1) часто не выполняется, т. е. АЧХ и ослабление цепей аппаратуры и линий связи не являются постоянными. Эти цепи практически всегда вносят амплитудно-частотные искажения в передаваемый сигнал. Устранить подобные искажения полностью не удается, но их можно уменьшить до величин, допустимых соответствующими нормами. Для этих цепей применяются амплитудные корректоры.
Амплитудный корректор – это четырехполюсник, который включается каскадно с цепью. Его задача заключается в том, чтобы дополнить АЧХ цепи или ее рабочее ослабление до постоянной величины на всех частотах рабочего диапазона. Вне рабочего диапазона АЧХ цепи может иметь любую форму.
На рис. 3.4 изображена цепь, работающая
между генератором с внутренним сопротивлением ![]() и
нагрузкой
и
нагрузкой ![]() .
Рабочий коэффициент передачи этой цепи в соответствии с (1.3) равен
.
Рабочий коэффициент передачи этой цепи в соответствии с (1.3) равен
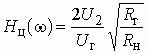 .
.
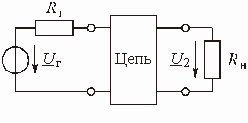
Рис. 3.4
Для достижения условий безискаженной
передачи между цепью и нагрузкой включен корректор (рис. 3.5). Чтобы режим работы
цепи не нарушался, входное сопротивление корректора должно равняться сопротивлению
нагрузки. Очевидно, только при этом условии напряжение на выходе цепи будет
равно ![]() , как
и в схеме рис. 3.4 до включения корректора.
, как
и в схеме рис. 3.4 до включения корректора.
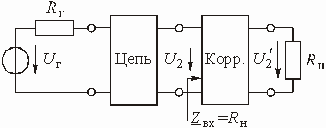
Рис. 3.5
Если обозначить напряжение на выходе
каскадного соединения цепи и корректора ![]() ,
то рабочий коэффициент передачи такого соединения запишется в виде
,
то рабочий коэффициент передачи такого соединения запишется в виде
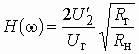 .
.
Разделим и умножим это выражение
на ![]() и представим
его в виде произведения двух сомножителей
и представим
его в виде произведения двух сомножителей
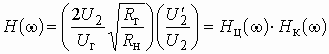 .
.
Первый сомножитель представляет рабочий коэффициент передачи цепи (см. рис. 3.4), а второй – коэффициент передачи по напряжению корректора.
Ослабление, вносимое каскадным соединением цепи и корректора,
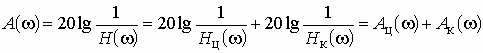
вычисляется путем сложения ослаблений цепи и корректора.
Из рис. 3.6 видно, что корректор
должен вносить ослабление, дополняющее ослабление цепи в рабочей полосе частот
![]() до постоянной
величины
до постоянной
величины ![]() .
.
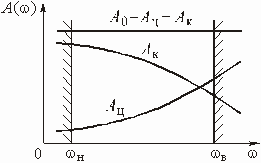
Рис. 3.6

Симметричный Т-перекрытый четырехполюсник
приведен на рис. 3.7. Сопротивления ![]() и
и
![]() выбираются
обратными, т. е.
выбираются
обратными, т. е. ![]() .
Если такой четырехполюсник нагрузить на сопротивление
.
Если такой четырехполюсник нагрузить на сопротивление ![]() ,
то его входное сопротивление окажется равным также
,
то его входное сопротивление окажется равным также ![]() .
.
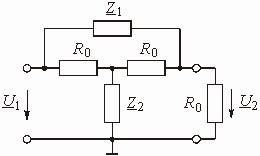
Рис. 3.7
Комплексная передаточная функция по напряжению схемы рис. 3.7 может быть вычислена по формуле
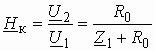 или
или
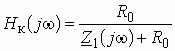 .
.
Операторная передаточная функция по напряжению имеет вид:
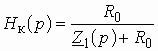 . (3.2)
. (3.2)
Вычислим ослабление, вносимое корректором:
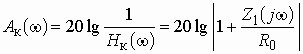 . (3.3)
. (3.3)
Данная формула показывает, что
зная поведение ![]() на
разных частотах, можно определить частотную зависимость ослабления
на
разных частотах, можно определить частотную зависимость ослабления ![]() .
.

Звенья 1-го порядка содержат по
одному реактивному элементу в двухполюсниках ![]() и
и
![]() . На рис.
3.10, а изображено такое звено с двухполюсником
. На рис.
3.10, а изображено такое звено с двухполюсником ![]() ,
состоящим из параллельного соединения элементов
,
состоящим из параллельного соединения элементов ![]() и
и
![]() .
.
Операторное сопротивление двухполюсника
![]() :
:
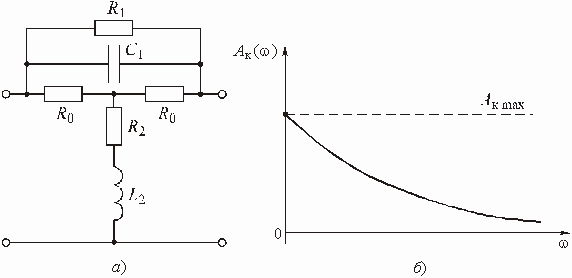
Рис. 3.10
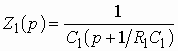 . (3.4)
. (3.4)
Если подставить выражение (3.4) в формулу (3.2), то получим операторную передаточную функцию звена:
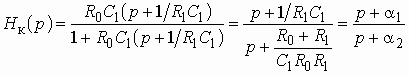 ,
,
где 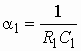 и
и
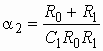 .
.
Частотная характеристика ослабления данного звена
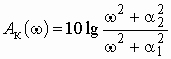 ; (3.5)
; (3.5)
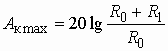
показана на рис. 3.10, б.
На рис. 3.11, а изображено
звено 1-го порядка с двухполюсником ![]() ,
состоящим из параллельного соединения
,
состоящим из параллельного соединения ![]() и
и
![]() . Операторная
передаточная функция этого звена
. Операторная
передаточная функция этого звена
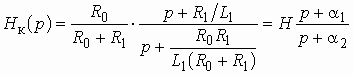 ,
,
где 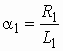 и
и
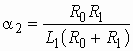 ,
, 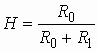 .
.
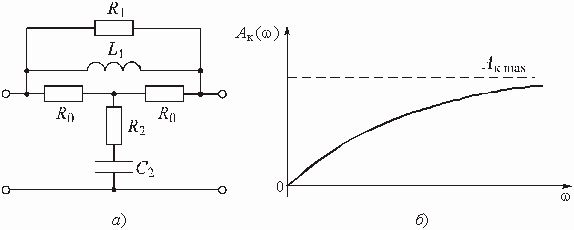
Рис. 3.11
Частотная характеристика ослабления звена
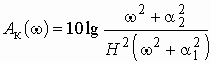
показана на рис. 3.11, б.
Максимальное значение ослабления корректора
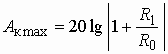 . (3.6)
. (3.6)
Звенья 2-го порядка содержат по
два реактивных элемента в двухполюсниках ![]() и
и
![]() . На рис.
3.12, а изображено звено, содержащее последовательный колебательный контур
и сопротивление
. На рис.
3.12, а изображено звено, содержащее последовательный колебательный контур
и сопротивление ![]() в
продольной ветви корректора. Операторная передаточная функция такого звена
в
продольной ветви корректора. Операторная передаточная функция такого звена
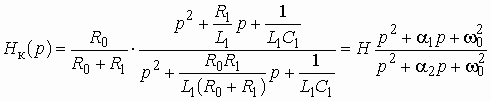 ,
,
где 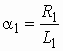 ,
,
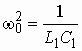 ,
, 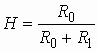 ,
,
![]() .
.
Частотная характеристика ослабления звена
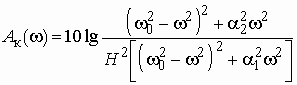
показана на рис. 3.12, б.
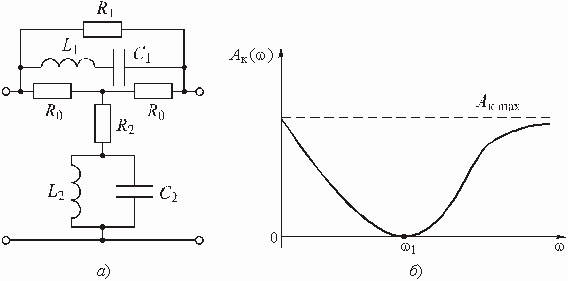
Рис. 3.12
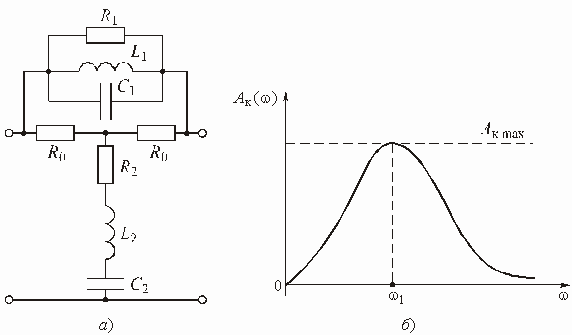
Рис. 3.13
Максимальное значение ![]() по-прежнему
рассчитывается по формуле (3.6).
по-прежнему
рассчитывается по формуле (3.6).
На рис. 3.13, а изображено
еще одно звено 2-го порядка с двухполюсником ![]() ,
представляющим собой параллельный колебательный контур. Операторная передаточная
функция звена и частотная характеристика ослабления (рис. 3.13, б) имеют
вид
,
представляющим собой параллельный колебательный контур. Операторная передаточная
функция звена и частотная характеристика ослабления (рис. 3.13, б) имеют
вид
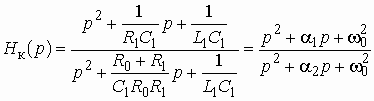 ,
,
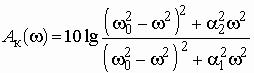 ,
,
где 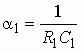 ,
,
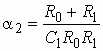 ,
, 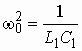 .
.
Значение ![]() на
графике рис. 3.12, б рассчитывается по формуле (3.6).
на
графике рис. 3.12, б рассчитывается по формуле (3.6).
Помимо Т-перекрытой схемы корректора (рис. 3.7) применяются также другие схемы, изображенные на рис. 3.15.
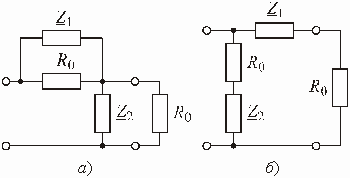
Рис. 3.15

Рис. 3.16
Передаточные функции, которые реализуются Т-перекрытым корректором, можно реализовать и элементарными четырехполюсниками, схемы которых приведены на рис. 3.16. Например, для четырехполюсника на рис. 3.16, а операторная передаточная функция
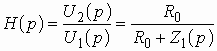
рассчитывается также, как и для корректора, построенного по Т-перекрытой схеме (см. формулу (3.2)). Цепи с элементарными четырехполюсниками применяются в случаях, когда не требуется согласование между генератором, корректором и нагрузкой.

Кроме пассивных схем амплитудных корректоров применяют активные схемы. Активные амплитудные корректоры строятся в общем случае с применением RC- и RLC-элементов, которые называют ARZ-цепями. Существует большое количество разновидностей активных звеньев эквивалентных по передаточной функции пассивным амплитудным корректорам. Две схемы таких активных звеньев изображены на рис. 3.17. Их передаточные функции выражаются соответствующими формулами (см. Примеры 1.5 и 1.4):
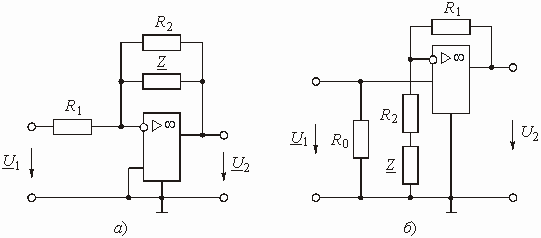
Рис. 3.17
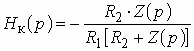 , (3.7)
, (3.7)
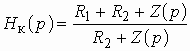 . (3.8)
. (3.8)
Если в схеме рис. 3.17, а в качестве двухполюсника Z выбрать последовательное соединение резистора R и емкости C, то передаточная функция (3.7) звена принимает вид
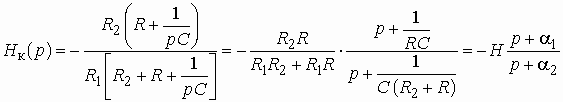 ,
,
где 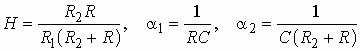 .
.
Частотная характеристика ослабления данного звена, также как и у пассивного звена 1-го порядка, вычисляется по формуле
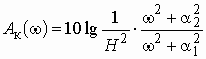 .
.
Данная функция при увеличении частоты
имеет монотонно возрастающий характер от величины 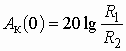 до
величины
до
величины ![]()
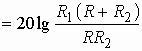 .
Если выбрать
.
Если выбрать ![]() и
и
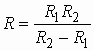 , то ослабление
будет изменяться от
, то ослабление
будет изменяться от ![]() до
нуля, оставаясь отрицательным (рис. 3.18, кривая 1).
до
нуля, оставаясь отрицательным (рис. 3.18, кривая 1).
Выберем в схеме 3.17, б в качестве двухполюсника Z емкость С. Тогда передаточная функция (3.8) этого звена принимает вид
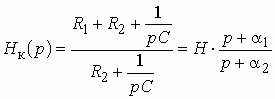 ,
,
где 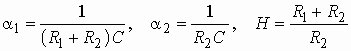 .
.
Частотная характеристика ослабления
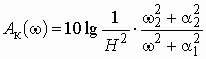 .
.
При увеличении частоты данная функция
имеет монотонно убывающий характер от ![]() до
до
![]() (рис. 3.18,
кривая 2).
(рис. 3.18,
кривая 2).
Если в качестве двухполюсника Z выбрать последовательный LC-контур, то частотная характеристика ослабления будет иметь вид, показанный на рис. 3.19, кривая 1. При выборе в качестве двухполюсника Z параллельного LC-контура частотная характеристика ослабления будет иметь обратный характер, как показано на рис. 3.19, кривая 2.
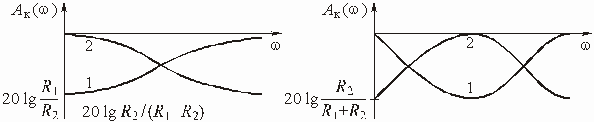
Рис. 3.18 Рис. 3.19
Несмотря на то, что рассмотренные схемы могут содержать индуктивности, они имеют ряд преимуществ по сравнению с пассивными амплитудными корректорами. Так, число реактивных элементов вдвое меньше, а ослабление, вносимое каскадным соединением цепи и корректора, близко к нулю. Последнее важно также потому, что дополнительное ослабление за счет применения пассивного корректора, как правило, приходится компенсировать с помощью усилителя, т. е. общая схема все равно оказывается активной.

При расчете пассивного амплитудного
корректора исходными данными являются: частотная характеристика ослабления цепи
![]() , подлежащая
коррекции в диапазоне частот
, подлежащая
коррекции в диапазоне частот ![]() ...
...
![]() ; точность
коррекции D A в этом же диапазоне частот; сопротивление нагрузки
; точность
коррекции D A в этом же диапазоне частот; сопротивление нагрузки ![]() .
.
Вначале определяют частотную характеристику
амплитудного корректора ![]() .
Для этого необходимо задать характеристику ослабления
.
Для этого необходимо задать характеристику ослабления ![]() каскадного
соединения цепи и корректора. Эта характеристика должна быть постоянной, не
зависящей от частоты, причем ее величину принимают несколько большей, чем максимальное
ослабление цепи:
каскадного
соединения цепи и корректора. Эта характеристика должна быть постоянной, не
зависящей от частоты, причем ее величину принимают несколько большей, чем максимальное
ослабление цепи:
![]() , (3.9)
, (3.9)
где ![]() =
1 ... 2 дБ.
=
1 ... 2 дБ.
Частотная характеристика ослабления амплитудного корректора вычисляется по формуле
![]() . (3.10)
. (3.10)
На рис. 3.6 в качестве примера
показаны характеристики ослабления цепи ![]() ,
ослабления
,
ослабления ![]() каскадного
соединения цепи и корректора, а также ослабления
каскадного
соединения цепи и корректора, а также ослабления ![]() корректора.
корректора.
Следующим этапом расчета амплитудного
корректора является выбор схемы корректора. Выбирают такую схему, которая в
диапазоне частот ![]() ...
...
![]() имеет нужный
характер частотной зависимости ослабления. Например, для реализации частотной
зависимости
имеет нужный
характер частотной зависимости ослабления. Например, для реализации частотной
зависимости ![]() ,
приведенной на рис. 3.6, можно использовать амплитудный корректор, в котором
двухполюсник
,
приведенной на рис. 3.6, можно использовать амплитудный корректор, в котором
двухполюсник ![]() состоит
из параллельного соединения емкости
состоит
из параллельного соединения емкости ![]() и
резистора
и
резистора ![]() (рис.
3.10).
(рис.
3.10).
Выбрав схему корректора, приступают
к ее расчету. При этом часто используется метод интерполирования. Согласно этому
методу задаемся числом точек интерполирования, равным числу элементов в двухполюснике
![]() . С учетом
формулы (3.3) составляется система уравнений вида
. С учетом
формулы (3.3) составляется система уравнений вида
где ![]() значения
параметров элементов двухполюсника
значения
параметров элементов двухполюсника ![]() .
Решение данной системы и дает значения
.
Решение данной системы и дает значения ![]() ,
которые являются параметрами индуктивностей, емкостей и резисторов.
,
которые являются параметрами индуктивностей, емкостей и резисторов.
Особенностями расчета является
то, что во-первых, параметры элементов могут быть отрицательными, а во-вторых
– точность коррекции может не удовлетворять заданным требованиям. Обычно приходится
данный расчет повторять. Если параметры элементов получились отрицательными,
то следует либо изменить величину ![]() в
формуле (3.9), либо положение точек интерполяции. Если параметры элементов получились
в конце концов положительными, то проверяется точность аппроксимации (коррекции).
Для этого по формуле (3.3) рассчитывается ослабление корректора
в
формуле (3.9), либо положение точек интерполяции. Если параметры элементов получились
в конце концов положительными, то проверяется точность аппроксимации (коррекции).
Для этого по формуле (3.3) рассчитывается ослабление корректора ![]() и
проверяется выполнение неравенства
и
проверяется выполнение неравенства
![]() Ф
D А.
Ф
D А.
При выполнении неравенства расчет
на этом заканчивается. В противном случае необходимо снова повторить расчет,
меняя точки интерполяции, до получения равноволновой характеристики погрешности.
Если при равноволновом характере погрешности требования к точности не выполняются,
то необходимо либо увеличить число элементов в двухполюснике, либо поделить
![]() пополам и
построить корректор в виде каскадного соединения двух четырехполюсников.
пополам и
построить корректор в виде каскадного соединения двух четырехполюсников.
Методика синтеза активных ARZ-корректоров
такая же, как и описанная выше методика расчета пассивных амплитудных корректоров.
Отличие заключается в том, что характеристика ослабления ![]() каскадного
соединения цепи и корректора выбирается близкой к нулю.
каскадного
соединения цепи и корректора выбирается близкой к нулю.
Используя каскадное соединение
различных типовых звеньев корректоров, можно получить частотные зависимости
ослабления ![]() любой
сложности. На рис. 3.22 изображена схема сложного корректора, построенного на
основе типовых схем (рис. 3.13), и его рабочее ослабление. Изменением характеристик
типовых схем добиваются получения требуемой характеристики амплитудного корректора.
любой
сложности. На рис. 3.22 изображена схема сложного корректора, построенного на
основе типовых схем (рис. 3.13), и его рабочее ослабление. Изменением характеристик
типовых схем добиваются получения требуемой характеристики амплитудного корректора.
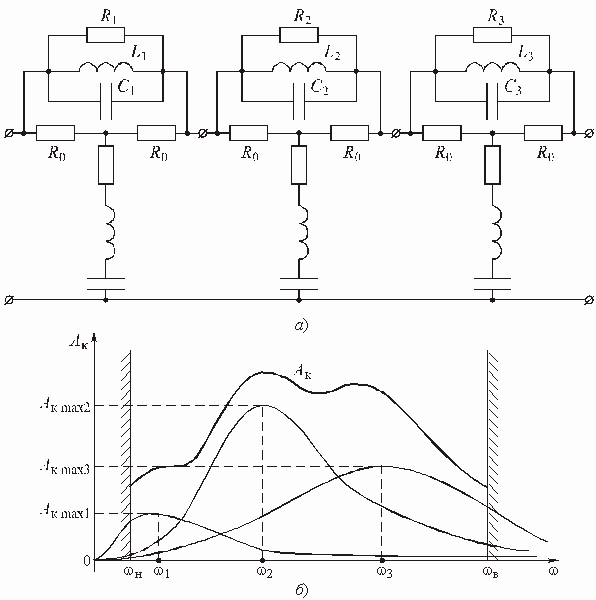
Рис. 3.22
Примеры к главе 3
Пример 3.1
Схема двухполюсника ![]() в
продольном плече корректора изображена на рис. 3.8, а. Построить график
частотной зависимости ослабления корректора
в
продольном плече корректора изображена на рис. 3.8, а. Построить график
частотной зависимости ослабления корректора ![]() .
.
Построим вначале график частотной
зависимости сопротивления реактивного двухполюсника ![]() ,
образованного элементами
,
образованного элементами ![]() ,
,
![]() ,
, ![]() и
и
![]() . На нулевой
частоте индуктивное сопротивление равно нулю, а емкостное – бесконечности, поэтому
. На нулевой
частоте индуктивное сопротивление равно нулю, а емкостное – бесконечности, поэтому
![]() . Двухполюсник
имеет три резонанса, причем первый – резонанс напряжений, на частоте
. Двухполюсник
имеет три резонанса, причем первый – резонанс напряжений, на частоте ![]() ,
второй – резонанс токов на частоте
,
второй – резонанс токов на частоте ![]() ,
третий – снова резонанс напряжений на частоте
,
третий – снова резонанс напряжений на частоте ![]() .
Это значит, что
.
Это значит, что ![]() ,
,
![]() . При
. При ![]() сопротивление
сопротивление
![]() также бесконечно
большое (рис. 3.8, б).
также бесконечно
большое (рис. 3.8, б).
Сопротивление ![]() ,
стоящее в продольном плече корректора, содержит помимо реактивных элементов
активное сопротивление
,
стоящее в продольном плече корректора, содержит помимо реактивных элементов
активное сопротивление ![]() (рис.
3.8, а). Поэтому на частотах, равных 0,
(рис.
3.8, а). Поэтому на частотах, равных 0, ![]() и
Ґ , на которых реактивное сопротивление
и
Ґ , на которых реактивное сопротивление ![]() стремится
к Ґ , полное сопротивление
стремится
к Ґ , полное сопротивление ![]() двухплюсника
ограничено величиной
двухплюсника
ограничено величиной ![]() (рис.
3.8, в).
(рис.
3.8, в).
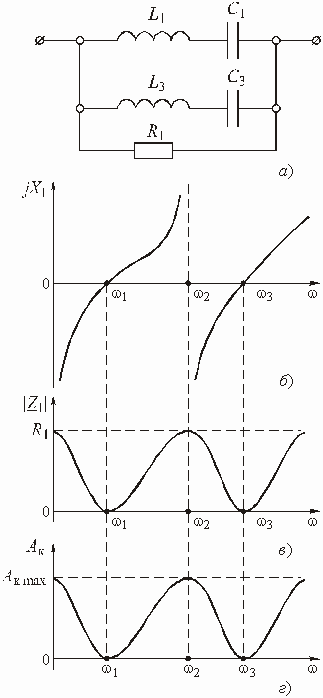
Рис. 3.8
Ослабление корректора ![]() рассчитывается
по формуле (3.3) и зависит от значений
рассчитывается
по формуле (3.3) и зависит от значений ![]() .
График
.
График ![]() повторяет
по форме график
повторяет
по форме график ![]() .
На частоте резонанса токов
.
На частоте резонанса токов ![]() ,
а также на частотах
,
а также на частотах ![]() и
и
![]() ослабление
корректора
ослабление
корректора ![]() достигает
своего максимального значения
достигает
своего максимального значения
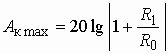 .
.
На частотах резонанса напряжений
![]() и
и ![]() значение
значение
![]() равно 0 (рис.
3.8, г).
равно 0 (рис.
3.8, г).
Пример 3.2
Задано ослабление ![]() цепи,
подлежащей коррекции (рис. 3.9, а). Привести схему корректора, выравнивающего
характеристику этой цепи до значения
цепи,
подлежащей коррекции (рис. 3.9, а). Привести схему корректора, выравнивающего
характеристику этой цепи до значения ![]() .
.
Находим требуемую характеристику
ослабления ![]() корректора
из условия
корректора
из условия ![]() =
=
![]() –
– ![]() .
График
.
График ![]() приведен
на этом же рис. 3.9, а.
приведен
на этом же рис. 3.9, а.
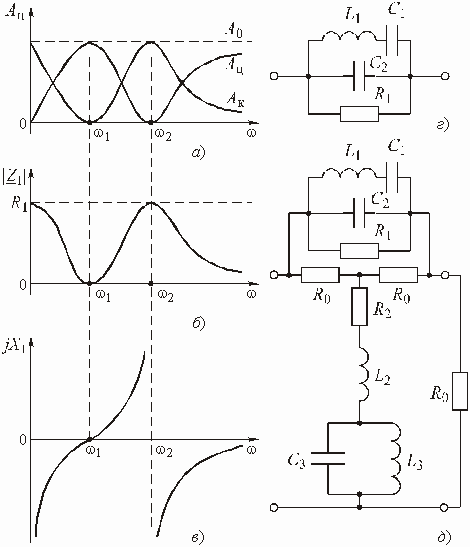
Рис. 3.9
По характеристике ![]() строим
графики частотной зависимости полного сопротивления
строим
графики частотной зависимости полного сопротивления ![]() и
реактивного сопротивления
и
реактивного сопротивления ![]() продольного
плеча корректора (рис. 3.9, б и 3.9, в).
продольного
плеча корректора (рис. 3.9, б и 3.9, в).
Из графиков рис. 3.9, в
и 3.9, б следует, что двухполюсник ![]() имеет
три реактивных элемента и одно активное сопротивление. В схеме два резонанса:
первым наступает резонанс напряжений на частоте
имеет
три реактивных элемента и одно активное сопротивление. В схеме два резонанса:
первым наступает резонанс напряжений на частоте ![]() ,
вторым – резонанс токов на частоте
,
вторым – резонанс токов на частоте ![]() .
Таким условиям удовлетворяет двухполюсник
.
Таким условиям удовлетворяет двухполюсник ![]() ,
изображенный на рис. 3.9, г. Двухполюсник
,
изображенный на рис. 3.9, г. Двухполюсник ![]() в
поперечном плече корректора является обратным двухполюснику
в
поперечном плече корректора является обратным двухполюснику ![]() .
.
Схема корректора приведена на рис. 3.9, д.
Пример 3.3
Определить элементы в поперечном
плече корректора (рис. 3.10, а), имеющего элементы ![]() =
600 Ом,
=
600 Ом, ![]() =
= 2400 Ом,
=
= 2400 Ом, ![]() =
60 нФ. Рассчитать и построить частотную зависимость ослабления корректора
=
60 нФ. Рассчитать и построить частотную зависимость ослабления корректора ![]() в
диапазоне частот 0 ё 8 кГц.
в
диапазоне частот 0 ё 8 кГц.
Элементы сопротивления ![]() в
поперечной ветви должны быть обратны сопротивлению
в
поперечной ветви должны быть обратны сопротивлению ![]() .
.
Из теории двухполюсников известно,
что для обратных двухполюсников ![]() .
Отсюда
.
Отсюда
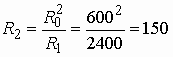 Ом,
Ом,
![]() мГн.
мГн.
Значения ![]() рассчитываем
по формуле (3.5) или по общей формуле (3.3), применимой для корректора любого
типа. Например, на частоте f = 0 получаем
рассчитываем
по формуле (3.5) или по общей формуле (3.3), применимой для корректора любого
типа. Например, на частоте f = 0 получаем
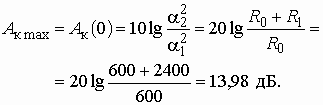
Остальные значения ![]() рассчитываются
аналогично. По результатам расчета простроен график
рассчитываются
аналогично. По результатам расчета простроен график ![]() ,
изображенный на рис. 3.14.
,
изображенный на рис. 3.14.
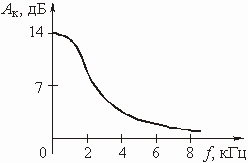
Рис. 3.14
Пример 3.4
Определить передаточную функцию
амплитудного корректора, построенного по схеме рис. 3.17, б, в которой
в качестве двухполюсника Z выбран последовательный колебательный
LC-контур. Рассчитать и построить частотную характеристику ослабления
![]() корректора
в диапазоне частот от 0 до
корректора
в диапазоне частот от 0 до ![]() =
100 кГц для элементов контура
=
100 кГц для элементов контура ![]() =
10 кОм,
=
10 кОм, ![]() = 20
кОм, L = 200 мГн, С = 1,268 нФ.
= 20
кОм, L = 200 мГн, С = 1,268 нФ.
Операционный усилитель в схеме
рис. 3.17, б включен по неинвертирующей схеме, поэтому передаточная функция
корректора определяется по формуле (3.8), в которой ![]() :
:
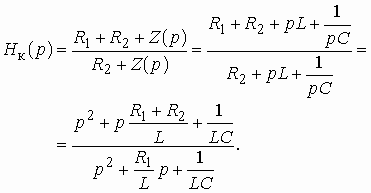
Частотная характеристика ослабления
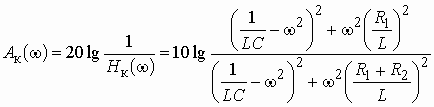 .
.
В формулах ![]() и
и
![]() величина
величина ![]() –
это квадрат резонансной частоты
–
это квадрат резонансной частоты ![]() LC-контура.
Для заданных значений L и С имеем
LC-контура.
Для заданных значений L и С имеем
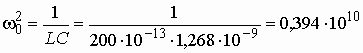 (рад/с)2.
(рад/с)2.
Резонансная частота ![]() =
10 кГц. Рассчитаем значения
=
10 кГц. Рассчитаем значения ![]() на
частотах, равных нулю,
на
частотах, равных нулю, ![]() =
10 кГц и
=
10 кГц и ![]() =
100 кГц.
=
100 кГц.
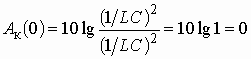 дБ,
дБ,
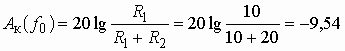 дБ,
дБ,
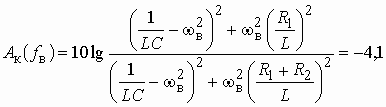 дБ.
дБ.
Аналогичным образом можно рассчитать
ослабление ![]() на
любой частоте в рабочем диапазоне. График
на
любой частоте в рабочем диапазоне. График ![]() изображен
на рис. 3.20.
изображен
на рис. 3.20.
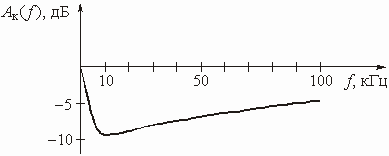
Рис. 3.20
Пример 3.5
В таблице 3.1 задана частотная
характеристика ослабления цепи ![]() .
Рассчитать элементы амплитудного корректора, если
.
Рассчитать элементы амплитудного корректора, если ![]() =
12 дБ и
=
12 дБ и ![]() =
200 Ом.
=
200 Ом.
Воспользуемся формулой (3.10) и
рассчитаем ослабление корректора ![]() в
диапазоне частот от 0 до 50 кГц.
в
диапазоне частот от 0 до 50 кГц.
Таблица 3.1
|
f, кГц |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
|
0,1 |
1,0 |
2,0 |
3,5 |
4,8 |
6,2 |
7,7 |
8,6 |
9,5 |
10,2 |
10,9 |
Результаты расчета ![]() приведены
в таблице 3.2, а на рисунке 3.21 изображены графики ослаблений
приведены
в таблице 3.2, а на рисунке 3.21 изображены графики ослаблений ![]() ,
,
![]() и
и ![]() .
.
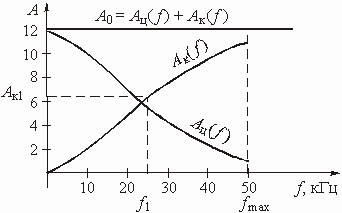
Рис. 3.21
Таблица 3.2
|
f, кГц |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
|
11,9 |
11,0 |
10,0 |
8,5 |
7,2 |
5,8 |
4,3 |
3,4 |
2,5 |
1,8 |
1,1 |
Частотная характеристика ослабления
![]() на рис. 3.21
может быть получена с помощью корректора, реализованного по схеме рис. 3.11,
в которой двухполюсник
на рис. 3.21
может быть получена с помощью корректора, реализованного по схеме рис. 3.11,
в которой двухполюсник ![]() состоит
из параллельного соединения элементов
состоит
из параллельного соединения элементов ![]() и
и
![]() .
.
Найдем ![]() из
формулы (3.6):
из
формулы (3.6):
![]() .
.
Значение ![]() =
10,9 дБ на частоте f = 50 кГц берем из таблицы 3.2. Получаем
=
10,9 дБ на частоте f = 50 кГц берем из таблицы 3.2. Получаем
![]() =
500 Ом.
=
500 Ом.
Для расчета ![]() выбираем
узел интерполяции:
выбираем
узел интерполяции: ![]() =
25 кГц,
=
25 кГц, ![]() =
6,2 дБ. Подставляем эти данные в формулу (3.3) или
=
6,2 дБ. Подставляем эти данные в формулу (3.3) или
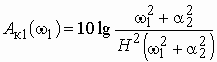 ,
,
где 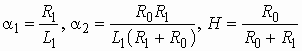 ,
,
![]() .
.
Получаем значение ![]() =
2 мГн.
=
2 мГн.
Значения параметров элементов ![]() и
и
![]() , образующих
обратный двухполюсник
, образующих
обратный двухполюсник ![]() ,
рассчитываем по формулам
,
рассчитываем по формулам
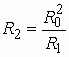 и
и
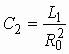 .
.
Получаем ![]() =
80 Ом и
=
80 Ом и ![]() =
0,05 мкФ. Расчетная характеристика ослабления корректора, вычисляемая по формуле
(3.3), точно совпадает с требуемой только на частотах
=
0,05 мкФ. Расчетная характеристика ослабления корректора, вычисляемая по формуле
(3.3), точно совпадает с требуемой только на частотах ![]() =
25 кГц и
=
25 кГц и ![]() =
50 кГц.
=
50 кГц.
Вопросы и задания для самопроверки
1. Почему происходят искажения сигнала на выходе цепи?
2. Сформулировать условие отсутствия амплитудно-частотных искажений в цепи.
3. Каким образом корректируются частотные характеристики цепей?
4. По какой схеме можно построить пассивный амплитудный корректор?
5. Как рассчитывается передаточная функция Т-перекрытого корректора и вносимое им ослабление?
6. Схема двухполюсника ![]() в
корректоре приведена на рис. 3.8, а.
Получить схему двухполюсника
в
корректоре приведена на рис. 3.8, а.
Получить схему двухполюсника ![]() . Построить
график частотной зависимости ослабления
. Построить
график частотной зависимости ослабления ![]() корректора.
корректора.
7. Какие схемы типовых звеньев пассивных корректоров известны? Какой вид имеют частотные характеристики вносимого ими ослабления?
8. Доказать, что частотная
характеристика ослабления ![]() звена,
изображенного на рис. 3.10, имеет вид (3.5), а максимальное значение ослабления
рассчитывается по формуле
звена,
изображенного на рис. 3.10, имеет вид (3.5), а максимальное значение ослабления
рассчитывается по формуле ![]() .
.
9. Доказать, что операторная передаточная функция элементарного четырехполюсника, изображенного на рис. 3.16, б, соответствует передаточной функции корректора (формула (3.2)).
10. Какие амплитудные корректоры называются активными?
11. Получить передаточную
функцию и частотную характеристику ослабления активного звена корректора,
изображенного на рис. 3.17, б, в
котором в качестве двухполюсника Z выбран параллельный
LC-контур. Подтвердить, что график рабочего ослабления ![]() такого
корректора – это кривая 2 на рис. 3.19.
такого
корректора – это кривая 2 на рис. 3.19.
Ответ:
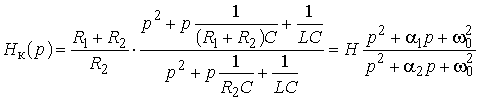 .
.
12. Каков порядок расчета пассивного амплитудного корректора?
13. Рассчитать элементы,
образующие двухполюсник ![]() амплитудного
корректора, частотная зависимость ослабления
амплитудного
корректора, частотная зависимость ослабления ![]() которого
приведена в таблице 3.3, а значение
которого
приведена в таблице 3.3, а значение ![]() =
200 Ом.
=
200 Ом.
Таблица 3.3
|
f, кГц |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
|
15,6 |
10,5 |
6,3 |
4,0 |
2,7 |
1,9 |
1,4 |
1,1 |
0,9 |
0,7 |
0,6 |
Ответ:
![]() =
1 кОм,
=
1 кОм, ![]() =
51 нФ.
=
51 нФ.
14. Зачем применяют каскадное соединение типовых звеньев корректоров?
Глава 4. Фазовые корректоры

Рассмотрим электрическую цепь –
четырехполюсник (рис. 4.1), имеющую фазо-частотную характеристику (ФЧХ) ![]() ,
изображенную на рис. 4.2, а, и характеристику группового времени прохождения
(ГВП)
,
изображенную на рис. 4.2, а, и характеристику группового времени прохождения
(ГВП) ![]() , являющуюся
производной от рабочей фазовой постоянной, – на рис. 4.2, б. Входной
сигнал
, являющуюся
производной от рабочей фазовой постоянной, – на рис. 4.2, б. Входной
сигнал ![]() состоит
из суммы двух гармоник с частотами
состоит
из суммы двух гармоник с частотами ![]() и
2
и
2![]() (рис. 4.3,
а). Форма входного сигнала изображена на этом рисунке жирной линией.
(рис. 4.3,
а). Форма входного сигнала изображена на этом рисунке жирной линией.
Анализ графиков ФЧХ и ГВП цепи показывает, что фаза первой гармоники почти не меняется при прохождении сигнала через цепь, а фаза второй гармоники существенно увеличивается.
В результате сложения гармоник на выходе цепи получается сигнал, форма которого отличается от входной (рис. 4.3, б).
Искажения формы сигнала при прохождении его по цепи, обусловленные нелинейностью фазо-частотной характеристики цепи или непостоянством группового времени прохождения, называются фазо-частотными искажениями.

Рис. 4.1
Условием отсутствия фазо-частотных
искажений в цепи следует считать линейность рабочей фазовой постоянной ![]() и
ФЧХ цепи (рис. 4.4, а)
и
ФЧХ цепи (рис. 4.4, а)
![]() (4.1)
(4.1)
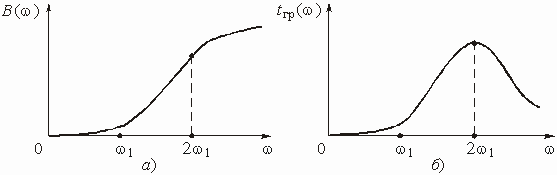
Рис. 4.2
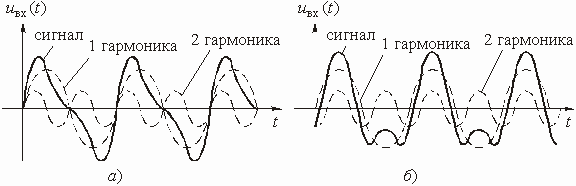
Рис. 4.3
Производная от фазо-частотной характеристики – это групповое время прохождения, которое для неискажающей цепи
![]() (4.2)
(4.2)
должна быть постоянной на всех частотах (рис. 4.4, б).
В реальных цепях условия (4.1) и (4.2) обычно не выполняются, т. е. ФЧХ не является линейной, а ГВП – не постоянно. Такие цепи вносят фазо-частотные искажения в передаваемый сигнал. Для уменьшения подобных искажений до допустимых значений применяют фазовые корректоры.
Фазовый корректор – это четырехполюсник, включаемый каскадно с цепью и дополняющий фазовую характеристику цепи до линейной. Вместо корректирования частотной характеристики фазы можно выравнивать характеристику группового времени прохождения так, чтобы она была постоянной на всех частотах рабочего диапазона. Фазовый корректор не должен искажать АЧХ цепи.
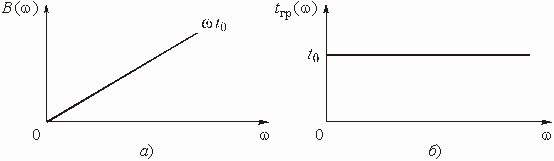
Рис. 4.4
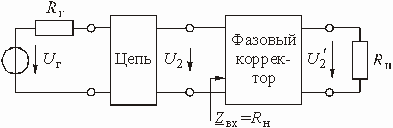
Рис. 4.5
На рис. 4.5 для достижения условий безискаженной передачи между генератором и нагрузкой включено каскадное соединение цепи с ФЧХ, подлежащей коррекции, и корректора. Входное сопротивление фазового корректора должно равняться сопротивлению нагрузки, чтобы условия работы цепи не изменялись по сравнению с теми, в которых находится цепь, включенная между генератором и нагрузкой в отсутствие корректора.
Передаточная функция цепи, изображенной на рис. 4.5,
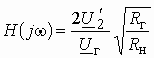 .
.
Умножим и разделим это выражение
на ![]() и представим
его в виде произведения передаточных функций цепи
и представим
его в виде произведения передаточных функций цепи ![]() и
корректора
и
корректора ![]()
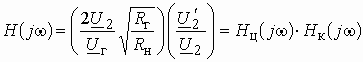 .
.
Фазо-частотная характеристика каскадного соединения цепи и корректора
![]() (4.3)
(4.3)
вычисляется как сумма ФЧХ цепи и корректора.
Из рис. 4.6 видно, что фазовый
корректор должен дополнять ФЧХ цепи в рабочей полосе частот ![]() до
линейной зависимости (рис. 4.6, а) либо дополнять групповое время
прохождения цепи до постоянной величины
до
линейной зависимости (рис. 4.6, а) либо дополнять групповое время
прохождения цепи до постоянной величины ![]() в
том же рабочем диапазоне частот (рис. 4.6, б). За пределами рабочего
диапазона ФЧХ и ГВП могут иметь любую форму.
в
том же рабочем диапазоне частот (рис. 4.6, б). За пределами рабочего
диапазона ФЧХ и ГВП могут иметь любую форму.
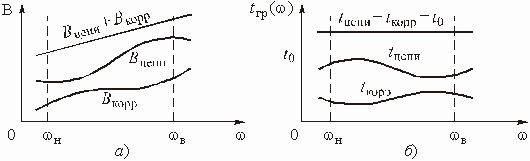
Рис. 4.6

Фазовые корректоры должны иметь
постоянное входное сопротивление и постоянное ослабление, которые не зависят
от частоты. Таким условиям удовлетворяют симметричные мостовые четырехполюсники
(рис. 4.7), у которых сопротивления ![]() и
и
![]() реактивные
и взаимообратные, т. е.
реактивные
и взаимообратные, т. е.
![]() и
и
![]() ,
, ![]() .
.
Такие четырехполюсники имеют с обеих сторон одинаковые характеристические сопротивления
![]() ,
,
поэтому его легко согласовывать с внутренним сопротивлением генератора и сопротивлением нагрузки.
Рабочее ослабление мостового симметричного
согласованно включенного четырехполюсника с взаимно-обратными сопротивлениями
![]() и
и ![]() равно
нулю на всех частотах:
равно
нулю на всех частотах: ![]() ,
т. е. эта схема не вносит никакого дополнительного ослабления сигнала.
,
т. е. эта схема не вносит никакого дополнительного ослабления сигнала.
Операторная передаточная функция по напряжению схемы рис. 4.7 имеет вид
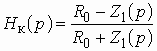 (4.4)
(4.4)
Комплексная передаточная функция
по напряжению схемы рис. 4.7, в которой ![]() и
и
![]() – реактивные
двухполюсники, может быть вычислена по формуле
– реактивные
двухполюсники, может быть вычислена по формуле
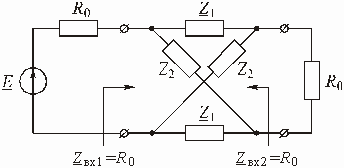
Рис. 4.7
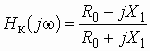 (4.5)
(4.5)
Нетрудно видеть, что модуль передаточной функции (4.5) равен 1,а аргумент и ГВП вычисляются по формулам:
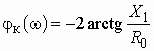 , (4.6)
, (4.6)
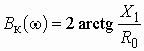 , (4.7)
, (4.7)
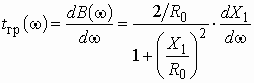 . (4.8)
. (4.8)
Формулы (4.6), (4.7) и (4.8) показывают,
что фазо-частотная характеристика, фазовая постоянная и характеристика группового
времени запаздывания корректора зависят только от вида двухполюсника ![]() .
.
На практике используются типовые звенья пассивных фазовых корректоров первого и второго порядков.
На рис. 4.8, а изображена
схема фазового корректора 1-го порядка, в котором двухполюсником ![]() является
индуктивность
является
индуктивность ![]() ,
а двухполюсником
,
а двухполюсником ![]() –
емкость
–
емкость ![]() .
.
Операторная передаточная функция этого корректора в соответствии с (4.4) имеет вид
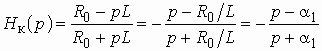 , (4.9)
, (4.9)
где ![]() .
.
Рабочая фазовая постоянная ![]() и
ГВП в соответствии с формулами (4.7) и (4.8)
и
ГВП в соответствии с формулами (4.7) и (4.8)
![]() , (4.10)
, (4.10)
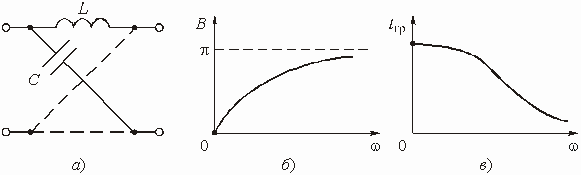
Рис. 4.8
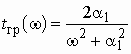 . (4.11)
. (4.11)
Графическое изображение данных характеристик показано на рис. 4.8, б и 4.8, в.
На рис. 4.9, а изображена
схема фазового корректора 2-го порядка, с двухполюсником ![]() ,
состоящим из последовательного соединения элементов
,
состоящим из последовательного соединения элементов ![]() и
и
![]() , т. е.
, т. е. 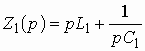 .
.
Операторная передаточная функция такого корректора в соответствии с (4.4) имеет вид
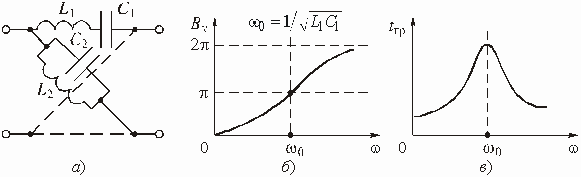
Рис. 4.9
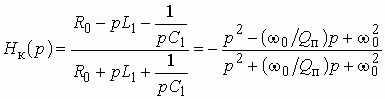 ,
,
где  ,
,
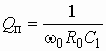 –добротность
полюса передаточной функции.
–добротность
полюса передаточной функции.
Комплексная передаточная функция
корректора получается при ![]()
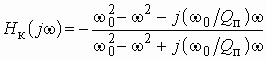 . (4.12)
. (4.12)
Модуль функции равен 1, а рабочая
фазовая постоянная ![]() и
ГВП
и
ГВП ![]() вычисляются
в соответствии с (4.7) и (4.8) по формулам
вычисляются
в соответствии с (4.7) и (4.8) по формулам
![]() ; (4.13)
; (4.13)
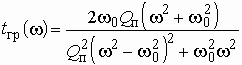 . (4.14)
. (4.14)
Графики зависимостей ![]() и
и
![]() фазового корректора
2-го порядка приведены на рис. 4.9, б и 4.9, в.
фазового корректора
2-го порядка приведены на рис. 4.9, б и 4.9, в.
Если известны коэффициенты передаточной
функции ![]() ,
,
![]() и нагрузка
и нагрузка
![]() , то параметры
элементов корректора рассчитываются по формулам
, то параметры
элементов корректора рассчитываются по формулам
![]() ; (4.15)
; (4.15)
![]() . (4.16)
. (4.16)
Рис. 4.12
Мостовая схема не всегда удобна в реализации, так как является уравновешенной. Существует ряд эквивалентных схем в виде неуравновешенной схемы, как показано на рис. 4.12. Заметим, что на практике добротность полюса больше единицы и поэтому чаще используется схема рис. 4.12, а, что удобно, так как она не содержит связанных индуктивностей с заданным коэффициентом связи. Неуравновешенные схемы по сравнению с мостовыми содержат вдвое меньше элементов.

Помимо пассивных фазовых корректоров применяют активные фазовые корректоры. Кроме пассивных RC или RLC-элементов схемы активных корректоров содержат операционные усилители. Существуют активные фазовые звенья 1-го и 2-го порядков. На рис. 4.13 приведена схема фильтрового звена на операционном усилителе. Передаточная функция этого звена вычисляется по формуле
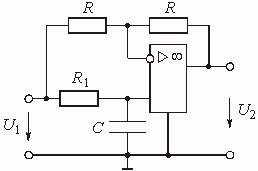
Рис. 4.13
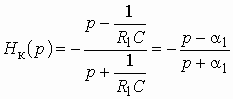 ,
(4.20)
,
(4.20)
где 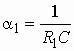 .
.
Выражение (4.20) аналогично формуле для расчета передаточной функции пассивного фазового корректора (4.9), т. е. схема, приведенная на рис. 4.13, – это активный корректор 1-го порядка.
Фазовые характеристики ![]() и
ГВП данного звена, также как у пассивного корректора 1-го порядка, вычисляются
по формулам
и
ГВП данного звена, также как у пассивного корректора 1-го порядка, вычисляются
по формулам
![]() ,
,
 .
.
График ![]() монотонно
нарастает от
монотонно
нарастает от ![]() до
до
![]() , а график
, а график
![]() монотонно
убывает от
монотонно
убывает от ![]() до
до
![]() . На рис. 4.14
показаны графики
. На рис. 4.14
показаны графики ![]() и
и
![]() , построенные
для разных значений
, построенные
для разных значений ![]() активного
корректора 1-го порядка.
активного
корректора 1-го порядка.
Рис. 4.14
На рис. 4.15 приведена еще одна
схема активного фазового корректора, также построенная на основе активного фильтрового
звена. Если в схеме рис. 4.15 задать ![]() ,
,
![]() , n
> 1, то передаточная функция, рассчитанная, например, с помощью метода узловых
напряжений, будет иметь вид
, n
> 1, то передаточная функция, рассчитанная, например, с помощью метода узловых
напряжений, будет иметь вид
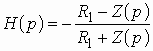 . (4.21)
. (4.21)
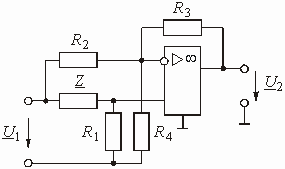
Рис. 4.15
Это передаточная функция фазового корректора (сравни с формулой (4.4)).
Если в качестве двухполюсника Z выбрать емкость, то передаточная функция (4.21) принимает вид (4.20):
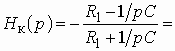
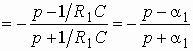 ,
,
т. е. схема на рис. 4.15 – это схема фазового корректора 1-го порядка.
Когда в качестве двухполюсника Z используется последовательный LC-контур, то получается передаточная функция фазового корректора 2-го порядка:
 ,
,
где ![]() ,
,
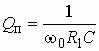 – добротность
полюса передаточной функции.
– добротность
полюса передаточной функции.
Графики частотных зависимостей
![]() и
и ![]() данного
корректора, полученные для разных значений
данного
корректора, полученные для разных значений ![]() ,
приведены на рис. 4.16.
,
приведены на рис. 4.16.
Рис. 4.16
Хотя активные ARZ-фазовые корректоры имеют индуктивность, но преимуществом их по сравнению с пассивными корректорами является меньшее количество элементов при том же порядке передаточных функций.

При синтезе фазовых корректоров
задаются характеристика ГВП корректируемой цепи, сопротивление нагрузки ![]() ,
точность коррекции и диапазон частот
,
точность коррекции и диапазон частот ![]() ,
в котором осуществляется коррекция. Вначале определяют требуемую характеристику
фазового корректора. Для этого задают постоянное значение ГВП
,
в котором осуществляется коррекция. Вначале определяют требуемую характеристику
фазового корректора. Для этого задают постоянное значение ГВП ![]() ,
которое должно быть несколько больше максимального значения ГВП цепи (рис. 4.6,
б):
,
которое должно быть несколько больше максимального значения ГВП цепи (рис. 4.6,
б):
![]() .
.
Затем любым способом определяют
площадь ![]() под
характеристикой требуемого ГВП корректора, например, площадь можно рассчитать
по формуле
под
характеристикой требуемого ГВП корректора, например, площадь можно рассчитать
по формуле
 .
.
После этого приближенно можно определить число фазовых звеньев второго порядка, необходимых для коррекции, так как площадь под кривой группового времени фазового звена второго порядка равна 2p
![]() .
.
В данной формуле коэффициентом 1.1 учитывается то, что не вся площадь под характеристикой фазового звена попадает в диапазон коррекции.
Зная число звеньев, задаемся в
первом приближении их параметрами ![]() и
и
![]() , k
= 1 ... n. Для начала частоты распределяются равномерно, добротность
определяют из условия требуемой величины группового времени звена на частоте
, k
= 1 ... n. Для начала частоты распределяются равномерно, добротность
определяют из условия требуемой величины группового времени звена на частоте
![]() . Эта величина
выбирается на 10 ... 20% меньше, чем требуемое групповое время корректора на
этой частоте. Из сказанного и формулы (4.17) следует
. Эта величина
выбирается на 10 ... 20% меньше, чем требуемое групповое время корректора на
этой частоте. Из сказанного и формулы (4.17) следует
![]() ,
,
где m = 0,8 ... 0,9.
На рис. 4.18 показаны характеристики ГВП четырех фазовых звеньев, требуемая и реальная характеристики ГВП корректора.
Рис. 4.18
Далее с применением компьютерных программ решается оптимизационная задача в общей постановке:
![]() .
.
Если полученный минимум меньше
или равен требуемой точности коррекции, то по заданным ![]() и
и
![]() рассчитывают
элементы
рассчитывают
элементы ![]() и
и
![]() мостовой схемы
фазового звена (рис. 4.9, а). Остальные элементы находят из условия,
что двухполюсники
мостовой схемы
фазового звена (рис. 4.9, а). Остальные элементы находят из условия,
что двухполюсники ![]() и
и
![]() обратные:
обратные:
![]() .
.
Если полученная точность коррекции не удовлетворяет требованиям, то увеличивают число звеньев и повторяют расчет также с помощью компьютера.
Примеры к главе 4
Пример 4.1
Фазовый корректор (рис. 4.8, а)
имеет элементы ![]() =
100 мГн,
=
100 мГн, ![]() =
500 Ом. Рассчитать и построить графики частотных зависимостей фазовой постоянной
=
500 Ом. Рассчитать и построить графики частотных зависимостей фазовой постоянной
![]() и группового
времени прохождения
и группового
времени прохождения ![]() в
диапазоне частот от 0 до 10 кГц.
в
диапазоне частот от 0 до 10 кГц.
Фазовая характеристика ![]() рассчитывается
по формуле (4.10), поэтому
рассчитывается
по формуле (4.10), поэтому
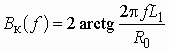 .
.
ГВП ![]() рассчитывается
по формуле (4.11), поэтому
рассчитывается
по формуле (4.11), поэтому
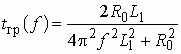 .
.
Подставляя в выражения для ![]() и
и
![]() значения
значения ![]() =
=
![]() Гн и
Гн и ![]() =
500Ом, получаем
=
500Ом, получаем
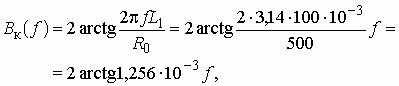
Таблица 4.1
|
f, кГц |
0 |
1 |
2 |
4 |
6 |
8 |
10 |
|
|
0 |
1,8 |
2,38 |
2,75 |
2,88 |
2,94 |
2,98 |
|
|
400 |
155 |
96 |
55 |
38 |
29 |
24 |
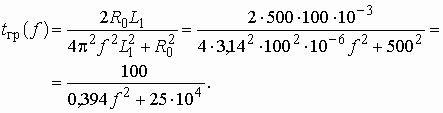
Результаты расчета ![]() и
и
![]() в диапазоне
частот f = = 0 ё 10 кГц приведены в таблице 4.1, а графики – на
рис. 4.10, а и 4.10, б.
в диапазоне
частот f = = 0 ё 10 кГц приведены в таблице 4.1, а графики – на
рис. 4.10, а и 4.10, б.
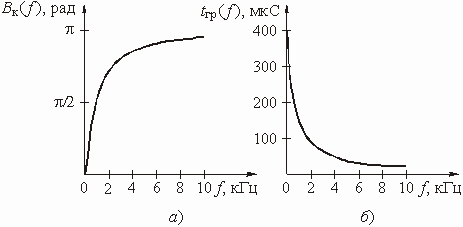
Рис. 4.10
Пример 4.2
Схема фазового корректора приведена
на рис. 4.9, а. Рассчитать и построить графики частотных зависимостей
фазовой постоянной ![]() и
ГВП
и
ГВП ![]() в диапазоне
частот от 0 до 10 кГц для двух случаев:
в диапазоне
частот от 0 до 10 кГц для двух случаев:
 =
600 Ом;
=
600 Ом; 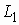 =
36 мГн,
=
36 мГн, 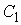 =
0,025 мкФ;
=
0,025 мкФ;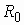 =
600 Ом;
=
600 Ом; 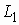 =
36 мГн,
=
36 мГн, 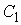
= 0,05 мкФ.
Фазовая характеристика ![]() корректора
рассчитывается по формуле (4.13), а ГВП
корректора
рассчитывается по формуле (4.13), а ГВП ![]() по
формуле (4.14), поэтому
по
формуле (4.14), поэтому
![]() ,
,
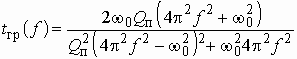 ,
,
где 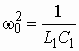 ,
,
![]() .
.
Рассчитаем значения ![]() и
и
![]() для двух случаев
задания параметров элементов корректора:
для двух случаев
задания параметров элементов корректора:
(рад/с)2;
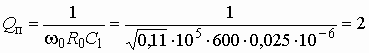 .
.
(рад/с)2;
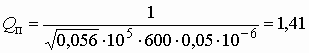 .
.
Подставляя значения ![]() и
и
![]() в выражения
для расчета
в выражения
для расчета ![]() и
и
![]() , рассчитываем
эти характеристики в диапазоне частот от 0 до 10 кГц и заносим результаты расчета
в таблицу 4.2 для случая 1) и в таблицу 4.3 для случая 2).
, рассчитываем
эти характеристики в диапазоне частот от 0 до 10 кГц и заносим результаты расчета
в таблицу 4.2 для случая 1) и в таблицу 4.3 для случая 2).
Поскольку график ![]() имеет
максимум (рис. 4.9, в), то для определения частоты этого максимума берем
производную
имеет
максимум (рис. 4.9, в), то для определения частоты этого максимума берем
производную ![]() и,
приравняв ее к нулю, находим
и,
приравняв ее к нулю, находим
![]() (4.17)
(4.17)
или ![]() для
первого случая (
для
первого случая (![]() =
2) и
=
2) и ![]() = 2,42
кГц для второго случая (
= 2,42
кГц для второго случая (![]() =1,41).
=1,41).
В общем случае анализ выражения
(4.17) показывает, что при ![]() Х
Х
![]() ГВП имеет
максимум на частоте f =0, а при
ГВП имеет
максимум на частоте f =0, а при ![]() <
<
![]() = 1,73 максимум ГВП – на частоте
= 1,73 максимум ГВП – на частоте
![]() .
.
Значение ![]() рассчитывается
по формуле
рассчитывается
по формуле
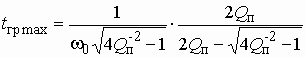 . (4.18)
. (4.18)
Для второго случая, когда Q
= 1,41, имеем ![]() =
144 мкС. Следует также отметить, что при
=
144 мкС. Следует также отметить, что при ![]() .
1 формулы (4.17) и (4.18) существенно упрощаются:
.
1 формулы (4.17) и (4.18) существенно упрощаются:
 . (4.19)
. (4.19)
Таблица 4.2
|
f, кГц |
0 |
2 |
4 |
5,3 |
8 |
10 |
||||||
|
|
0 |
1,44 |
2,59 |
3,14 |
4,11 |
4,35 |
||||||
|
|
120 |
106 |
73,5 |
60 |
34,8 |
26,2 |
||||||
Таблица 4.3
|
f, кГц |
0 |
1 |
2,42 |
3,76 |
6 |
8 |
10 |
|||||
|
|
0 |
0,77 |
2,0 |
3,14 |
4,35 |
4,87 |
5,19 |
|||||
|
|
120 |
117 |
144 |
120 |
57,6 |
30,8 |
18,9 |
|||||
Графики зависимостей ![]() и
и
![]() для двух случаев
приведены на рис. 4.11 (обозначены цифрами 1 и 2).
для двух случаев
приведены на рис. 4.11 (обозначены цифрами 1 и 2).
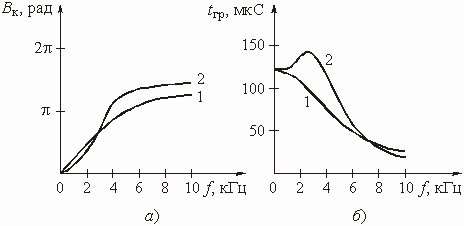
Рис. 4.11
Пример 4.3
Определить передаточную функцию
фазового корректора, построенного по схеме рис. 4.13, в которой в качестве двухполюсника
Z используется параллельный LC-контур. Рассчитать и построить
качественно частотную характеристику ГВП ![]() корректора
в диапазоне частот от 0 до 5 кГц для элементов цепи
корректора
в диапазоне частот от 0 до 5 кГц для элементов цепи ![]() =
37,5 Ом, L = 36 мГн, C = 1,6 мкФ.
=
37,5 Ом, L = 36 мГн, C = 1,6 мкФ.
Найдем сопротивление ![]() параллельного
LC-контура:
параллельного
LC-контура:
 .
.
Подставив ![]() в
формулу (4.21), получим передаточную функцию фазового корректора
в
формулу (4.21), получим передаточную функцию фазового корректора
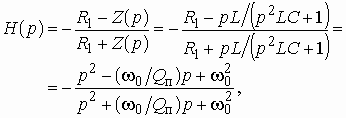
где ![]() ,
,
![]() .
.
ГВП рассчитывается по формуле (4.14),
в которой ![]() ,
,
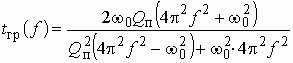 .
.
Находим значения ![]() и
и
![]() :
:
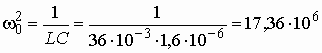 (рад/с)2,
(рад/с)2,
![]() рад/с,
рад/с,
![]() кГц,
кГц,
![]() .
.
Поскольку ![]() ,
то находим значения
,
то находим значения ![]() и
и
![]() по формулам
(3.17) и (3.18):
по формулам
(3.17) и (3.18):
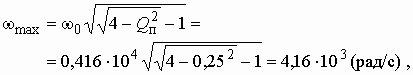
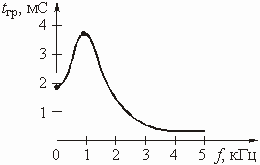
Рис. 4.17
![]() кГц,
кГц,
![]() = 3,7 мС.
= 3,7 мС.
Рассчитываем значения ![]() на
частотах
на
частотах ![]() =
0 и
=
0 и ![]() = 5 кГц
по формуле (4.14). Получаем
= 5 кГц
по формуле (4.14). Получаем ![]() =
1,92 мС и
=
1,92 мС и ![]() =
0,12 мС.
=
0,12 мС.
График зависимости ![]() приведен
на рис. 4.17.
приведен
на рис. 4.17.
Вопросы и задания для самопроверки
1. Сформулировать условия безискаженной передачи сигнала.
2. Почему происходят фазо-частотные искажения?
3. Что такое групповое время прохождения?
4. По рис. 4.6 пояснить, как работает фазовый корректор.
5. Каким образом строятся пассивные фазовые корректоры?
6. Как рассчитываются передаточные
функции ![]() , фазовые
характеристики
, фазовые
характеристики ![]() и
ГВП
и
ГВП ![]() мостовых
фазовых корректоров 1-го и 2-го порядков?
мостовых
фазовых корректоров 1-го и 2-го порядков?
7. Как изменится график ![]() в
Примере 4.1, если индуктивность
в
Примере 4.1, если индуктивность ![]() уменьшить
в 2 раза.
уменьшить
в 2 раза.
8. Определить параметры элементов
фазового корректора 2-го порядка (рис. 4.9) по заданным коэффициентам передаточной
функции ![]()
![]() ,
, ![]() =
0,25 и
=
0,25 и ![]() =
600 Ом.
=
600 Ом.
Ответ:
![]() =
36 мГн;
=
36 мГн; ![]() =
1,6 мкФ;
=
1,6 мкФ; ![]() =
0,58 Гн;
=
0,58 Гн; ![]() =
0,1 мкФ.
=
0,1 мкФ.
9. Каким образом строятся активные фазовые корректоры?
10. Доказать, что операторная
передаточная функция ![]() корректора,
изображенного на рис. 4.13, имеет вид (4.20).
корректора,
изображенного на рис. 4.13, имеет вид (4.20).
11. Каким образом на основе схемы рис. 4.15 получить фазовые корректоры 1-го и 2-го порядков?
12. Как изменится график ![]() в
Примере 4.3, если сопротивление
в
Примере 4.3, если сопротивление ![]() : 1) увеличить в 4 раза; 2)
увеличить в 10 раз; 3) уменьшить в 2 раза?
: 1) увеличить в 4 раза; 2)
увеличить в 10 раз; 3) уменьшить в 2 раза?
13. Каков алгоритм расчета фазовых корректоров?
Глава 5. Нелинейные преобразователи

Для линейного резистивного элемента R существует прямая пропорциональная зависимость между протекающим через этот элемент током i и приложенным к нему напряжение u (рис. 5.1):
![]() или
или
![]() . (5.1)
. (5.1)
Уравнение (5.1) называется вольт-амперной характеристикой (ВАХ) резистивного элемента. Так как R постоянно, то ВАХ линейна.
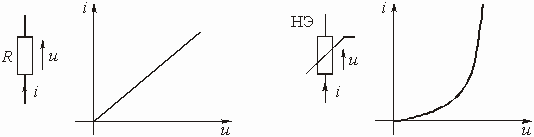
Рис. 5.1 Рис. 5.2
Для нелинейного резистивного элемента характерна нелинейная связь между током i и напряжением u (рис. 5.2). Сопротивление нелинейного резистивного элемента (НЭ) не является постоянным, а зависит от того, в какой точке ВАХ оно определяется. На рис. 5.3 изображена ВАХ нелинейного элемента. Можно определить сопротивление как
![]() ,
,
где ![]() –
приложенное к нелинейному элементу постоянное напряжение;
–
приложенное к нелинейному элементу постоянное напряжение; ![]() –
протекающий через нелинейный элемент постоянный ток. Это сопротивление постоянному
току (или статическое). Оно зависит от приложенного напряжения.
–
протекающий через нелинейный элемент постоянный ток. Это сопротивление постоянному
току (или статическое). Оно зависит от приложенного напряжения.
Пусть на нелинейный элемент действует
сумма постоянного напряжения ![]() и
гармонического
и
гармонического ![]() ,
причем амплитуда
,
причем амплитуда ![]() переменной
составляющей достаточно мала (рис. 5.3), так что тот небольшой участок ВАХ,
в пределах которого действует переменное напряжение, можно считать линейным.
Проектируя каждое мгновенное значение гармонического напряжения на ВАХ и отображая
результат проекции на плоскости “ ток – время” , получим зависимость тока от
времени. В силу того, что выбран линейный участок ВАХ ток, протекающий через
нелинейный элемент, повторит по форме напряжение:
переменной
составляющей достаточно мала (рис. 5.3), так что тот небольшой участок ВАХ,
в пределах которого действует переменное напряжение, можно считать линейным.
Проектируя каждое мгновенное значение гармонического напряжения на ВАХ и отображая
результат проекции на плоскости “ ток – время” , получим зависимость тока от
времени. В силу того, что выбран линейный участок ВАХ ток, протекающий через
нелинейный элемент, повторит по форме напряжение: ![]() (рис.
5.3). Отношение амплитуды переменного напряжения
(рис.
5.3). Отношение амплитуды переменного напряжения ![]() к
амплитуде переменного тока
к
амплитуде переменного тока ![]() (на
графике это отношение приращения напряжения
(на
графике это отношение приращения напряжения ![]() к
приращению тока
к
приращению тока ![]() )
называют дифференциальным (динамическим) сопротивлением нелинейного элемента,
которое, по сути, является сопротивлением нелинейного элемента переменному
току малой амплитуды:
)
называют дифференциальным (динамическим) сопротивлением нелинейного элемента,
которое, по сути, является сопротивлением нелинейного элемента переменному
току малой амплитуды:
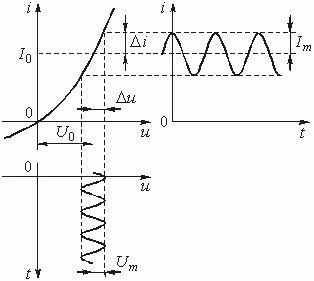
Рис. 5.3
![]() .
.
Обычно переходят к пределу этих
приращений и определяют дифференциальное сопротивление в виде ![]() .
Часто удобно пользоваться понятием дифференциальной крутизны (проводимости):
.
Часто удобно пользоваться понятием дифференциальной крутизны (проводимости):
![]() .
.
Наиболее распространенными приборами
с нелинейным резистивным сопротивлением являются ламповые и полупроводниковые
приборы (диоды, транзисторы и т. п.), используемые в радиотехнике для преобразования
и усиления сигналов. На рис. 5.4 приведены ВАХ типовых нелинейных резисторов
и их условные обозначения: полупроводникового (а) и туннельного (б)
диодов; биполярного (в) и полевого (г) транзисторов. Здесь ![]() ,
,
![]() и
и ![]() –
соответственно напряжение, приложенное к участку “ база – эмиттер” , и токи
базы и коллектора биполярного транзистора;
–
соответственно напряжение, приложенное к участку “ база – эмиттер” , и токи
базы и коллектора биполярного транзистора; ![]() и
и
![]() – соответственно
напряжение, приложенное к участку “ затвор – исток” и ток стока полевого транзистора.
– соответственно
напряжение, приложенное к участку “ затвор – исток” и ток стока полевого транзистора.
Рис. 5.4
Приборы, имеющие падающие участки
ВАХ (см. рис. 5.4, б), называются приборами с отрицательным сопротивлением,
т.к. ![]() .
.

Расчет нелинейных цепей, ВАХ нелинейных элементов (НЭ) которых заданы графически или описываются сложными функциями, проводят графоаналитическими методами. Суть этих методов состоит в составлении системы аналитических уравнений, которые затем решаются графически. Точки пересечения графиков дают искомое решение.
Для расчета цепи, содержащей один НЭ, естественно применить метод эквивалентного генератора, при этом линейная цепь относительно зажимов НЭ заменяется эквивалентным генератором напряжения или тока (рис. 5.5).
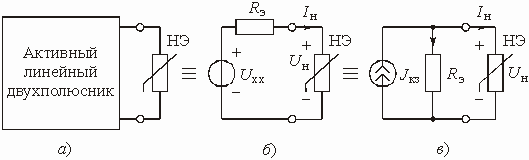
Рис. 5.5
Напомним, что параметры эквивалентного
генератора определяют следующим образом: ![]() –
напряжение на зажимах активного линейного двухполюсника (АЛД) при отключенном
НЭ;
–
напряжение на зажимах активного линейного двухполюсника (АЛД) при отключенном
НЭ; ![]() – эквивалентное
сопротивление пассивного двухполюсника, когда все задающие напряжения и токи
источников АЛД равны нулю;
– эквивалентное
сопротивление пассивного двухполюсника, когда все задающие напряжения и токи
источников АЛД равны нулю; ![]() –
ток АЛД при коротком замыкании его зажимов.
–
ток АЛД при коротком замыкании его зажимов.
Ток в НЭ и напряжение на нем находятся из системы, состоящей всего из двух уравнений. Так, применяя закон напряжений Кирхгофа (ЗНК) к схеме рис. 5.5, б, получаем:
![]() . (5.2)
. (5.2)
Дописывая к данному равенству уравнение
НЭ ![]() , получаем
систему из двух уравнений. Решить данную систему можно графическим путем, построив
график прямой
, получаем
систему из двух уравнений. Решить данную систему можно графическим путем, построив
график прямой
 (5.3)
(5.3)
и график ВАХ ![]() нелинейного
элемента. Точка пересечения графиков дает значение тока
нелинейного
элемента. Точка пересечения графиков дает значение тока ![]() и
напряжения
и
напряжения ![]() на
НЭ (рис. 5.6).
на
НЭ (рис. 5.6).
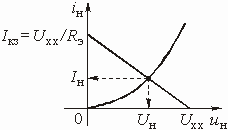
Рис. 5.6
Все остальные токи и напряжения на линейных элементах можно найти, используя законы Кирхгофа.
Для расчета цепи, содержащей несколько НЭ, используют эквивалентные преобразования схемы. Суть эквивалентных преобразований состоит в замене участков цепи с параллельным или последовательным соединением ветвей одной эквивалентной ветвью путем суммирования их токов или напряжений. Речь здесь идет о суммировании ординат или абсцисс заданных характеристик ветвей цепи. Этот метод особенно эффективен в случае цепи с одним источником: цепь представляется источником и одним эквивалентным нелинейным элементом.
Пусть два НЭ с уравнениями (ВАХ)
![]() и
и ![]() включены
параллельно (рис. 5.9). Поскольку приводимые ниже рассуждения справедливы не
только для режима постоянного, но и для режима переменного тока, в дальнейшем
будем использовать для обозначений напряжений и токов малые (строчные) буквы.
включены
параллельно (рис. 5.9). Поскольку приводимые ниже рассуждения справедливы не
только для режима постоянного, но и для режима переменного тока, в дальнейшем
будем использовать для обозначений напряжений и токов малые (строчные) буквы.
Необходимо найти уравнение НЭ,
эквивалентного данному соединению элементов. Так как элементы соединены параллельно,
то ![]()
![]() ,
а по первому закону Кирхгофа
,
а по первому закону Кирхгофа ![]() .
Выполним сложение токов графически, как показано на рис. 5.10. Задаемся значением
напряжения. При этом значении напряжения находим токи НЭ и суммируем их. Задаемся
новым значением напряжения и опять суммируем токи. Таким образом, находим серию
точек, соединяя которые, получаем ВАХ эквивалентного НЭ.
.
Выполним сложение токов графически, как показано на рис. 5.10. Задаемся значением
напряжения. При этом значении напряжения находим токи НЭ и суммируем их. Задаемся
новым значением напряжения и опять суммируем токи. Таким образом, находим серию
точек, соединяя которые, получаем ВАХ эквивалентного НЭ.
Рис. 5.9 Рис. 5.10
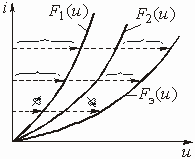
Рис. 5.11 Рис. 5.12
Рассмотрим последовательное соединение
НЭ (рис. 5.11). В данном случае ![]() ,
а
,
а ![]() . Процесс определения
ВАХ НЭ показан на рис. 5.12. Заметим, что рассмотренные преобразования применимы
и в случае, когда последовательно или параллельно соединены несколько нелинейных,
а также линейных элементов.
. Процесс определения
ВАХ НЭ показан на рис. 5.12. Заметим, что рассмотренные преобразования применимы
и в случае, когда последовательно или параллельно соединены несколько нелинейных,
а также линейных элементов.
Если вольт-амперные характеристики
двухполюсных НЭ заданы не графически, а аналитически, причем функции ![]() достаточно
простые, то для расчета нелинейных цепей составляют систему уравнений состояния
цепи, которую решают аналитически или численными методами.
достаточно
простые, то для расчета нелинейных цепей составляют систему уравнений состояния
цепи, которую решают аналитически или численными методами.
Уравнения состояния цепи обычно
составляют на основании законов Кирхгофа. Методика составления уравнений остается
такой же, как и в случае линейных резистивных цепей, но дополнительно появляются
уравнения вида ![]() для
НЭ.
для
НЭ.
Составим, например, систему уравнений состояния для цепи, схема которой изображена на рис. 5.17. Пусть ВАХ нелинейного элемента описывается выражением
Рис. 5.17
 (5.4)
(5.4)
Зададимся положительными направлениями напряжений и токов. Цепь содержит один независимый контур (I) и один независимый узел (1). Уравнения, записанные по закону токов Кирхгофа (ЗТК) и ЗНК, имеют следующий вид:
![]() ;
(5.5)
;
(5.5)
![]() .
(5.6)
.
(5.6)
К этим уравнениям дописываем
уравнение (5.4). Неизвестными в данной системе уравнений являются напряжение
![]() и токи
и токи ![]() и
и
![]() . Всего три
неизвестных. Для их отыскания составлено три уравнения. Как видим, процесс
составления системы уравнений такой же, как и в случае линейной цепи. Однако
процесс решения полученной системы, которая содержит нелинейное уравнение,
может существенно затрудниться. Для большинства относительно сложных цепей
аналитического решения системы уравнений может и не существовать. Тогда приходится
прибегать к численным методам решения.
. Всего три
неизвестных. Для их отыскания составлено три уравнения. Как видим, процесс
составления системы уравнений такой же, как и в случае линейной цепи. Однако
процесс решения полученной системы, которая содержит нелинейное уравнение,
может существенно затрудниться. Для большинства относительно сложных цепей
аналитического решения системы уравнений может и не существовать. Тогда приходится
прибегать к численным методам решения.
Можно составлять уравнения состояния цепи методом узловых напряжений (потенциалов).
Рассмотрим в качестве примера схему,
изображенную на рис. 5.18. Пусть ВАХ нелинейных элементов описываются выражениями
![]() для элемента НЭ1
и
для элемента НЭ1
и ![]() для элемента
НЭ2. В схеме имеется зависимый источник (ИТУТ) с током
для элемента
НЭ2. В схеме имеется зависимый источник (ИТУТ) с током ![]() .
.
Рис. 5.18
Приняв узел 4 за базисный, имеем
три независимых узла: 1, 2 и 3. Токи ветвей выражаются через узловые напряжения
![]() ,
, ![]() и
и
![]() следующим образом:
следующим образом:
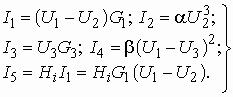 (5.11)
(5.11)
Составим уравнения для узлов 1, 2 и 3 по ЗТК:
![]() ;
;
![]() ;
;
![]() .
.
Подставив в эти уравнения значения токов из (5.11), получим
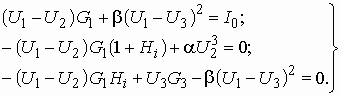 (5.12)
(5.12)
Уравнения узловых напряжений получены
в виде системы трех нелинейных уравнений с тремя неизвестными узловыми напряжениями.
Можно уменьшить число уравнений, если из первого уравнения выразить ![]() через
через
![]() и
и ![]() и
исключить его из двух остальных уравнений. В результате получим систему двух
нелинейных уравнений с двумя неизвестными напряжениями узлов 1 и 3.
и
исключить его из двух остальных уравнений. В результате получим систему двух
нелинейных уравнений с двумя неизвестными напряжениями узлов 1 и 3.
Решить данную систему уравнений можно одним из численных методов (например, известным из математики методом Ньютона – Рафсона). Определив узловые напряжения, можно вычислить токи и напряжения ветвей.
Рассмотрим порядок расчета резистивных
цепей, если в их состав входят нелинейные четырехполюсники, которые описываются
нелинейными уравнениями, связывающими напряжения и токи на его входе (![]() ,
,
![]() ) и выходе (
) и выходе (![]() ,
,
![]() ):
):
![]() ;
;
![]() .
.
На рис. 5.19 показана схема включения нелинейного четырехполюсника, а на рис. 5.20 – семейство его входных (а) и выходных (б) ВАХ.
По ЗНК для входной и выходной цепей схемы рис. 5.19 можно записать:
![]() и
и
![]() .
.

Рис. 5.19
Решая эти уравнения относительно
токов ![]() и
и ![]() ,
получаем уравнения
,
получаем уравнения
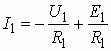 и
и
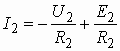 ,
,
которые называются уравнениями нагрузочных прямых.
На рис. 5.20 построены графики этих прямых и графических входных и выходных ВАХ четырехполюсного НЭ. Точки пересечения нагрузочных прямых и ВАХ определяют режимы постоянного тока (рабочие точки) на входе и выходе четырехполюсного НЭ.
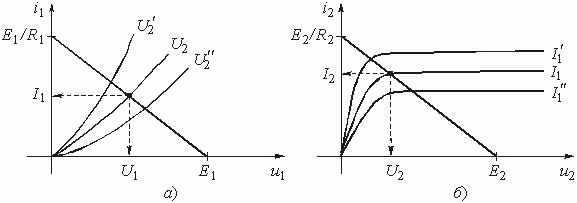
Рис. 5.20

Как правило, ВАХ нелинейных элементов получают экспериментально, поэтому чаще всего они заданы в виде таблиц или графиков. Чтобы иметь дело с аналитическими выражениями, приходится прибегать к аппроксимации.
На рис. 5.21 приведена ВАХ нелинейного
элемента. Пусть к нелинейному элементу приложено постоянное напряжение ![]() и
гармоническое напряжение
и
гармоническое напряжение ![]() .
.
Рис. 5.21
Увеличение величины постоянного
напряжения ![]() приведет
к смещению на рис. 5.21 гармонического напряжения вправо, а уменьшение
приведет
к смещению на рис. 5.21 гармонического напряжения вправо, а уменьшение ![]() –
к смещению гармонического напряжения влево. В связи с этим постоянное напряжение
–
к смещению гармонического напряжения влево. В связи с этим постоянное напряжение
![]() назвали напряжением
смещения, а точку на ВАХ с координатами (
назвали напряжением
смещения, а точку на ВАХ с координатами (![]() ,
,![]() )
– рабочей точкой. Таким образом, выбор рабочей точки на ВАХ связан с
изменением напряжения смещения
)
– рабочей точкой. Таким образом, выбор рабочей точки на ВАХ связан с
изменением напряжения смещения ![]() .
.
При подаче на нелинейный элемент гармонического напряжения рабочая точка будет перемещаться по ВАХ в такт с изменением мгновенного значения гармонического напряжения.
Очевидно, что аппроксимировать (т. е. описывать аналитически) нужно только тот участок ВАХ, по которому перемещается рабочая точка.
Часто в качестве аппроксимирующего ВАХ выражения используют степенной полином:
![]() . (5.13)
. (5.13)
Определить коэффициенты ![]() ,
,
![]() , ... ,
, ... , ![]() полинома
(5.13) можно различными способами. Наиболее распространенным способом является
интерполяция (метод выбранных точек), при которой коэффициенты
полинома
(5.13) можно различными способами. Наиболее распространенным способом является
интерполяция (метод выбранных точек), при которой коэффициенты ![]() ,
,
![]() , ... ,
, ... , ![]() находятся
из равенства значений полинома (5.13) и аппроксимируемой ВАХ в выбранных точках
(узлах интерполяции).
находятся
из равенства значений полинома (5.13) и аппроксимируемой ВАХ в выбранных точках
(узлах интерполяции).

Прежде всего следует уточнить,
что понимается под большой амплитудой гармонического напряжения. На рис. 5.23
кружочками, соединенными пунктирной линией, показана экспериментальная зависимость
тока базы ![]() от напряжения
от напряжения
![]() , полученная для
транзистора КТ-306. Кроме того, известно, что напряжение смещения выбрано равным
, полученная для
транзистора КТ-306. Кроме того, известно, что напряжение смещения выбрано равным
![]() , а гармонический
сигнал, также подводимый к нелинейному элементу, имеет амплитуду
, а гармонический
сигнал, также подводимый к нелинейному элементу, имеет амплитуду ![]() (рис.
5.23).
(рис.
5.23).
Из графика видно, что когда мгновенное
значение гармонического напряжения изменяется от –0,3 до –0,6 В, напряжение
на участке “ база – эмиттер” становится отрицательным и ток базы отсутствует
(![]() = 0), т. е.
транзистор “ закрыт” . По-видимому, в данном случае как раз и можно говорить
о большой амплитуде сигнала на входе транзистора.
= 0), т. е.
транзистор “ закрыт” . По-видимому, в данном случае как раз и можно говорить
о большой амплитуде сигнала на входе транзистора.
С некоторым приближением можно
считать, что ВАХ транзистора имеет два участка: первый – там, где ток базы ![]() =
0 (при
=
0 (при ![]() ) и транзистор
“ закрыт” ; второй – там, где ток базы растет с ростом напряжения
) и транзистор
“ закрыт” ; второй – там, где ток базы растет с ростом напряжения ![]() и,
следовательно, транзистор “ открыт” . При этом можно пренебречь “ кривизной”
вольт-амперной характеристики и заменить ее на втором участке прямой линией.
На рис. 5.23 аппроксимирующая ВАХ прямая линия изображена сплошной линией. Такой
же сплошной линией показана зависимость тока базы от времени, полученная путем
проекции гармонического напряжения на аппроксимирующую ВАХ прямую линию. Для
сравнения пунктиром показан реальный ток базы, протекающий через нелинейный
элемент с экспериментальной ВАХ. Поскольку отличие этих кривых незначительное,
можно считать замену ВАХ прямой линией вполне приемлемой.
и,
следовательно, транзистор “ открыт” . При этом можно пренебречь “ кривизной”
вольт-амперной характеристики и заменить ее на втором участке прямой линией.
На рис. 5.23 аппроксимирующая ВАХ прямая линия изображена сплошной линией. Такой
же сплошной линией показана зависимость тока базы от времени, полученная путем
проекции гармонического напряжения на аппроксимирующую ВАХ прямую линию. Для
сравнения пунктиром показан реальный ток базы, протекающий через нелинейный
элемент с экспериментальной ВАХ. Поскольку отличие этих кривых незначительное,
можно считать замену ВАХ прямой линией вполне приемлемой.
Рис. 5.23
Уравнение прямой линии имеет вид:
![]() , где К
– коэффициент, определяющий наклон прямой. Смещение прямой параллельно самой
себе вправо оси абсцисс на величину
, где К
– коэффициент, определяющий наклон прямой. Смещение прямой параллельно самой
себе вправо оси абсцисс на величину ![]() описывается
выражением:
описывается
выражением:
![]() .
.
Наклон аппроксимирующей ВАХ прямой
линии определяется крутизной S, а смещение по оси ![]() –
напряжением отсечки
–
напряжением отсечки ![]() .
Аппроксимирующая ВАХ функция задается параметрически для двух участков напряжения
.
Аппроксимирующая ВАХ функция задается параметрически для двух участков напряжения
![]() (рис. 5.23):
(рис. 5.23):
![]() (5.17)
(5.17)
Для экспериментальных данных, приведенных
на рис. 5.23, крутизна S определяется приращением тока ![]() к
приращению напряжения
к
приращению напряжения ![]() и
составляет 4 мА/В, а напряжение отсечки
и
составляет 4 мА/В, а напряжение отсечки ![]() равно
0,5 В.
равно
0,5 В.

Рассмотрим схему усилительного
каскада на биполярном транзисторе (рис. 5.25), на входе которого действует напряжение
![]() , состоящее из
напряжения смещения
, состоящее из
напряжения смещения ![]() и
гармонического напряжения с амплитудой
и
гармонического напряжения с амплитудой ![]() .
Под действием входного напряжения в цепи коллектора транзистора протекает коллекторный
ток
.
Под действием входного напряжения в цепи коллектора транзистора протекает коллекторный
ток ![]() . Зависимость
коллекторного тока от напряжения на участке “ база – эмиттер” является проходной
вольт-амперной характеристикой.
. Зависимость
коллекторного тока от напряжения на участке “ база – эмиттер” является проходной
вольт-амперной характеристикой.
Рис. 5.25
На рис. 5.26 изображены проходная
ВАХ транзисторного каскада, зависимость во времени напряжения на входе каскада
![]() и зависимость
во времени коллекторного тока
и зависимость
во времени коллекторного тока ![]() .
Напряжение смещения
.
Напряжение смещения ![]() и
амплитуда гармонического напряжения
и
амплитуда гармонического напряжения ![]() выбраны
на рисунке таким образом, что рабочая точка не выходит за пределы линейного
участка ВАХ. В результате коллекторный ток будет содержать постоянную составляющую
выбраны
на рисунке таким образом, что рабочая точка не выходит за пределы линейного
участка ВАХ. В результате коллекторный ток будет содержать постоянную составляющую
![]() и гармоническую
составляющую с амплитудой
и гармоническую
составляющую с амплитудой ![]() .
.
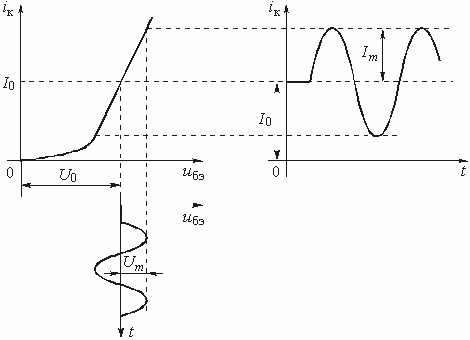
Рис. 5.26
Иная картина будет наблюдаться,
если напряжение смещения ![]() уменьшить
и, тем самым, выбрать рабочую точку на нижнем, нелинейном, участке ВАХ (рис.
5.27). Форма тока исказится, ток перестанет быть гармоническим. Дальнейшее уменьшение
напряжения смещения
уменьшить
и, тем самым, выбрать рабочую точку на нижнем, нелинейном, участке ВАХ (рис.
5.27). Форма тока исказится, ток перестанет быть гармоническим. Дальнейшее уменьшение
напряжения смещения ![]() приведет
к еще большему искажению формы тока (рис. 5.28).
приведет
к еще большему искажению формы тока (рис. 5.28).
Из теории спектрального анализа
сигналов известно, что любой периодический сигнал может быть представлен рядом
Фурье. Это значит, что коллекторный ток ![]() складывается
из постоянной составляющей, основной составляющей с частотой входного сигнала
и высших гармоник:
складывается
из постоянной составляющей, основной составляющей с частотой входного сигнала
и высших гармоник:
![]() . (5.18)
. (5.18)
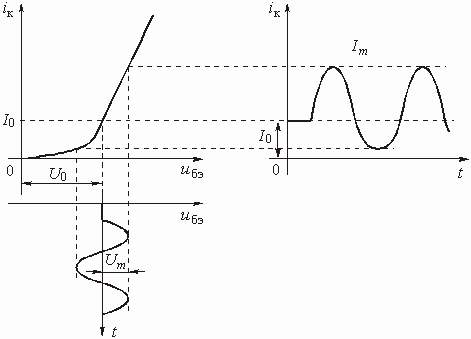
Рис. 5.27
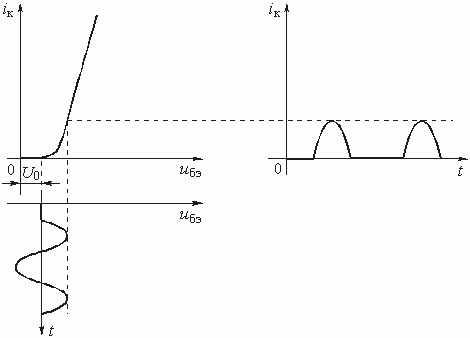
Рис. 5.28
Искажения формы сигнала из-за нелинейности ВАХ называют нелинейными искажениями. Если перед нами стоит задача усилить сигнал без искажений (например, при воспроизведении речи, музыки, изображения и т. п.), то следует выбирать такой режим работы (напряжение смещения и амплитуды сигналов), чтобы не выходить за пределы линейного участка ВАХ.
Наоборот, стремление преобразовать сигнал с помощью нелинейного элемента, например, не дать мгновенному значению сигнала превысить некоторый заранее установленный порог, приводит к необходимости работать в режиме больших нелинейных искажений.
На рис. 5.29 изображена вольт-амперная характеристика диода. Приближенно можно считать, что при воздействии на диод напряжения в “ прямом направлении” (правая полуплоскость рисунка) через него будет протекать ток, т. е. р-n переход диода будет открыт, а при воздействии напряжения в “ обратном направлении” (левая полуплоскость рисунка) ток практически протекать не будет, т. е. p-n переход диода будет закрыт.
Рис. 5.29
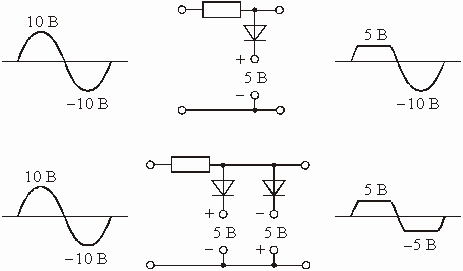
Рис. 5.30
На практике широко применяются
схемы диодных ограничителей напряжения (рис. 5.30). Здесь диод выполняет роль
вентиля: в открытом состоянии его сопротивление мало (десятки Ом), в закрытом
состоянии – очень велико (сотни МОм). Эти свойства диода позволяют аппроксимировать
его ВАХ кусочно-линейной функцией (рис. 5.31). Напряжением смещения ![]() регулируют
порог ограничения.
регулируют
порог ограничения.
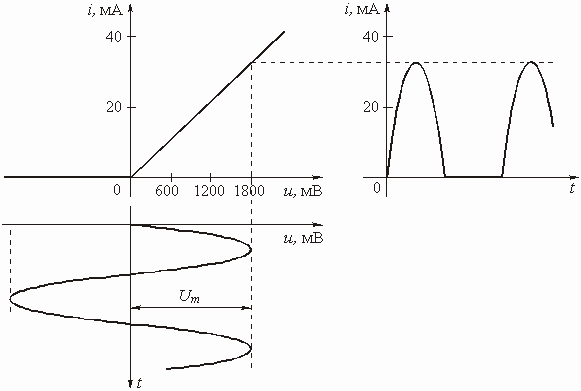
Рис. 5.31

Ограничимся рассмотрением полиномов со степенью не выше третьей.
График полинома первой степени
![]() (5.19)
(5.19)
представляет собой прямую ![]() ,
параллельную оси абсцисс, и наклонную прямую
,
параллельную оси абсцисс, и наклонную прямую ![]() с
коэффициентом наклона
с
коэффициентом наклона ![]() ,
смещенную по оси абсцисс на величину
,
смещенную по оси абсцисс на величину ![]() .
Регулируя величины
.
Регулируя величины ![]() ,
,
![]() и
и ![]() ,
можно перемещать аппроксимирующую прямую вниз, вправо и влево и менять ее наклон.
,
можно перемещать аппроксимирующую прямую вниз, вправо и влево и менять ее наклон.
Для определения амплитуд гармоник
тока подставим в (5.19) выражение для напряжения, приложенного к нелинейному
элементу ![]() :
:
![]() .
.
Сравнивая это выражение с рядом Фурье
![]() ,
,
видим, что ![]() ;
;
![]() ;
; ![]() .
Таким образом, при аппроксимации ВАХ полиномом 1-ой степени ток содержит кроме
постоянной составляющей
.
Таким образом, при аппроксимации ВАХ полиномом 1-ой степени ток содержит кроме
постоянной составляющей ![]() только
основную (первую) гармонику, совпадающую по частоте с приложенным гармоническим
напряжением. Высшие гармоники в спектре тока отсутствуют, нелинейных искажений
нет.
только
основную (первую) гармонику, совпадающую по частоте с приложенным гармоническим
напряжением. Высшие гармоники в спектре тока отсутствуют, нелинейных искажений
нет.
График полинома второй степени
![]() (5.20)
(5.20)
содержит в дополнение к графику
полинома первой степени квадратичную параболу ![]() ,
смещенную по оси абсцисс на величину
,
смещенную по оси абсцисс на величину ![]() .
Квадратичный член служит для аппроксимации слабой нелинейности ВАХ параболического
типа.
.
Квадратичный член служит для аппроксимации слабой нелинейности ВАХ параболического
типа.
Подставляя в (5.20) напряжение
![]() , получим:
, получим:
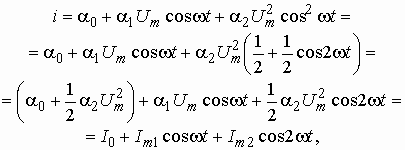
Это выражение показывает, что если вольт-амперная характеристика нелинейного элемента имеет нелинейность, описываемую квадратичной параболой, то в спектре тока, протекающего через такой нелинейный элемент, появляется при воздействии на него постоянного и гармонического напряжений вторая гармоника с частотой 2w .
Для описания нелинейности ВАХ более высокого порядка используется полином третьей степени
![]() , (5.21)
, (5.21)
в котором добавляется так называемая
кубическая парабола ![]() ,
смещенная по оси абсцисс на величину
,
смещенная по оси абсцисс на величину ![]() .
.
В этом случае подстановка напряжения
![]() в
в
(5.21) дает:
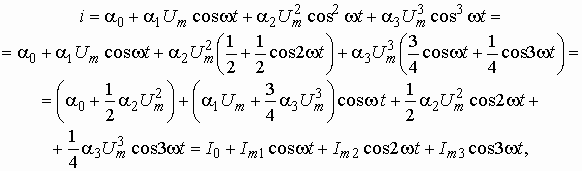
где постоянная составляющая ![]() и
амплитуды гармоник
и
амплитуды гармоник ![]() ,
,
![]() и
и ![]() .
.
Из приведенных примеров видно, что наличие в ВАХ нелинейностей высокого порядка приводит к появлению высших гармоник в спектре тока. Количество гармоник в спектре тока равно степени полинома, описывающего нелинейность ВАХ. Постоянная составляющая и амплитуды четных гармоник определяются коэффициентами полинома при четных степенях, а амплитуды нечетных гармоник – коэффициентами полинома при нечетных степенях. Это означает, что если ВАХ аппроксимируется полиномом только с четными степенями, в спектре тока будут присутствовать постоянная составляющая и четные гармоники. При аппроксимации ВАХ полиномом с нечетными степенями спектр тока будет содержать только нечетные гармоники.

Напомним, что при больших амплитудах гармонического напряжения, подводимого к нелинейному элементу, практически нет смысла учитывать небольшую кривизну ВАХ (так называемую слабую нелинейность). В тех случаях, когда нелинейный элемент работает как вентиль: есть ток или нет тока, используют кусочно-линейную аппроксимацию ВАХ (рис. 5.33):
![]() (5.21)
(5.21)
График тока при этом имеет вид косинусоидальных импульсов с отсечкой. Половина той части периода в радианах (или градусах), в течение которой протекает ток, называется углом отсечки и обозначен на рисунке буквой q .
Из графика рис. 5.33 можно вычислить
угол отсечки q . При ![]() напряжение
напряжение
![]() . Откуда
. Откуда
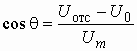 и
и
 . (5.22)
. (5.22)
Рис. 5.33
Последнее равенство показывает,
что угол отсечки можно изменить, меняя напряжение смещения ![]() ,
амплитуду гармонического сигнала
,
амплитуду гармонического сигнала ![]() или
выбирая параметр
или
выбирая параметр ![]() аппроксимирующей
функции (5.21).
аппроксимирующей
функции (5.21).
Периодическую последовательность импульсов тока на рис. 5.33 можно разложить в ряд Фурье:
![]() .
.
Опуская процедуру нахождения коэффициентов ряда Фурье и отсылая любознательного читателя к стандартным учебникам, приведем окончательный результат.
Постоянная составляющая и амплитуды гармоник тока вычисляются по формуле
![]() ,
k = 0, 1, 2, 3, ... , (5.23)
,
k = 0, 1, 2, 3, ... , (5.23)
где функции ![]() называются
функциями Берга (в честь крупного российского радиотехника академика А.И. Берга).
Они зависят от угла отсечки и их значения для разных углов отсечки приводятся
в справочниках. Графики нескольких функций Берга представлены на рис. 5.34.
называются
функциями Берга (в честь крупного российского радиотехника академика А.И. Берга).
Они зависят от угла отсечки и их значения для разных углов отсечки приводятся
в справочниках. Графики нескольких функций Берга представлены на рис. 5.34.
Рис. 5.34
Чтобы получить максимальные амплитуды
гармоник, следует выбирать ![]() ,
так как при таких углах отсечки функции Берга
,
так как при таких углах отсечки функции Берга ![]() принимают
максимальные значения.
принимают
максимальные значения.
Таким образом, амплитуды спектральных составляющих тока в нелинейном элементе при кусочно-линейной аппроксимации его ВАХ зависят от угла отсечки. Количество гармоник при этом бесконечно большое. Чем меньше угол отсечки (т. е. чем уже импульс), тем медленнее убывают амплитуды гармоник тока.

Рассмотрим вначале процессы в
линейном усилителе с резистивной нагрузкой (рис. 5.35, а). Это позволит
лучше уяснить отличия от него нелинейного резонансного усилителя. Будем полагать,
что ВАХ ![]() , т.
е. зависимость тока коллектора от напряжения на участке база – эмиттер, достаточно
точно представляется кусочно-линейной функцией вида (5.21). На входе НЭ транзистора
действует напряжение
, т.
е. зависимость тока коллектора от напряжения на участке база – эмиттер, достаточно
точно представляется кусочно-линейной функцией вида (5.21). На входе НЭ транзистора
действует напряжение
![]() ,
,
не выходящее за пределы линейного участка. Тогда ток в цепи коллектора
![]()
будет, как и входное напряжение, гармоническим (рис. 5.35, б).
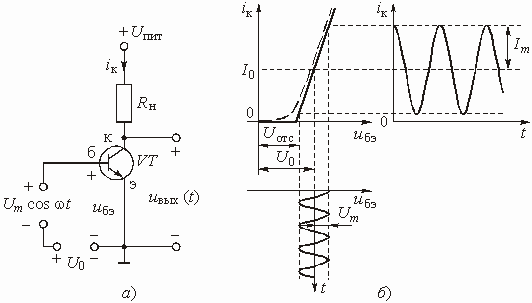
Рис. 5.35
Определим коэффициент полезного
действия (КПД) линейного усилителя. Ток коллектора создает на резисторе нагрузки
![]() падение напряжения
падение напряжения
![]() , которое является
выходным сигналом с амплитудой
, которое является
выходным сигналом с амплитудой ![]() .
КПД усилителя есть отношение полезной активной мощности
.
КПД усилителя есть отношение полезной активной мощности
![]()
к активной мощности, потребляемой
от источника питания ![]() ,
т. е.
,
т. е.
 .
.
Из рис. 5.35, б видно,
что ![]() . Если при
этом учесть, что
. Если при
этом учесть, что ![]() ,
то получим КПД h Ф 0,5, т. е. коэффициент полезного действия линейного усилителя
не может превышать 50%.
,
то получим КПД h Ф 0,5, т. е. коэффициент полезного действия линейного усилителя
не может превышать 50%.
Вольт-амперная характеристика
![]() реальных транзисторов
является нелинейной (на рис. 5.35, б она показана штрихами), поэтому
форма тока в цепи коллектора при гармоническом воздействии на усилитель будет
отличаться от гармонической. В коллекторной цепи оказываются постоянная составляющая,
а также первая, вторая и последующие гармоники частоты сигнала.
реальных транзисторов
является нелинейной (на рис. 5.35, б она показана штрихами), поэтому
форма тока в цепи коллектора при гармоническом воздействии на усилитель будет
отличаться от гармонической. В коллекторной цепи оказываются постоянная составляющая,
а также первая, вторая и последующие гармоники частоты сигнала.
Чтобы количественно оценить степень искажения сигнала на выходе усилителя, вводят коэффициент гармоник, который определяется отношением среднеквадратического уровня всех высших гармоник к амплитуде первой гармоники тока:
![]() .
.
Так работает усилитель в линейном режиме, который в большинстве случаев и используется на практике. Между тем, достаточно мощные усилители выгодно использовать в нелинейном режиме работы, поскольку, как будет показано ниже, они имеют более высокий КПД.
Нелинейный резонансный усилитель
изображен на рис. 5.36. На входе его действует переменное напряжение ![]() и
постоянное напряжение смещения
и
постоянное напряжение смещения ![]() ,
причем амплитуда
,
причем амплитуда ![]() переменного
напряжения велика, так что напряжение
переменного
напряжения велика, так что напряжение ![]() “выходит”
за рамки линейного участка (см. рис. 5.33). Ток в цепи коллектора имеет форму
косинусоидальных импульсов с отсечкой. Резонансный контур настроен на частоту
первой гармоники тока, т. е. на частоту входного сигнала w . Сопротивление
параллельного контура на этой частоте велико, а на частотах гармоник 2w ,
3w , ... мало, так что высшие гармонические составляющие практически не влияют
на форму выходного сигнала
“выходит”
за рамки линейного участка (см. рис. 5.33). Ток в цепи коллектора имеет форму
косинусоидальных импульсов с отсечкой. Резонансный контур настроен на частоту
первой гармоники тока, т. е. на частоту входного сигнала w . Сопротивление
параллельного контура на этой частоте велико, а на частотах гармоник 2w ,
3w , ... мало, так что высшие гармонические составляющие практически не влияют
на форму выходного сигнала ![]() и
и
![]() ,
,
где ![]() –
амплитуда первой гармоники тока коллектора
–
амплитуда первой гармоники тока коллектора ![]() .
.
![]() – сопротивление
параллельного контура на резонансной частоте w .
– сопротивление
параллельного контура на резонансной частоте w .
Рис. 5.36Рис. 5.37
Выходное напряжение
![]()
практически оказывается косинусоидальным (т. е. гармоническим).
Вычислим КПД нелинейного резонансного
усилителя. Мощность, потребляемая от источника, ![]() .
Полезная активная мощность в колебательном контуре
.
Полезная активная мощность в колебательном контуре
![]() .
.
Отсюда
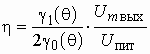 .
.
В мощных усилителях обычно стремятся
максимально использовать источник питания и получают ![]() ,
поэтому КПД
,
поэтому КПД
![]() .
.
Исследования показывают, что
с уменьшением q отношение ![]() растет,
т. е. КПД увеличивается, но одновременно падает амплитуда первой гармоники.
Считается, что оптимальным значением является q = 90° , при этом отношение
функций Берга равно 1,517. Это соответствует КПД около 76%.
растет,
т. е. КПД увеличивается, но одновременно падает амплитуда первой гармоники.
Считается, что оптимальным значением является q = 90° , при этом отношение
функций Берга равно 1,517. Это соответствует КПД около 76%.
Таким образом, нелинейный резонансный усилитель работает в более выгодном энергетическом режиме по сравнению с линейным усилителем.

Схема резонансного умножителя частоты отличается от нелинейного резонансного усилителя (см. рис. 5.36) только тем, что колебательный контур в выходной цепи настраивается на частоту одной из высших гармоник входного сигнала.
Амплитуда выходного сигнала умножителя при кусочно-линейной аппроксимации равна
![]() ,
,
а выходной сигнал
![]()
имеет частоту в k раз больше, чем у входного сигнала
![]() .
.
При больших k функции ![]() имеют небольшие значения, поэтому важно выбрать угол отсечки q , при котором
значение соответствующей функции Берга максимально. Существует оптимальный угол
отсечки
имеют небольшие значения, поэтому важно выбрать угол отсечки q , при котором
значение соответствующей функции Берга максимально. Существует оптимальный угол
отсечки ![]() , при
котором амплитуда выходного напряжения получается наибольшей.
, при
котором амплитуда выходного напряжения получается наибольшей.
Умножители частоты применяются в радиотехнике для получения высокочастотных стабильных колебаний, когда в распоряжении имеется стабильный низкочастотный генератор. Если отклонение частоты w , генерируемое низкочастотной схемой, составляет D w , то относительная нестабильность частоты равна D w /w . В умножителе частоты вместо частоты w + D w получаем частоту k(w + D w ), а относительная нестабильность kD w /kw остается такой же, как и у низкочастотного генератора.

К ограничителям мгновенных значений
предъявляются следующие требования. Если мгновенное значение входного сигнала
превышает заданное значение, называемое порогом ограничения, то значение выходного
сигнала должно оставаться неизменным. Различают ограничения снизу, сверху и
двухстороннее. Ограничение снизу наглядно демонстрирует рис. 5.33. Таким образом,
в схеме на транзисторе можно совмещать функции усилителя и ограничителя, если
амплитуда входного сигнала “выходит” за рамки линейного участка ВАХ (см. рис.
5.33), а в цепи коллектора включена резистивная нагрузка (см. рис. 5.35, а).
Порог ограничения можно регулировать напряжением смещения ![]() .
.
Ограничение сигнала сверху и двухстороннее
ограничение можно также осуществить на транзисторном резистивном каскаде (см.
рис. 5.35, а), если ВАХ ![]() будет иметь вид, показанный на рис. 5.37. Ограничение происходит за счет верхней
отсечки тока, двухстороннее ограничение – за счет нижней и верхней отсечки тока
будет иметь вид, показанный на рис. 5.37. Ограничение происходит за счет верхней
отсечки тока, двухстороннее ограничение – за счет нижней и верхней отсечки тока
![]() . Указанная характеристика
. Указанная характеристика
![]() транзистора получается
при использовании существенно пониженного напряжения коллекторного питания
транзистора получается
при использовании существенно пониженного напряжения коллекторного питания ![]() .
Идеализация характеристики достигается применением кусочно-линейной аппроксимации
тремя отрезками прямых.
.
Идеализация характеристики достигается применением кусочно-линейной аппроксимации
тремя отрезками прямых.
Ограничители мгновенных значений могут строиться на схемах с диодами, ВАХ которых могут быть также аппроксимированы отрезками прямых. На рис. 5.39 приведены схемы диодных ограничителей снизу (а), сверху (б) и двухстороннего (в). В этих схемах сигнал появляется на выходе, если диод закрыт. Меняя величину пороговых напряжений, можно осуществлять ограничение на разных уровнях. Для правильной работы схемы необходимо, чтобы сопротивление резистора R было во много раз больше дифференциального сопротивления диода в открытом состоянии.
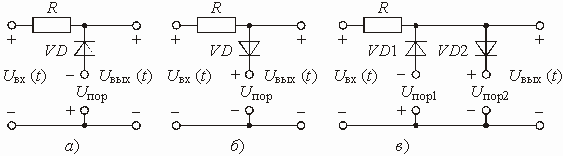
Рис. 5.39
Задача ограничителя амплитудных значений состоит в том, чтобы из сигнала с переменной амплитудой получить на его выходе колебание с постоянной амплитудой. Такая операция может быть выполнена с помощью нелинейного резонансного усилителя (см. рис. 5.36), работающего в режимах нижней и верхней отсечки тока. При этом будут получаться почти прямоугольные импульсы, подобные приведенным на рис. 5.37. Гармоническое же колебание с постоянной амплитудой выделяется колебательным контуром, настроенным на частоту сигнала w .
Ограничители мгновенных значений применяются, например, когда необходимо из синусоидального сигнала получить импульсы, близкие к прямоугольному. Ограничители амплитудных значений широко используются для устранения паразитных изменений амплитуды сигнала, которые могут возникнуть при передаче сигнала.

Подадим на вход цепи (рис. 5.40),
состоящей из последовательного соединения диода и резистора ![]() ,
гармоническое напряжение. Когда подаваемое на диод напряжение таково, что его
анод положителен по отношению к катоду, в цепи течет ток. Форма тока – синусоидальная
в течение первой половины периода. Когда полярность напряжения меняется на противоположную,
анод становится отрицательным по отношению к катоду, и тока в цепи нет.
,
гармоническое напряжение. Когда подаваемое на диод напряжение таково, что его
анод положителен по отношению к катоду, в цепи течет ток. Форма тока – синусоидальная
в течение первой половины периода. Когда полярность напряжения меняется на противоположную,
анод становится отрицательным по отношению к катоду, и тока в цепи нет.
Напряжение на резисторе ![]() пропорционально
току и поэтому представляет собой последовательность однополярных синусоидальных
импульсов. Этот процесс называется выпрямлением.
пропорционально
току и поэтому представляет собой последовательность однополярных синусоидальных
импульсов. Этот процесс называется выпрямлением.
Приложенное напряжение изменяется по закону синуса; в первом полупериоде диод работает в режиме прямого смещения, а в следующем полупериоде – в режиме обратного смещения (см. рис. 5.29). Только при прямом смещении диода через него протекает ток. Падением напряжения на диоде в этот период времени пренебрегают.
Поскольку выпрямитель проводит ток только в течение одной половины периода приложенного напряжения, то и называется он полуволновым выпрямителем.
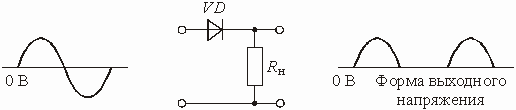
Рис. 5.40
Очевидно, что в выпрямителе, изображенном на рис. 5.40, выходное напряжение не является постоянным, как это требуется в цепях питания для электронной аппаратуры.
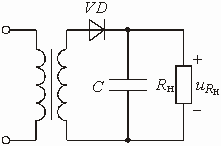
Рис. 5.41
Исследование формы сигнала показывает
наличие пульсаций напряжения. Для того, чтобы сгладить эти пульсации и получить
напряжение питания требуемого постоянного уровня, параллельно сопротивлению
![]() подключают емкость
С (рис. 5.41), т. е. используют схему простейшего фильтра. Значение емкости
должно быть большим (500 ё 5000 мкФ). Выпрямленные импульсы заряжают емкость
до напряжения близкого к максимальному значению, создаваемому выпрямителем (рис. 5.42).
Из-за больших значений емкости С постоянная времени
подключают емкость
С (рис. 5.41), т. е. используют схему простейшего фильтра. Значение емкости
должно быть большим (500 ё 5000 мкФ). Выпрямленные импульсы заряжают емкость
до напряжения близкого к максимальному значению, создаваемому выпрямителем (рис. 5.42).
Из-за больших значений емкости С постоянная времени ![]() будет
тоже большой по сравнению с периодом приложенного напряжения.
будет
тоже большой по сравнению с периодом приложенного напряжения.
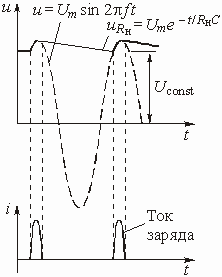
Рис. 5.42
Напряжение на сопротивлении поэтому уменьшается не по закону синуса, а по экспоненциальному закону в соответствии с уравнением
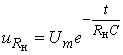 .
.
Падение напряжения может быть уменьшено для данной нагрузки увеличением значения С.
Напряжение на выходе выпрямителя,
когда используется один конденсатор, не является гладким, но может рассматриваться
в виде малых пульсаций напряжения, наложенных на сравнительно большое постоянное
напряжение ![]() . Это
постоянное напряжение и является требуемым напряжением, а переменное пульсирующее
напряжение должно быть устранено.
. Это
постоянное напряжение и является требуемым напряжением, а переменное пульсирующее
напряжение должно быть устранено.
Чтобы уменьшить пульсации до приемлемого уровня, необходимо использовать селективный фильтр, который будет подавлять пульсирующее напряжение, но не будет значительно ослаблять постоянную составляющую. Схема такого фильтра приведена на рис. 5.43. Емкость представляет очень малое сопротивление переменным составляющим и очень большое сопротивление постоянной составляющей напряжения. Обычно используется емкость в несколько тысяч микрофарад. Амплитудно-частотная характеристика фильтра показана на рис. 5.44.
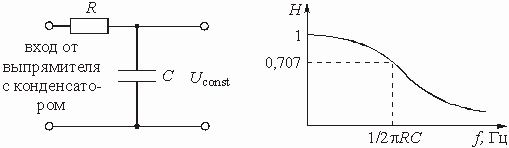
Рис. 5.43 Рис. 5.44
Схема двухполупериодного выпрямителя
приведена рис. 5.45, а, график выпрямленного напряжения ![]() –
на рис. 5.45, б.
–
на рис. 5.45, б.
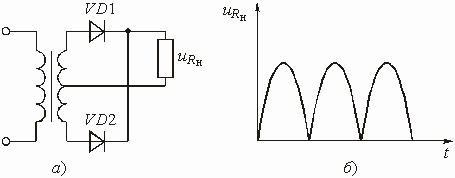
Рис. 5.45
Схема мостового выпрямителя с фильтром изображена на рис. 5.46.
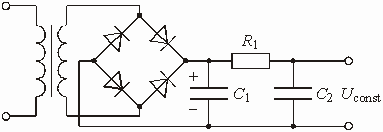
Рис. 5.46

Сигнал, состоящий из суммы двух
гармонических колебаний с различными частотами ![]() и
и
![]() и амплитудами
и амплитудами
![]() и
и ![]()
![]()
называется бигармоническим воздействием. Спектр бигармонического воздействия изображен на рис. 5.47, а.
Рис. 5.47
Пусть на вход НЭ, ВАХ которого аппроксимирована полиномом второй степени
![]() ,
,
подано напряжение смещения ![]() и
бигармонический сигнал
и
бигармонический сигнал ![]() . Подстановка
напряжения
. Подстановка
напряжения ![]() в выражение для ВАХ
позволяет определить ток в цепи НЭ в виде
в выражение для ВАХ
позволяет определить ток в цепи НЭ в виде
Используя тригонометрические формулы
![]()
и
![]() ,
,
получим
 (5.25)
(5.25)
Спектральный состав тока в цепи с НЭ показан на рис. 5.47, б.
Таблица 5.3
|
Значения q |
Частоты спектральных составляющих при значениях p |
|||
|
0 |
1 |
2 |
3 |
|
|
0 |
w = 0 |
|
|
|
|
1 |
|
|
|
– |
|
2 |
|
|
– |
– |
|
3 |
|
– |
– |
– |
Принципиально новым по сравнению
с воздействием на НЭ одного гармонического колебания здесь является появление
спектральных составляющих с комбинационными частотами ![]() и
и
![]() . Если ВАХ нелинейного
элемента аппроксимирована в общем случае полиномом степени N, то в спектральном
составе тока будут присутствовать составляющие с комбинационными частотами
. Если ВАХ нелинейного
элемента аппроксимирована в общем случае полиномом степени N, то в спектральном
составе тока будут присутствовать составляющие с комбинационными частотами ![]() ,
причем
,
причем ![]() , где p
и q – целые положительные числа (0, 1, 2, ...). Так, например, при аппроксимации
ВАХ нелинейного элемента полиномом третьей степени в составе спектра тока присутствуют
комбинационные частоты, приведенные в табл. 5.3.
, где p
и q – целые положительные числа (0, 1, 2, ...). Так, например, при аппроксимации
ВАХ нелинейного элемента полиномом третьей степени в составе спектра тока присутствуют
комбинационные частоты, приведенные в табл. 5.3.
В общем случае входное воздействие можно представить бесконечной суммой
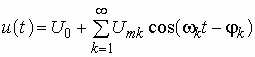 .
.
В зависимости от степени N аппроксимирующего полинома (5.13) в спектре тока, протекающего через нелинейный элемент, появляются комбинационные частоты вида:
![]()
p, q, s, k
– целые положительные числа. Например, при воздействии на НЭ с ВАХ в виде полинома
второй степени суммы трех гармонических колебаний в спектре тока, помимо постоянной
составляющей и первых двух гармоник каждой частоты, присутствуют комбинационные
частоты ![]() ;
; ![]() ;
;
![]() . При аппроксимации
полиномом третьей степени дополнительно появляются третьи гармоники
. При аппроксимации
полиномом третьей степени дополнительно появляются третьи гармоники ![]() ,
,
![]() ,
, ![]() и
комбинационные частоты типа
и
комбинационные частоты типа ![]() ;
;
![]() ;
; ![]() и
т. д.
и
т. д.

При передаче электрических сигналов на расстояние часто требуется переносить спектр сигнала вверх или вниз по шкале частот. Такой перенос спектра называется преобразованием частоты. Необходимость в преобразовании частот возникает, например, в случаях если спектр сигнала, который можно передать, расположен на шкале частот значительно ниже полосы пропускания системы передачи.
В качестве преобразователя частоты может быть использован усилительный каскад на транзисторе с колебательным контуром (рис. 5.48). Предположим, что нужно перенести вверх по шкале частот на значение w гармоническое низкочастотное колебание с частотой W :
![]() .
.
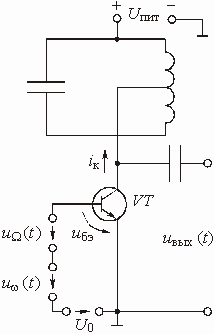
Рис. 5.48
Подадим на вход нелинейного резонансного усилителя, кроме этого колебания, также высокочастотное колебание с частотой w :
![]() .
.
Амплитуды напряжений смещения ![]() ,
низкочастотного
,
низкочастотного ![]() и
высокочастотного
и
высокочастотного ![]() колебаний
выберем так, чтобы работать на участке ВАХ, который достаточно точно аппроксимируется
полиномом второй степени
колебаний
выберем так, чтобы работать на участке ВАХ, который достаточно точно аппроксимируется
полиномом второй степени
![]() . (5.26)
. (5.26)
Напряжение на участке база – эмиттер
![]() .
.
После подстановки этого выражения в зависимость (5.26) в формуле для тока появляются в соответствии с (5.25) гармонические колебания с частотами W , w , 2W , 2w и с суммарной и разностной комбинационными частотами w + W и w – W .
Колебательный контур резонансного усилителя настроен на частоту w + W и выделяет из спектрального состава тока колебание
![]() .
.
Выделенное колебание тока создает
на резонансном сопротивлении контура ![]() падение
напряжения
падение
напряжения
![]() ,
,
которое и является выходным сигналом преобразователя частоты.
В реальных системах связи передаваемый
низкочастотный сигнал не является гармоническим, а имеет сложный спектр ![]() (рис.
5.49, а), т. е. состоит из суммы гармонических колебаний с частотами
(рис.
5.49, а), т. е. состоит из суммы гармонических колебаний с частотами
![]() ,
, ![]() ,
,
![]() , ... .
, ... .
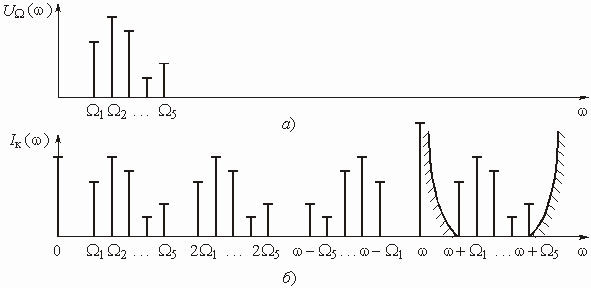
Рис. 5.49
Если этот сигнал вместе с высокочастотным
колебанием ![]() подать
на нелинейный элемент, то в спектре тока
подать
на нелинейный элемент, то в спектре тока ![]() (рис.
5.49, б), протекающего через НЭ, будут присутствовать полезные продукты
преобразования – комбинационные частоты
(рис.
5.49, б), протекающего через НЭ, будут присутствовать полезные продукты
преобразования – комбинационные частоты ![]() ,
,
![]() ,
, ![]() ,
... . Чтобы отфильтровать токи с этими частотами, недостаточно воспользоваться
одиночным колебательным контуром, поскольку он не сможет обеспечить хорошую
фильтрацию полезных продуктов преобразования. Его можно заменить в схеме рис.
5.48 обычной резистивной нагрузкой, а на выходе схемы включить электрический
фильтр с характеристикой ослабления (на рис. 5.49, б она показана штриховой
линией), обеспечивающей необходимую степень подавления несущего колебания с
частотой w .
,
... . Чтобы отфильтровать токи с этими частотами, недостаточно воспользоваться
одиночным колебательным контуром, поскольку он не сможет обеспечить хорошую
фильтрацию полезных продуктов преобразования. Его можно заменить в схеме рис.
5.48 обычной резистивной нагрузкой, а на выходе схемы включить электрический
фильтр с характеристикой ослабления (на рис. 5.49, б она показана штриховой
линией), обеспечивающей необходимую степень подавления несущего колебания с
частотой w .
Приведем еще несколько практических схем преобразователей частоты. На рис. 5.50 представлены диодные преобразователи: однотактный (а), двухтактный или балансный (б) и кольцевой (в), работающие в режиме больших амплитуд колебания частоты w , т. е. в режиме аппроксимации ВАХ диодов линейно-ломаными функциями. Схема балансного транзисторного преобразователя частоты показана на рис. 5.51.
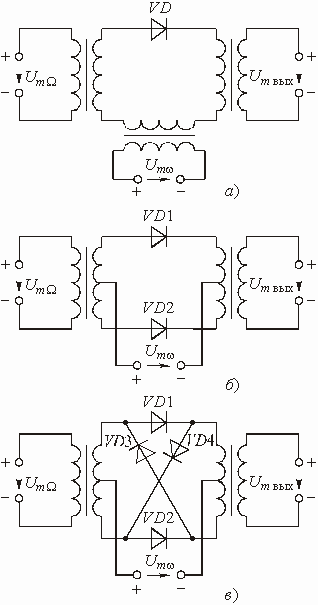
Рис. 5.50
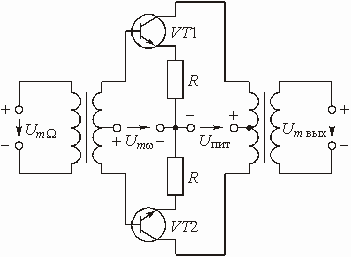
Рис. 5.51
В балансных и кольцевых преобразователях гораздо меньше побочных продуктов преобразования; тем самым значительно облегчаются требования к фильтру, выделяющему полезные колебания.
Примеры к главе 5
Пример 5.1
Рассчитать ток, протекающий через
нелинейный элемент в цепи, изображенной на рис. 5.7 Заданы: ВАХ НЭ ![]() (рис.
5.8),
(рис.
5.8), ![]() = 2 кОм,
U = 1 В,
= 2 кОм,
U = 1 В, ![]() =
= 0,5 мА.
=
= 0,5 мА.
Для построения прямой (5.3) рассчитаем напряжение холостого хода между узлами 1 и 2 (при отключении НЭ), эквивалентное сопротивление пассивного двухполюсника и ток короткого замыкания (при закороченном НЭ):
![]() 2
В;
2
В;
![]() 2
кОм;
2
кОм;
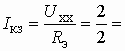 1
мА.
1
мА.
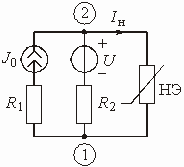
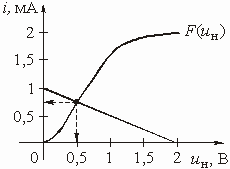
Рис. 5.7 Рис. 5.8
Строим график прямой (5.2) по аналогии
с графиком, изображенным на рис. 5.6. Точка пересечения этой прямой с ВАХ НЭ
(рис. 5.8) дает значения тока ![]() 0,7
мА, протекающего через НЭ, и напряжения
0,7
мА, протекающего через НЭ, и напряжения ![]() =
0,5 В на нем.
=
0,5 В на нем.
Пример 5.2
Рассчитать напряжения и токи в цепи, схема которой изображена на рис. 5.13, где U = 5 В, R = 500 Ом, а ВАХ НЭ заданы графиками на рис. 5.14.
Поскольку ВАХ заданы графиками,
то при решении воспользуемся графическими построениями. Найдем ВАХ ![]() двухполюсника,
эквивалентного параллельному соединению линейного сопротивления R и НЭ2.
Для этого перенесем ВАХ НЭ2 на новый рисунок и построим ВАХ линейного
элемента (рис. 5.15, а). На этом же рисунке показана эквивалентная ВАХ
двухполюсника,
эквивалентного параллельному соединению линейного сопротивления R и НЭ2.
Для этого перенесем ВАХ НЭ2 на новый рисунок и построим ВАХ линейного
элемента (рис. 5.15, а). На этом же рисунке показана эквивалентная ВАХ
![]() . Перенесем эту
эквивалентную ВАХ и ВАХ НЭ1 на рис. 5.15, б и найдем ВАХ эквивалентного
двухполюсника
. Перенесем эту
эквивалентную ВАХ и ВАХ НЭ1 на рис. 5.15, б и найдем ВАХ эквивалентного
двухполюсника ![]() ,
который присоединяется к зажимам источника.
,
который присоединяется к зажимам источника.
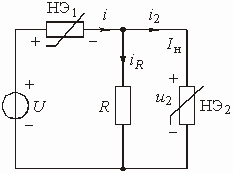
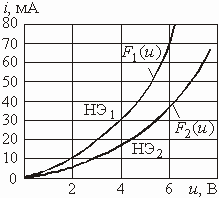
Рис. 5.13 Рис. 5.14
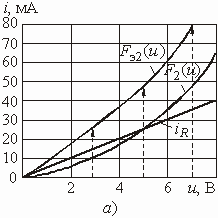
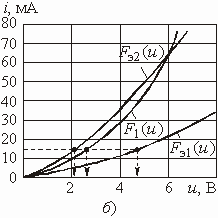
Рис. 5.15
По рис. 5.15, б по кривой
![]() находим, что напряжению
u = 5 В соответствует ток i = 16 мА, по кривой
находим, что напряжению
u = 5 В соответствует ток i = 16 мА, по кривой ![]() –
напряжение на НЭ1
–
напряжение на НЭ1 ![]() =
2,8 В и по кривой
=
2,8 В и по кривой ![]() –
напряжение на параллельном соединении R и НЭ2
–
напряжение на параллельном соединении R и НЭ2 ![]() =
2,2 В. Зная это напряжение, по графикам рис. 5.15, a находим
=
2,2 В. Зная это напряжение, по графикам рис. 5.15, a находим ![]() =
11 мА и
=
11 мА и ![]() = 5 мА.
= 5 мА.
Пример 5.3
На рис. 5.16, а показана
подключенная к источнику напряжения цепь из трех резистивных НЭ. Суммирование
ординат характеристик элементов 2 и 3, соединенных параллельно, дает эквивалентную
характеристику 2 – 3 (рис. 5.16, б). Суммируя абсциссы последней с абсциссами
кривой 1, получаем эквивалентную характеристику нелинейной цепи ![]() .
Из графиков рис. 5.16, б можно, задаваясь напряжением на входе, получить
токи и напряжения ветвей.
.
Из графиков рис. 5.16, б можно, задаваясь напряжением на входе, получить
токи и напряжения ветвей.
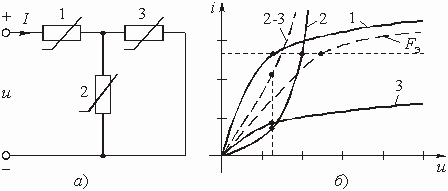
Рис. 5.16
Пример 5.4
Рассчитать ток ![]() и
напряжение
и
напряжение ![]() на
нелинейном элементе, а также ток
на
нелинейном элементе, а также ток ![]() в
цепи, изображенной на рис. 5.17, если заданы значения
в
цепи, изображенной на рис. 5.17, если заданы значения ![]() =
1 кОм,
=
1 кОм, ![]() = 14 В,
= 14 В,
![]() = = 10 мА,
= = 10 мА,
![]() А/В.
А/В.
Предположим вначале, что решение
системы уравнений (5.5), (5.6), (5.4) существует при ![]() .
Тогда уравнение НЭ имеет вид
.
Тогда уравнение НЭ имеет вид
![]() . (5.7)
. (5.7)
Выразим из уравнения (5.5) ток
![]() и подставим его
в уравнение (5.6). В результате этой операции получим
и подставим его
в уравнение (5.6). В результате этой операции получим
![]() . (5.8)
. (5.8)
Подставив в (5.8) выражение (5.7), получим уравнение относительно неизвестного напряжения на нелинейном двухполюснике
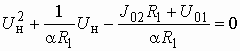 . (5.9)
. (5.9)
Отсюда имеем
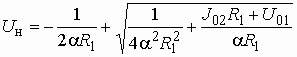 . (5.10)
. (5.10)
Подставляя в (5.10) заданные значения
![]() ,
, ![]() ,
,
![]() и
и ![]() ,
получаем
,
получаем ![]() = 20
В.
= 20
В.
Второе решение уравнения (5.9)
даст ![]() . Это решение
не подходит, так как применялось уравнение НЭ, справедливое при
. Это решение
не подходит, так как применялось уравнение НЭ, справедливое при ![]() .
.
Допустим теперь существование решения
системы уравнений (5.5) – (5.6) при ![]() .
Согласно уравнению НЭ (5.4)
.
Согласно уравнению НЭ (5.4) ![]() .
Тогда из уравнения (5.8) имеем
.
Тогда из уравнения (5.8) имеем
![]() 24
В > 0,
24
В > 0,
а это противоречит условию, что
![]() .
.
Таким образом, остается первое
решение (5.10). Найдем остальные неизвестные. Из (5.7) имеем ![]() =
=
![]() мА, а из (5.5)
мА, а из (5.5)
![]() –6 мА.
–6 мА.
В данном примере получено аналитическое решение системы нелинейных уравнений. Если бы ВАХ нелинейного элемента описывалась более сложной функцией, то этого достичь не удалось бы.
Пример 5.5
Аппроксимировать экспериментальную
зависимость тока базы ![]() от
напряжения между базой и эмиттером
от
напряжения между базой и эмиттером ![]() для
биполярного транзистора, заданную в таблице 5.1.
для
биполярного транзистора, заданную в таблице 5.1.
Таблица 5.1
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
|
0,05 |
0,07 |
0,1 |
0,175 |
0,3 |
0,53 |
Известно также, что напряжение
смещения ![]() и что
амплитуда гармонического напряжения на входе транзистора не превышает 0,2 В,
т. е.
и что
амплитуда гармонического напряжения на входе транзистора не превышает 0,2 В,
т. е. ![]() Ф 0,2 В.
Ф 0,2 В.
Экспериментальные точки из табл. 5.1 показаны на графике рис. 5.22 кружочками, соединенными пунктиром.
Можно потребовать, чтобы значения
степенного полинома совпадали со значениями тока ![]() для
всех шести значений напряжения
для
всех шести значений напряжения ![]() ,
указанных в таблице. В этом случае необходимо выбрать степенной полином 5-ой
степени (т.к. он содержит 6 коэффициентов).
,
указанных в таблице. В этом случае необходимо выбрать степенной полином 5-ой
степени (т.к. он содержит 6 коэффициентов).
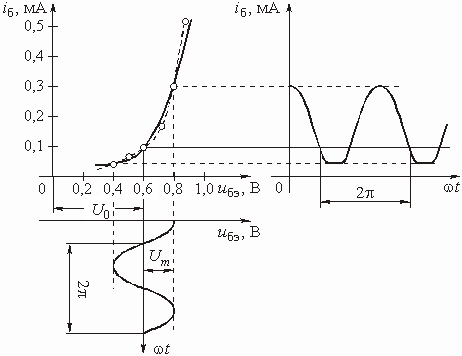
Рис. 5.22
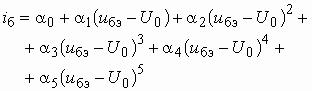 (5.14)
(5.14)
и составить систему уравнений.
Первое уравнение получаем, подставляя в (5.14) значения ![]() и
и
![]() :
:
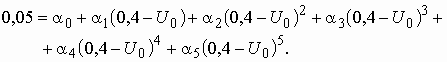
Второе уравнение получаем, подставляя
в (5.14) значения ![]() и
и
![]() :
:
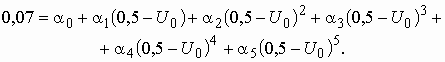
Третье уравнение получаем, подставляя
в (5.14) значения ![]() и
и
![]() :
:
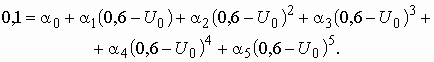
Четвертое уравнение получаем, подставляя
в (5.14) значения ![]() и
и
![]() :
:
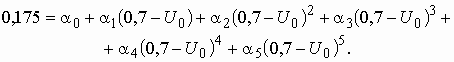
Пятое уравнение получаем, подставляя
в (5.14) значения ![]() и
и
![]() :
:
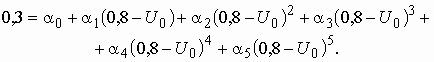
И, наконец, шестое уравнение получаем,
подставляя в (5.14) значения ![]() и
и
![]() :
:
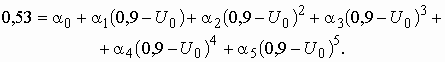
Учитывая, что ![]() ,
получим окончательно следующую систему:
,
получим окончательно следующую систему:
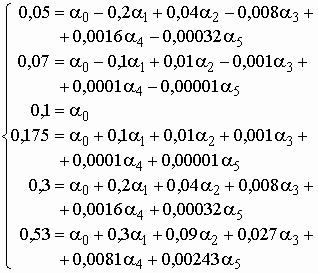 (5.15)
(5.15)
Решение системы уравнений (5.15)
даст искомые значения коэффициентов ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() и
и
![]() , при которых
ток базы
, при которых
ток базы ![]() (5.14)
будет совпадать во всех узлах интерполяции со значениями тока из Табл. 5.1.
По формуле (5.14) можно вычислить любые промежуточные значения тока и построить
точный график аппроксимирующей функции.
(5.14)
будет совпадать во всех узлах интерполяции со значениями тока из Табл. 5.1.
По формуле (5.14) можно вычислить любые промежуточные значения тока и построить
точный график аппроксимирующей функции.
Заметим, что решение системы уравнений, состоящей из 6-ти уравнений с 6-ю неизвестными, в настоящее время не представляет заметных трудностей. Для этих целей существуют программы не только для персональных компьютеров, но и для микрокалькуляторов.
Однако, нет необходимости аппроксимировать
ВАХ вне интервала 0,4 В Ф ![]() Ф
0,8 В, так как мы знаем, что сигнал на входе транзистора не выходит за эти пределы
(действительно,
Ф
0,8 В, так как мы знаем, что сигнал на входе транзистора не выходит за эти пределы
(действительно, ![]() и
и
![]() ). Кроме того,
можно выбрать меньше узлов интерполяции (например,
). Кроме того,
можно выбрать меньше узлов интерполяции (например, ![]() ;
0,6 В; 0,8 В), что позволит уменьшить степень аппроксимирующего полинома
до 2-ой:
;
0,6 В; 0,8 В), что позволит уменьшить степень аппроксимирующего полинома
до 2-ой:
![]() .
.
Система уравнений будет состоять всего из 3-х уравнений и содержать 3 неизвестных:
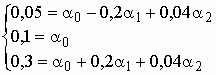
Решение этой системы дает ![]() ,
,
![]() 0,625 мА/В,
0,625 мА/В, ![]() .
Кривая тока
.
Кривая тока
![]() (5.16)
(5.16)
Таблица 5.2
|
|
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
Значения |
0,05 |
0,05625 |
0,1 |
0,18125 |
0,3 |
0,45625 |
проходит через три экспериментальные точки (рис. 5.22).
В табл. 5.2 приведены для сравнения
значения тока базы ![]() вычисленные
из (5.16). Из рисунка и таблиц видно, что экспериментальные точки достаточно
плотно “ ложатся” на кривую (5.16).
вычисленные
из (5.16). Из рисунка и таблиц видно, что экспериментальные точки достаточно
плотно “ ложатся” на кривую (5.16).
Пример 5.6
Аппроксимировать график ![]() зависимости
тока стока от напряжения между затвором и истоком для полевого транзистора (рис.
5.24), на вход которого подается напряжение
зависимости
тока стока от напряжения между затвором и истоком для полевого транзистора (рис.
5.24), на вход которого подается напряжение ![]() ,
В.
,
В.
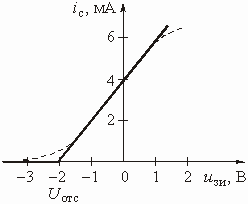
Рис. 5.24
Транзистор работает в режиме большого
сигнала, поэтому его ВАХ аппроксимируется двумя прямыми линиями. По графику
![]() находим напряжение
отсечки
находим напряжение
отсечки ![]() = –2 В.
По аналогии с (5.17) в диапазоне изменения напряжения
= –2 В.
По аналогии с (5.17) в диапазоне изменения напряжения ![]() Ф
–2 В ток стока
Ф
–2 В ток стока ![]() равен
нулю. Когда напряжение
равен
нулю. Когда напряжение ![]() становится
больше
становится
больше ![]() , то крутизна
S аппроксимирующей прямой рассчитывается по формуле
, то крутизна
S аппроксимирующей прямой рассчитывается по формуле
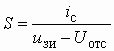 .
.
Подставляя в эту формулу значения
![]() и
и ![]() на
границе рабочего диапазона, т. е.
на
границе рабочего диапазона, т. е. ![]() =
0,
=
0, ![]() = 4 мА, получаем
S = 2 мА/В.
= 4 мА, получаем
S = 2 мА/В.
Таким образом, аппроксимирующая ВАХ функция имеет вид
![]()
или
![]()
Пример 5.7
Рассчитать спектральный состав тока базы биполярного транзистора для данных Примера 5.5. Построить спектр тока.
В рабочем диапазоне напряжений
0,4 В Ф ![]() Ф 0,8
В ВАХ транзистора была аппроксимирована полиномом
Ф 0,8
В ВАХ транзистора была аппроксимирована полиномом
2-ой степени (5.20)
![]() .
.
Коэффициенты полинома были определены в Примере 5.5 (см. формулу (5.16)):
![]() =
0,1 мА;
=
0,1 мА; ![]() = 0,625
мА/В;
= 0,625
мА/В; ![]() = 1,875
мА/В2.
= 1,875
мА/В2.
Рассчитаем значения постоянной составляющей и амплитуды первой и второй гармоник тока, воспользовавшись вышеприведенными формулами:
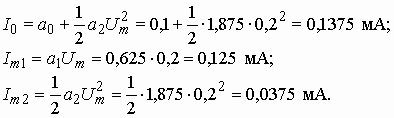
Спектр тока (рис. 5.32) содержит
постоянную составляющую ![]() и
две гармоники с амплитудами
и
две гармоники с амплитудами ![]() и
и
![]() .
.
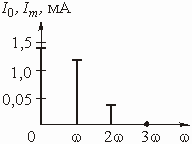
Рис. 5.32
Пример 5.8
Рассчитать постоянную составляющую и амплитуды первой и второй гармоник в спектре тока стока полевого транзистора для данных Примера 5.6.
По данным Примера 5.6 напряжение
смещения ![]() = –3
В, амплитуда гармонического напряжения
= –3
В, амплитуда гармонического напряжения ![]() =
3 В, напряжение отсечки
=
3 В, напряжение отсечки ![]() =
–2 В, крутизна S = 2 мА/В.
=
–2 В, крутизна S = 2 мА/В.
По формуле (5.22) рассчитываем угол отсечки:
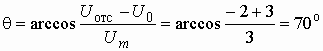 .
.
Для угла отсечки ![]() определяем
по графикам, приведенным на рис. 5.34, функции Берга:
определяем
по графикам, приведенным на рис. 5.34, функции Берга:
![]() ,
,
![]() .
.
Постоянную составляющую и амплитуды гармоник тока рассчитываем, используя формулу (5.23):
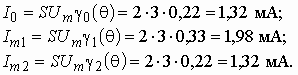
Амплитуды других гармоник в спектре тока можно рассчитать аналогично, выбрав в справочнике соответствующие функции Берга.
Пример 5.9
Рассчитать коэффициент гармоник усилителя на биполярном транзисторе, спектр тока базы которого был рассчитан в Примере 5.7.
ВАХ транзистора была аппроксимирована
полиномом 2-ой степени, поэтому в спектре тока есть только постоянная составляющая
![]() = 0,1375 мА и
две гармоники, имеющие амплитуды
= 0,1375 мА и
две гармоники, имеющие амплитуды ![]() =
0,125 мА и
=
0,125 мА и ![]() = 0,0375
мА. Коэффициент гармоник рассчитаем, воспользовавшись формулой (5.24):
= 0,0375
мА. Коэффициент гармоник рассчитаем, воспользовавшись формулой (5.24):
![]() .
.
Пример 5.10
Рассчитать КПД резонансного усилителя, если угол отсечки q = 70° (см. Пример 5.8).
В Примере 5.8 по графикам рис. 5.34 были определены значения функций Берга:
![]()
КПД нелинейного резонансного усилителя
![]() .
.
Пример 5.11
На вход усилителя (рис. 5.35, а)
поступает напряжение ![]() .
Проходная ВАХ
.
Проходная ВАХ ![]() транзистора
изображена на рис. 5.38 пунктиром. Построить график тока
транзистора
изображена на рис. 5.38 пунктиром. Построить график тока ![]() .
.
Аппроксимируем ВАХ транзистора
тремя отрезками прямых. Усилитель работает в режиме двухстороннего ограничения
тока. График тока ![]() построен,
используя метод проекций, и приведен на рис. 5.38.
построен,
используя метод проекций, и приведен на рис. 5.38.
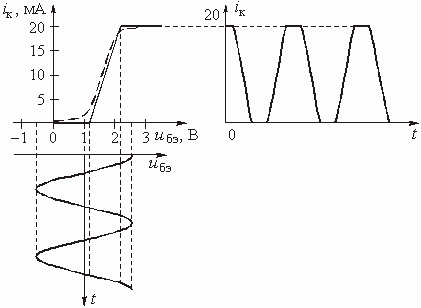
Рис. 5.38
Вопросы и задания для самопроверки
1. Какие резистивные элементы называются нелинейными?
2. Определить статическое и динамическое сопротивления нелинейного элемента, имеющего ВАХ, изображенную на рис. 5.22.
Ответ:
![]() =
6 кОм;
=
6 кОм; ![]() =
1,9 кОм.
=
1,9 кОм.
3. Какие методы используют для расчета нелинейных цепей в режиме постоянного тока?
4. Рассчитать ток, протекающий
через нелинейный элемент в схеме рис. 5.52, а, если заданы ![]() =
2 кОм,
=
2 кОм, ![]() =
2 В,
=
2 В, ![]() =
8 В, ВАХ НЭ приведена на рис. 5.52, б.
=
8 В, ВАХ НЭ приведена на рис. 5.52, б.
Ответ:
![]() =
2,7 мА.
=
2,7 мА.
5. Рассчитать ток I в схеме рис. 5.53, а, если R = 0,5 кОм, E = 2 В, ВАХ НЭ1 и НЭ2 приведены на рис. 5.53, б.
Ответ: I = 2,25 мА.
6. Каким образом формируются уравнения состояния нелинейных резистивных цепей?
7. Каков порядок расчета резистивных цепей с нелинейными четырехполюсниками?
8. Какие существуют виды аппроксимации ВАХ нелинейных элементов?
9. Аппроксимировать ВАХ НЭ,
изображенную на рис. 5.8, в рабочем диапазоне 0 Ô
![]() Ô
1 В при
Ô
1 В при ![]() =
0,5 В.
=
0,5 В.
Ответ:
![]() .
.
10. Аппроксимировать ВАХ
НЭ, изображенную на рис. 5.8, если к НЭ приложено напряжение ![]() .
.
Ответ:
![]()
|
Рис. 5.52 Рис. 5.53 |
11. Рассчитать амплитуды спектральных составляющих тока в задаче 9. Построить спектр тока.
Ответ:
![]() =
0,725 мА;
=
0,725 мА; ![]() =
0,75 мА;
=
0,75 мА; ![]() =
0,025 мА.
=
0,025 мА.
12. Рассчитать постоянную
составляющую и амплитуды спектральных составляющих ![]() и
и
![]() тока
в задаче 10. Построить спектр тока.
тока
в задаче 10. Построить спектр тока.
Ответ:
q
= 75,5°; ![]() =
0,6 мА;
=
0,6 мА; ![]() =
0,9 мА;
=
0,9 мА; ![]() =
0,5 мА.
=
0,5 мА.
13. Построить графики тока
![]() биполярного
транзистора, ВАХ которого изображена на рис. 5.23, если заданы следующие значения
биполярного
транзистора, ВАХ которого изображена на рис. 5.23, если заданы следующие значения
![]() :
:
а)
![]() ;
;
б)
![]() ;
;
б)
![]() .
.
14. По графикам рис. 5.35 и 5.37 пояснить принцип работы резистивного и резонансного нелинейных усилителей. Сравнить их КПД.
15. На вход резонансного усилителя (рис. 5.36) поступает гармоническое колебание частотой 50 кГц. Как получить на выходе напряжение частотой 150 кГц? Каким должен быть при этом угол отсечки и как добиться оптимального значения q?
16. Построить качественно
графики напряжений ![]() в
схемах ограничителей рис. 5.39, а
– в.
в
схемах ограничителей рис. 5.39, а
– в.
17. По графику рис. 5.42 пояснить принцип работы выпрямителя, схема которого изображена на рис. 5.41.
18. Как сгладить пульсации напряжения на выходе выпрямителя?
19. Какой спектр имеет бигармоническое воздействие? Каков спектральный состав тока в цепи с НЭ, на который подано бигармоническое воздействие?
20. Какие комбинационные частоты будут в спектре НЭ, если его ВАХ аппроксимирована полиномом четвертой степени?
21. Каким образом можно перенести спектр сигнала по шкале частот?
Глава 6. Генераторы

Автогенераторы (или, чаще, генераторы) используются в радиотехнике и связи для получения электромагнитных колебаний. В зависимости от формы колебаний различают генераторы гармонических и негармонических (прямоугольных, пилообразных, импульсных и т. п.) колебаний.
В качестве активных элементов в генераторах применяются электронные лампы, биполярные и полевые транзисторы и др. Различие в элементной базе пассивной части схемы генератора позволяет вести речь о LC–генераторах или о RC–генераторах.
На рис. 6.1, а показан параллельный колебательный контур, состоящий из элементов L, C и G. Если контуру сообщить некоторое количество энергии, то в нем возникнут свободные гармонические колебания. Из-за наличия резистивной проводимости G в контуре имеются потери и колебания будут затухающими, т. е. напряжение на контуре будет иметь вид затухающей синусоиды (рис. 6.1, б):
![]() ,
,
где ![]() – начальная амплитуда напряжения на контуре,
a– коэффициент затухания
контура;
– начальная амплитуда напряжения на контуре,
a– коэффициент затухания
контура; ![]() –
частота свободных колебаний;
–
частота свободных колебаний; ![]() – резонансная частота контура; j
– начальная фаза колебания.
– резонансная частота контура; j
– начальная фаза колебания.
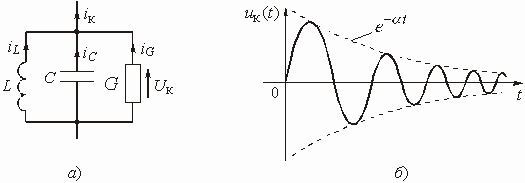
Рис. 6.1
Чтобы превратить такой контур в
генератор незатухающих гармонических колебаний, нужно возмещать в нем потери,
т. е. пополнять контур энергией. Энергию в контуре можно пополнять, например,
за счет собственных колебаний, снятых с контура и усиленных усилителем. Работающая
на таком принципе схема автогенератора показана на рис. 6.2 (источник питания
обозначен на схеме ![]() ).
Она состоит из биполярного транзистора, в коллекторную цепь которого включен
колебательный контур. С помощью трансформатора напряжение снимается с контура
и подается на вход (участок « база – эмиттер» ) транзистора.
).
Она состоит из биполярного транзистора, в коллекторную цепь которого включен
колебательный контур. С помощью трансформатора напряжение снимается с контура
и подается на вход (участок « база – эмиттер» ) транзистора.
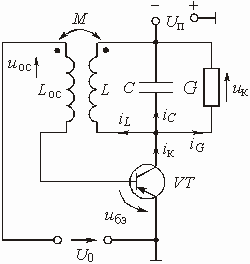
Рис. 6.2
Причиной возникновения колебаний
в автогенераторе являются флуктуации тока в элементах реальной схемы (за счет
теплового движения электронов в активных элементах и резисторах, дробового эффекта
в активных элементах и т. д.), а также за счет внешних помех. Флуктуации тока
![]() , протекающего
через контур, вызывают флуктуации напряжения на контуре
, протекающего
через контур, вызывают флуктуации напряжения на контуре ![]() .
Спектр этих случайных флуктуаций весьма широк и содержит составляющие всех частот.
.
Спектр этих случайных флуктуаций весьма широк и содержит составляющие всех частот.
Составляющие напряжения ![]() с частотами, близкими к резонансной частоте контура
с частотами, близкими к резонансной частоте контура ![]() ,
будут иметь наибольшую амплитуду, так как модуль комплексного эквивалентного
сопротивления контура является наибольшим и равным
,
будут иметь наибольшую амплитуду, так как модуль комплексного эквивалентного
сопротивления контура является наибольшим и равным ![]() именно на этой частоте
именно на этой частоте ![]() .
Выделенное на контуре синусоидальное с частотой
.
Выделенное на контуре синусоидальное с частотой ![]() напряжение через цепь обратной связи, образованную трансформатором, передается
на вход транзистора, создавая напряжение
напряжение через цепь обратной связи, образованную трансформатором, передается
на вход транзистора, создавая напряжение ![]() .
Это напряжение вызовет увеличение коллекторного тока
.
Это напряжение вызовет увеличение коллекторного тока ![]() ,
что, в свою очередь, приведет к увеличению напряжения на контуре
,
что, в свою очередь, приведет к увеличению напряжения на контуре ![]() .
Как следствие этого увеличатся напряжение обратной связи
.
Как следствие этого увеличатся напряжение обратной связи ![]() и напряжение
и напряжение ![]() и, значит, вновь увеличатся коллекторный ток и напряжение на контуре
и, значит, вновь увеличатся коллекторный ток и напряжение на контуре ![]() и т. д. Таким образом, в замкнутой системе автогенератора самовозбуждаются колебания
частоты, близкой к резонансной частоте контура
и т. д. Таким образом, в замкнутой системе автогенератора самовозбуждаются колебания
частоты, близкой к резонансной частоте контура ![]() .
.
Очевидно, важным условием возникновения
колебаний является то, что фаза напряжения ![]() должна быть такой, чтобы увеличение напряжения
должна быть такой, чтобы увеличение напряжения ![]() вызывало увеличение коллекторного тока
вызывало увеличение коллекторного тока ![]() и, тем самым, новое увеличение
и, тем самым, новое увеличение ![]() .
Это условие и есть условие баланса фаз. Баланс фаз достигается правильным включением
вторичной обмотки трансформатора. При переполюсовке обмотки трансформатора возрастание
напряжения на контуре
.
Это условие и есть условие баланса фаз. Баланс фаз достигается правильным включением
вторичной обмотки трансформатора. При переполюсовке обмотки трансформатора возрастание
напряжения на контуре ![]() приведет
к уменьшению коллекторного тока, т. е. баланс фаз нарушится и самовозбуждения
не произойдет.
приведет
к уменьшению коллекторного тока, т. е. баланс фаз нарушится и самовозбуждения
не произойдет.
Обратная связь (ОС), при которой выполняется баланс фаз, является положительной обратной связью. В противном случае обратная связь отрицательная. Самовозбуждение автогенератора возможно только при наличии положительной обратной связи.
Пока амплитуда напряжения ![]() была мала, работа происходила на линейном участке вольт-амперной характеристики
транзистора. С увеличением амплитуды колебаний на контуре возрастает напряжение
обратной связи
была мала, работа происходила на линейном участке вольт-амперной характеристики
транзистора. С увеличением амплитуды колебаний на контуре возрастает напряжение
обратной связи ![]() и, значит, входное напряжение транзистора
и, значит, входное напряжение транзистора ![]() .
При этом все сильнее сказывается нелинейность ВАХ транзистора. Наконец, при
достаточно больших амплитудах колебаний ток коллектора
.
При этом все сильнее сказывается нелинейность ВАХ транзистора. Наконец, при
достаточно больших амплитудах колебаний ток коллектора ![]() перестает увеличиваться, значения напряжения на контуре
перестает увеличиваться, значения напряжения на контуре ![]() ,
обратной связи
,
обратной связи ![]() и входное
и входное ![]() стабилизируются и в автогенераторе установится стационарный динамический
режим с постоянной амплитудой колебаний и частотой генерации, близкой к резонансной
частоте колебательного контура
стабилизируются и в автогенераторе установится стационарный динамический
режим с постоянной амплитудой колебаний и частотой генерации, близкой к резонансной
частоте колебательного контура ![]() .
Таким образом, стационарные колебания в автогенераторе устанавливаются только
благодаря наличию нелинейности вольт-амперной характеристики транзистора.
.
Таким образом, стационарные колебания в автогенераторе устанавливаются только
благодаря наличию нелинейности вольт-амперной характеристики транзистора.

Рассмотренный выше генератор содержит трансформатор и называется генератором с трансформаторной обратной связью, т. к. через трансформатор напряжение с выхода транзисторного усилительного каскада попадает на его вход. Можно сказать, что трансформатор представляет собой цепь обратной связи. Транзисторный усилительный каскад есть ни что иное, как нелинейный резонансный усилитель. Таким образом, автогенератор с трансформаторной обратной связью можно изобразить в виде усилителя, охваченного обратной связью (рис. 6.3). Обобщенная схема на рис. 6.3 справедлива и для других типов генераторов.
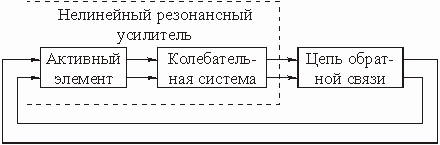
Рис. 6.3
Недостатком схем LC–генераторов
с трансформаторной обратной связью является наличие двух индуктивно связанных
катушек. Поэтому на практике используют схемы LC–генераторов с автотрансформаторной
обратной связью, в которых напряжение ОС снимается с части колебательного контура.
Такая схема изображена на рис. 6.4, а. Она известна также под названием
схемы индуктивной трехточки. Элементы С, ![]() и
и ![]() образуют
колебательный контур: резистор
образуют
колебательный контур: резистор ![]() является элементом цепи автоматического смещения, через который протекает постоянная
составляющая тока базы; конденсатор
является элементом цепи автоматического смещения, через который протекает постоянная
составляющая тока базы; конденсатор ![]() предотвращает попадание напряжения питания
предотвращает попадание напряжения питания ![]() на базу и влияет на постоянную времени цепи автосмещения. На рис. 6.4,
б приведена эквивалентная схема индуктивной трехточки по переменному
току, т. е. цепи питания и смещения на рисунке не показаны.
на базу и влияет на постоянную времени цепи автосмещения. На рис. 6.4,
б приведена эквивалентная схема индуктивной трехточки по переменному
току, т. е. цепи питания и смещения на рисунке не показаны.
Обычно полагают, что входное сопротивление
транзистора настолько велико, что током базы можно пренебречь. В этом случае,
как видно из рис. 6.4, б, элементы С, ![]() и
и ![]() образуют
трехэлементный колебательный контур, в котором сначала происходит резонанс токов,
а затем резонанс напряжений в контуре С
образуют
трехэлементный колебательный контур, в котором сначала происходит резонанс токов,
а затем резонанс напряжений в контуре С![]() .
Усилительный каскад со сложным колебательным контуром в коллекторной цепи транзистора
является нелинейным резонансным усилителем.
.
Усилительный каскад со сложным колебательным контуром в коллекторной цепи транзистора
является нелинейным резонансным усилителем.
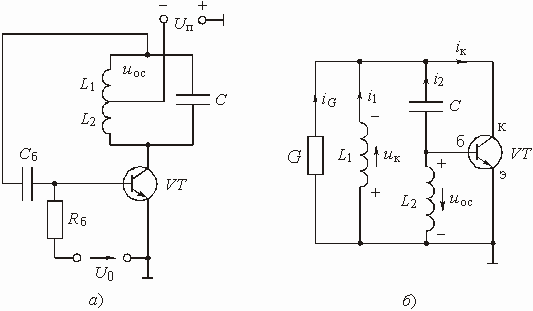
Рис. 6.4
Цепью обратной связи в этой схеме
служит делитель напряжения, образованный индуктивностью ![]() и индуктивностью
и индуктивностью ![]() .
Действительно, напряжение, снимаемое с выхода усилительного элемента (транзистора),
приложено к колебательному контуру или, что то же, к ветви
.
Действительно, напряжение, снимаемое с выхода усилительного элемента (транзистора),
приложено к колебательному контуру или, что то же, к ветви ![]() (рис. 6.4, б). Напряжение обратной связи снимается с индуктивности
(рис. 6.4, б). Напряжение обратной связи снимается с индуктивности ![]() и подается на вход усилительного элемента. Усилительный каскад на одном транзисторе
поворачивает фазу сигнала на 180° . Для соблюдения баланса фаз цепь обратной
связи также должна вносить фазовый сдвиг 180° . Это и происходит на самом
деле. Ток в ветви С
и подается на вход усилительного элемента. Усилительный каскад на одном транзисторе
поворачивает фазу сигнала на 180° . Для соблюдения баланса фаз цепь обратной
связи также должна вносить фазовый сдвиг 180° . Это и происходит на самом
деле. Ток в ветви С![]() из-за емкостного характера ее сопротивления опережает напряжение на контуре
из-за емкостного характера ее сопротивления опережает напряжение на контуре
![]() на 90°
. В свою очередь, напряжение
на 90°
. В свою очередь, напряжение ![]() на индуктивности
на индуктивности ![]() опережает этот ток еще на 90° . Таким образом, сдвиг фаз между напряжениями
опережает этот ток еще на 90° . Таким образом, сдвиг фаз между напряжениями
![]() и
и ![]() составляет 180° .
составляет 180° .
На сравнительно низких частотах, где реализация LC–контуров становится затруднительной из-за больших габаритов и массы, низкой добротности и невозможности перестройки, используют RC–автогенераторы. Они также представляют собой комбинацию усилителя и пассивной RC–цепи для создания обратной связи.
На рис. 6.5, а показана
схема такого генератора – однокаскадный транзисторный усилитель, между входом
и выходом которого включен лестничный пассивный ![]() четырехполюсник.
четырехполюсник.
Для возникновения генерации колебаний необходимо, чтобы напряжение обратной связи, подаваемое на вход генератора, непрерывно возрастало. Это возможно только тогда, когда усиление усилительного каскада больше ослабления, вносимого цепью обратной связи. Кроме того, должно выполняться условие баланса фаз. Последнее означает, что поскольку один каскад транзисторного усилителя вносит сдвиг фаз, равный 180° , то цепь обратной связи также должна вносить сдвиг фаз 180° , чтобы общий сдвиг фаз равнялся 0° (или 360° ).
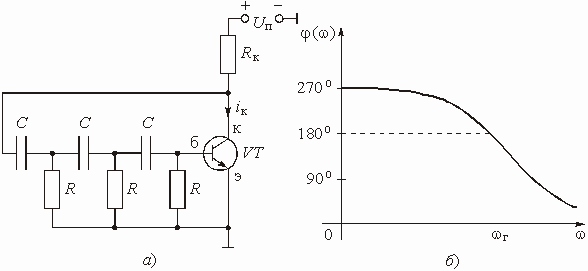
Рис. 6.5
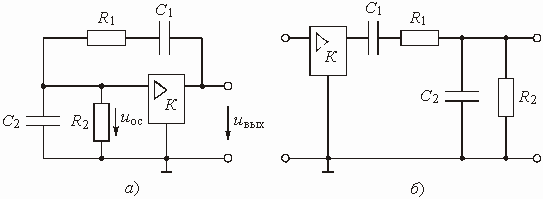
Рис. 6.6
Однако простейшее RC–звено вносит сдвиг фаз, не превышающий 90° . Поэтому необходимо взять число звеньев не меньше трех. Зависимость сдвига фаз от частоты RC–цепи из трех звеньев показана на рис. 6.5, б. Элементы RC–цепи рассчитывают так, чтобы на частоте генерации получить сдвиг фаз 180° .
В стационарном режиме, кроме баланса фаз, выполняется также и баланс амплитуд, т. е. усиление усилительного каскада становится равным ослаблению цепи обратной связи, так что амплитуда напряжения цепи обратной связи, а значит и выходного, остается постоянной.
На рис. 6.6, а и б
изображен еще один RC–автогенератор, носящий название автогенератора
с мостом Вина. Это усилитель с коэффициентом усиления ![]() ;
между его выходом и входом включена RC–цепь обратной связи. Как и в других
генераторах, для самовозбуждения колебаний необходимо, чтобы усиление усилителя
К было бы больше ослабления, вносимого в выходной сигнал усилителя RC–цепью
обратной связи. Усилитель не изменяет фазу сигнала, следовательно, чтобы обратная
связь была положительной и, тем самым, выполнялся баланс фаз, цепь обратной
связи также не должна изменять фазу сигнала.
;
между его выходом и входом включена RC–цепь обратной связи. Как и в других
генераторах, для самовозбуждения колебаний необходимо, чтобы усиление усилителя
К было бы больше ослабления, вносимого в выходной сигнал усилителя RC–цепью
обратной связи. Усилитель не изменяет фазу сигнала, следовательно, чтобы обратная
связь была положительной и, тем самым, выполнялся баланс фаз, цепь обратной
связи также не должна изменять фазу сигнала.

Анализ различных схем автогенераторов показывает, что все они могут быть представлены обобщенной структурой, показанной на рис. 6.7, а. При этом избирательная система (LC и RC–цепи) может быть включена либо в схему усилителя, либо в схему цепи обратной связи. Задача избирательной системы – отфильтровать ненужные гармонические составляющие, возникающие из-за нелинейности ВАХ, и обеспечить, тем самым, условия самовозбуждения автогенератора только на частоте генерации.
На рис. 6.7, б изображена
обобщенная схема автогенератора с разомкнутой цепью ОС. На входе усилителя действует
гармоническое напряжение с комплексной амплитудой ![]() .
Усилитель изменяет амплитуду и начальную фазу колебания и формирует напряжение
с комплексной амплитудой
.
Усилитель изменяет амплитуду и начальную фазу колебания и формирует напряжение
с комплексной амплитудой ![]() .
Коэффициент усиления усилителя
.
Коэффициент усиления усилителя ![]() равен отношению амплитуды выходного напряжения к амплитуде входного напряжения
равен отношению амплитуды выходного напряжения к амплитуде входного напряжения
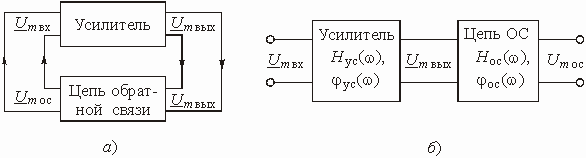
Рис. 6.7
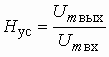 . (6.1)
. (6.1)
Усилитель добавляет к начальной
фазе входного гармонического напряжения фазовый сдвиг ![]() .
.
Цепь ОС ослабляет сигнал, действующий
на ее входе, до величины ![]() .
Коэффициент передачи цепи обратной связи равен
.
Коэффициент передачи цепи обратной связи равен
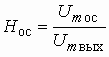 . (6.2)
. (6.2)
Фазовый сдвиг, вносимый этой цепью,
составляет величину ![]() .
.
Для того, чтобы после замыкания
цепи обратной связи в генераторе происходило самовозбуждение колебаний, необходимо,
чтобы на частоте генерации ![]() амплитуда гармонического напряжения на выходе схемы рис. 6.7, б была
больше амплитуды гармонического напряжения на входе схемы, т. е.
амплитуда гармонического напряжения на выходе схемы рис. 6.7, б была
больше амплитуды гармонического напряжения на входе схемы, т. е.
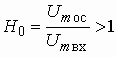 , (6.3)
, (6.3)
где ![]() – коэффициент передачи обобщенной схемы автогенератора с разомкнутой обратной
связью.
– коэффициент передачи обобщенной схемы автогенератора с разомкнутой обратной
связью.
Преобразуем выражение (6.3):
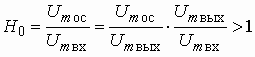 . (6.4)
. (6.4)
С учетом (6.1) и (6.2) получим
![]() . (6.5)
. (6.5)
Выражение (6.5) является фундаментальным в теории автоколебаний; оно применимо к любому типу генератора.
Таким образом, для самовозбуждения автогенератора необходимо, чтобы на частоте генерации усиление усилителя превышало ослабление, вносимое цепью обратной связи, т. е.
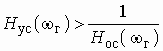 . (6.6)
. (6.6)
Условие (6.5), или (6.6), является необходимым, но недостаточным. Кроме него должен выполняться баланс фаз, т. е. совпадение начальных фаз гармонических напряжений на входе и выходе схемы рис. 6.7, б. Такое совпадение наступает, когда суммарный сдвиг фаз, вносимый усилителем и цепью обратной связи, равен нулю или кратен 360° :
![]() , (6.7)
, (6.7)
где К – целое число.
Таким образом, сдвиг фаз в цепи обратной связи зависит от сдвига фаз в усилителе и дополняет его до 360° .
Генератор с трансформаторной обратной
связью. Усилительным (активным) элементом в генераторе с трансформаторной обратной
связью является усилительный каскад на одном транзисторе с колебательным контуром
в коллекторной цепи. На рис. 6.8, а показана вольт-амперная характеристика
транзистора, представляющая зависимость тока коллектора ![]() от напряжения на участке « база – эмиттер»
от напряжения на участке « база – эмиттер» ![]() .
.
При выборе постоянного напряжения
смещения ![]() и отсутствии переменного напряжения на входе транзисторного усилительного каскада
(рис. 6.2) на участке « база – эмиттер» действует напряжение
и отсутствии переменного напряжения на входе транзисторного усилительного каскада
(рис. 6.2) на участке « база – эмиттер» действует напряжение ![]() .
В цепи коллектора транзистора протекает постоянный ток
.
В цепи коллектора транзистора протекает постоянный ток ![]() .
Предположим теперь, что на входе транзисторного каскада появилось гармоническое
напряжение с небольшой амплитудой
.
Предположим теперь, что на входе транзисторного каскада появилось гармоническое
напряжение с небольшой амплитудой ![]() ,
так что рабочая точка, смещаясь под действием переменного напряжения, остается
все время на линейном участке ВАХ. В этом случае в цепи коллектора наряду с
постоянным током будет протекать переменный ток.
,
так что рабочая точка, смещаясь под действием переменного напряжения, остается
все время на линейном участке ВАХ. В этом случае в цепи коллектора наряду с
постоянным током будет протекать переменный ток.
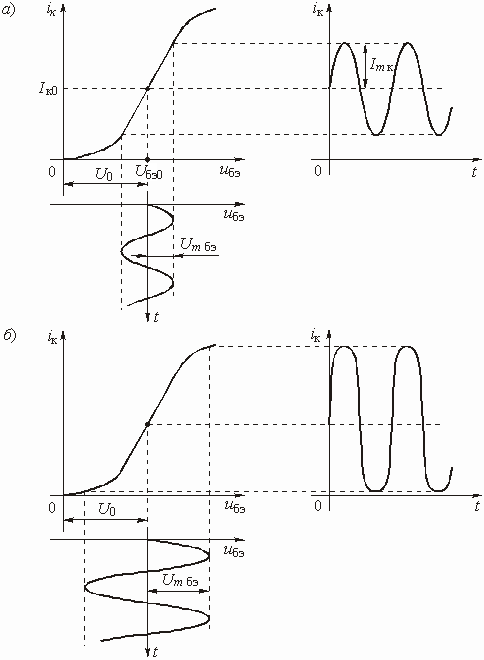
Рис. 6.8
Из-за линейного характера рабочего
участка ВАХ переменный ток в цепи коллектора будет гармоническим и будет иметь
ту же частоту, что и напряжение на участке « база – эмиттер» . Если
постоянно увеличивать амплитуду ![]() гармонического напряжения на входе транзистора (рис. 6.8, б), то наступит
момент, когда рабочая точка, перемещаясь под действием переменного напряжения,
начнет « захватывать» нелинейный участок ВАХ. Ток коллектора перестанет
тогда быть гармоническим. Помимо первой гармоники, имеющей ту же самую частоту,
что и входное напряжение, появятся высшие гармоники.
гармонического напряжения на входе транзистора (рис. 6.8, б), то наступит
момент, когда рабочая точка, перемещаясь под действием переменного напряжения,
начнет « захватывать» нелинейный участок ВАХ. Ток коллектора перестанет
тогда быть гармоническим. Помимо первой гармоники, имеющей ту же самую частоту,
что и входное напряжение, появятся высшие гармоники.
В случае, когда коллекторный ток
транзистора является гармоническим (рис. 6.8, а), напряжение, создаваемое
этим током на колебательном контуре, будет также гармоническим с амплитудой
![]() , где Z
– полное сопротивление контура на частоте гармонического колебания.
, где Z
– полное сопротивление контура на частоте гармонического колебания.
Коэффициент передачи (усиления) усилителя определяется отношением амплитуды выходного напряжения к амплитуде входного напряжения (рис. 6.7, б):
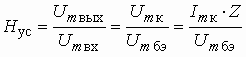 .
.
Отношение амплитуды гармонического
колебания тока к амплитуде гармонического колебания напряжения (при условии,
что эти амплитуды малы) называется дифференциальной крутизной ![]() вольт-амперной характеристики транзистора:
вольт-амперной характеристики транзистора:
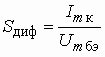 . (6.8)
. (6.8)
Пока рабочая точка не выходит за пределы линейного участка ВАХ, дифференциальная крутизна остается постоянной.
Таким образом коэффициент передачи
усилителя ![]() равен произведению дифференциальной крутизны ВАХ в рабочей точке
равен произведению дифференциальной крутизны ВАХ в рабочей точке ![]() и полного сопротивления колебательного контура Z на частоте гармонического
колебания:
и полного сопротивления колебательного контура Z на частоте гармонического
колебания:
![]() . (6.9)
. (6.9)
При больших амплитудах ![]() напряжения на входе транзистора (рис.6.8, б) ток коллектора перестает
быть гармоническим и определение дифференциальной крутизны из (6.8) теряет смысл.
Обычно вместо дифференциальной крутизны используют понятие средней крутизны,
или крутизны по первой гармонике, т. е. отношение амплитуды первой гармоники
коллекторного тока к амплитуде входного напряжения. Обозначим амплитуду первой
гармоники
напряжения на входе транзистора (рис.6.8, б) ток коллектора перестает
быть гармоническим и определение дифференциальной крутизны из (6.8) теряет смысл.
Обычно вместо дифференциальной крутизны используют понятие средней крутизны,
или крутизны по первой гармонике, т. е. отношение амплитуды первой гармоники
коллекторного тока к амплитуде входного напряжения. Обозначим амплитуду первой
гармоники ![]() .
Тогда вместо (6.8) будем иметь
.
Тогда вместо (6.8) будем иметь
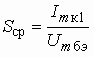 . (6.10)
. (6.10)
Если колебательный контур построен таким образом, что его резонансная частота
![]()
совпадает с частотой первой гармоники
тока коллектора, то полное сопротивление контура на этой частоте будет максимальным
и равным R = 1/G, а на частотах, отличных от резонансной,
оно будет уменьшаться. При больших добротностях Q колебательного контура
его полное сопротивление станет настолько малым для всех высших гармоник тока,
начиная со второй, что эти гармоники не создадут практически никакого напряжения
на контуре. Амплитуда напряжения на контуре будет определяться только амплитудой
первой гармоники тока: ![]() .
.
Коэффициент передачи усилительного каскада в этом случае определится как
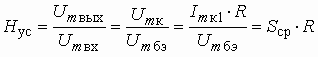 . (6.11)
. (6.11)
Данное выражение справедливо только
для резонансной частоты ![]() .
На других частотах при достаточно высокой добротности контура коэффициент усиления
усилителя резко уменьшается. Следовательно, самовозбуждение генератора может
произойти только на частоте резонанса колебательного контура, т. е. частота
генерации
.
На других частотах при достаточно высокой добротности контура коэффициент усиления
усилителя резко уменьшается. Следовательно, самовозбуждение генератора может
произойти только на частоте резонанса колебательного контура, т. е. частота
генерации ![]() .
.
Цепь обратной связи в генераторе
на рис. 6.2, ослабляющая сигнал, подводимый к усилителю, представляет собой
трансформатор с первичной обмоткой, имеющей индуктивность L, вторичной
обмоткой с индуктивностью ![]() и взаимной индуктивностью М.
и взаимной индуктивностью М.
Из теории трансформатора известно, что напряжение, наводимое первичной обмоткой во вторичной, зависит от взаимной индуктивности М:
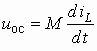 .
.
В свою очередь, напряжение на первичной обмотке (т. е. на контуре) зависит от ее индуктивности L:
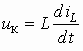 .
.
Следовательно, напряжение на вторичной обмотке можно выразить через напряжение на колебательном контуре:
![]() . (6.12)
. (6.12)
Наличие связи (6.12) между мгновенными значениями напряжения позволяет сразу же установить связь между амплитудами этих напряжений:
![]() .
.
Коэффициент передачи цепи обратной связи, как это следует из рис. 6.7, б, равен
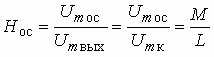 . (6.13)
. (6.13)
Он не зависит от частоты и поэтому одинаков на всех частотах.
Условие самовозбуждения генератора (6.5), или (6.6) примет в данном случае вид:
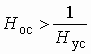 или
или ![]() . (6.14)
. (6.14)
В реальных схемах генераторов выполнение условия (6.14) обеспечивают изменением взаимной индуктивности М. Поэтому данное условие записывают обычно в виде
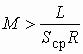 .
.
Величина
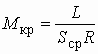 (6.15)
(6.15)
называется критическим коэффициентом
взаимной индукции. Колебания в генераторе могут возникнуть только при обратной
связи с ![]() .
.
Второе условие возникновения колебаний (6.7) означает, что в схеме генератора должен выполняться баланс фаз. Известно, что однокаскадный усилитель (усилитель на одном транзисторе) « переворачивает» сигнал, т. е. вносит сдвиг фаз 180° . Чтобы сдвиг фаз в цепи обратной связи дополнял сдвиг фаз в усилителе до 360° , т. е. равнялся также 180° , необходимо переполюсовать вторичную обмотку трансформатора таким образом, чтобы напряжение на ней было перевернуто относительно напряжения на первичной обмотке.
Генератор с автотрансформаторной
обратной связью (индуктивная трехточка). В данной схеме генератора (рис. 6.4)
усилительный каскад собран на одном транзисторе, в коллекторную цепь которого
включен трехэлементный колебательный контур из элементов ![]() ,
,
![]() и С.
Ток базы транзистора обычно принимается равным нулю, т. е. входное сопротивление
транзистора считается достаточно большим и, следовательно, транзистор не влияет
на работу контура.
и С.
Ток базы транзистора обычно принимается равным нулю, т. е. входное сопротивление
транзистора считается достаточно большим и, следовательно, транзистор не влияет
на работу контура.
Из теории реактивных двухполюсников известно, что на частоте
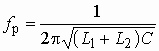 (6.16)
(6.16)
в данном колебательном контуре
возникает резонанс токов, полное сопротивление становится максимальным и равным
R = 1/G. Эта частота и выбирается в качестве частоты генерации:
![]() .
.
Усиление транзисторного каскада на резонансной частоте определяется, как и в схеме с трансформаторной обратной связью, формулой (6.11):
![]() , (6.17)
, (6.17)
где ![]() – средняя крутизна ВАХ в рабочей точке, совпадающая с дифференциальной крутизной
– средняя крутизна ВАХ в рабочей точке, совпадающая с дифференциальной крутизной
![]() при малых
амплитудах гармонического напряжения на входе транзистора.
при малых
амплитудах гармонического напряжения на входе транзистора.
Коэффициент передачи цепи обратной связи (рис. 6.7, б) равен
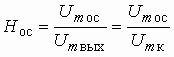 .
.
Напряжение обратной связи, подаваемое
на вход транзистора, снимается с индуктивности ![]() и имеет амплитуду
и имеет амплитуду ![]() .
Амплитуду напряжения на входе усилителя, или, что то же, на колебательном контуре,
можно вычислить по формуле
.
Амплитуду напряжения на входе усилителя, или, что то же, на колебательном контуре,
можно вычислить по формуле ![]() .
Тогда
.
Тогда
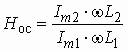 .
.
На частоте резонанса токов (6.16),
которая и является частотой генерации ![]() ,
амплитуды токов в реактивных ветвях равны по величине, т. е.
,
амплитуды токов в реактивных ветвях равны по величине, т. е. ![]() .
Следовательно,
.
Следовательно,
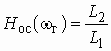 . (6.18)
. (6.18)
Условие самовозбуждения (6.6) запишется с учетом (6.17) и (6.18) в следующем виде:
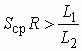 .
.
Данное условие позволяет подобрать
такое отношение индуктивностей ![]() и
и ![]() , при котором
в генераторе могут возникнуть гармонические колебания. Частота генерации подстраивается
согласно (6.16) изменением величины емкости С.
, при котором
в генераторе могут возникнуть гармонические колебания. Частота генерации подстраивается
согласно (6.16) изменением величины емкости С.
Усилительный каскад на одном транзисторе
вносит сдвиг фаз 180° . Для самовозбуждения генератора такой же сдвиг фаз
должна вносить цепь обратной связи. Это и происходит на самом деле, поскольку
токи в реактивных ветвях контура в момент резонанса токов находятся в противофазе
и, значит, напряжения на индуктивных элементах ![]() и
и ![]() также находятся
в противофазе.
также находятся
в противофазе.
RC–генератор с лестничной
цепью обратной связи. Схема генератора изображена на рис. 6.5, а.
В цепь коллектора транзистора включено резистивное сопротивление ![]() .
Усиление транзисторного каскада на любой частоте равно произведению средней
крутизны ВАХ в рабочей точке и сопротивления коллекторной цепи:
.
Усиление транзисторного каскада на любой частоте равно произведению средней
крутизны ВАХ в рабочей точке и сопротивления коллекторной цепи:
![]() .
.
Транзисторный каскад вносит сдвиг фаз 180° .
По-прежнему считаем входное сопротивление транзистора настолько большим, что он не влияет на работу цепи обратной связи.
Из теории черытехполюсников известно, что передаточная функция лестничной цепи, изображенной на рис. 6.5, а, описывается выражением:
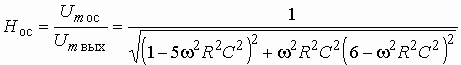 . (6.19)
. (6.19)
Необходимо, чтобы цепь обратной связи вносила на частоте генерации фазовый сдвиг 180° . Можно показать, что это произойдет, если выбрать частоту генерации равной
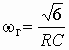 .
.
Подставив данную формулу в (6.19), легко убедиться, что передаточная функция цепи обратной связи будет равна
![]() .
.
Тогда из (6.6) получим условие
самовозбуждения на частоте ![]() :
:
![]() , (6.20)
, (6.20)
т. е. для возникновения в RC–генераторе колебаний усиление транзисторного каскада должно быть больше 29 единиц.
RC–генератор с мостом Вина. Схема генератора дана на рис. 6.6, а. Усилитель, выполненный на транзисторах или операционном усилителе, имеет независимый от частоты коэффициент передачи К. Между выходом и входом усилителя включен четырехполюсник обратной связи в виде RC–цепи. Схема генератора с разомкнутой обратной связью приведена на рис. 6.6, б.
Коэффициент передачи четырехполюсника обратной связи имеет вид:
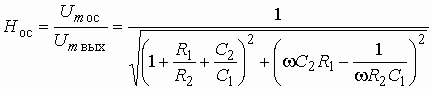 . (6.21)
. (6.21)
Поскольку усилитель не вносит фазового сдвига, для выполнения условия баланса фаз требуется, чтобы цепь обратной связи также не вносила никакого фазового сдвига. Известно, что RC–четырехполюсник на рис. 6.6, б вносит нулевой сдвиг фаз на частоте
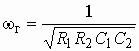 .
.
На этой частоте будет происходить генерация колебаний.
Подстановка выражения для ![]() в (6.21) дает значение коэффициента передачи цепи обратной связи на частоте
генерации:
в (6.21) дает значение коэффициента передачи цепи обратной связи на частоте
генерации:
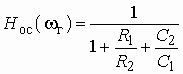 .
.
Условие самовозбуждения на частоте
генерации ![]() примет вид:
примет вид:
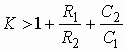 . (6.22)
. (6.22)
Если выбрать ![]() и
и ![]() , то условие
возникновения колебаний упростится: К > 3. В этом случае гармонические
колебания с частотой
, то условие
возникновения колебаний упростится: К > 3. В этом случае гармонические
колебания с частотой ![]() возникнут в генераторе, когда усиление усилителя будет больше 3 единиц.
возникнут в генераторе, когда усиление усилителя будет больше 3 единиц.

В усилителях на транзисторе передаточная функция определяется, как было показано выше, выражением
![]() , (6.23)
, (6.23)
где ![]() – сопротивление нагрузки усилителя (резонансное сопротивление контура, коллекторное
сопротивление и т. п.).
– сопротивление нагрузки усилителя (резонансное сопротивление контура, коллекторное
сопротивление и т. п.).
Рис. 6.9
Средняя крутизна ![]() зависит от амплитуды напряжения на входе транзистора
зависит от амплитуды напряжения на входе транзистора ![]() и от положения рабочей точки
и от положения рабочей точки ![]() .
На рис. 6.9 показана типичная ВАХ транзистора
.
На рис. 6.9 показана типичная ВАХ транзистора ![]() .
Пусть рабочая точка выбрана на середине линейного участка характеристики (
.
Пусть рабочая точка выбрана на середине линейного участка характеристики (![]() ).
При увеличении амплитуды напряжения
).
При увеличении амплитуды напряжения ![]() средняя крутизна, пока мы находимся в пределах линейного участка характеристики,
остается неизменной. Затем средняя крутизна ВАХ падает (рис. 6.10, а).
средняя крутизна, пока мы находимся в пределах линейного участка характеристики,
остается неизменной. Затем средняя крутизна ВАХ падает (рис. 6.10, а).
Если выбрать рабочую точку (![]() )
на нижнем загибе характеристики
)
на нижнем загибе характеристики ![]() ,
где средняя крутизна мала, то по мере увеличения амплитуды
,
где средняя крутизна мала, то по мере увеличения амплитуды ![]() будут охватываться участки характеристики с большей крутизной и, следовательно,
будут охватываться участки характеристики с большей крутизной и, следовательно,
![]() будет расти.
После прохождения участка с наибольшей крутизной дальнейшее увеличение приводит
к уменьшению средней крутизны (рис. 6.10, б).
будет расти.
После прохождения участка с наибольшей крутизной дальнейшее увеличение приводит
к уменьшению средней крутизны (рис. 6.10, б).
Рис. 6.10
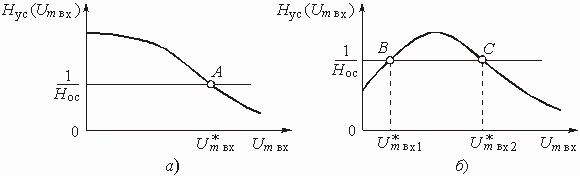
Рис. 6.11
Из выражения (6.23) следует, что
усиление транзисторного усилителя также зависит от амплитуды напряжения на входе
транзистора и от положения рабочей точки. На рис. 6.11, а и б
показаны графики ![]() в зависимости от амплитуды
в зависимости от амплитуды ![]() для двух положений рабочей точки на ВАХ, соответствующих рис. 6.9.
для двух положений рабочей точки на ВАХ, соответствующих рис. 6.9.

Условие (6.6)
![]()
соответствует появлению в генераторе
гармонических колебаний с нарастающей амплитудой. Смена знака в этом неравенстве
на обратный, т. е. ![]() будет означать, что гармонические колебания в генераторе затухают по амплитуде.
Установившемуся, или стационарному режиму, соответствует равенство
будет означать, что гармонические колебания в генераторе затухают по амплитуде.
Установившемуся, или стационарному режиму, соответствует равенство
![]() . (6.24)
. (6.24)
Кроме того, на частоте генерации
должен выполняться баланс фаз: ![]() .
.
Равенство (6.24) удобно иллюстрировать
графически. Сначала строится график зависимости усиления усилителя ![]() от амплитуды
от амплитуды ![]() сигнала на его входе (рис. 6.11), а затем проводится прямая линия на уровне
сигнала на его входе (рис. 6.11), а затем проводится прямая линия на уровне
![]() . Перпендикуляр,
опущенный из точки пересечения линий на ось абсцисс, указывает на установившееся
(стационарное) значение амплитуды
. Перпендикуляр,
опущенный из точки пересечения линий на ось абсцисс, указывает на установившееся
(стационарное) значение амплитуды ![]() гармонического колебания на входе усилителя.
гармонического колебания на входе усилителя.
На рис. 6.11, б прямая
линия ![]() пересекает
кривую усиления в двух точках В и С, которым соответствуют две
установившиеся (стационарные) амплитуды колебаний
пересекает
кривую усиления в двух точках В и С, которым соответствуют две
установившиеся (стационарные) амплитуды колебаний ![]() и
и ![]() .
.
Установившийся режим работы генератора
называется устойчивым, если отклонение амплитуды ![]() от установившегося значения
от установившегося значения ![]() с течением времени будет уменьшаться.
с течением времени будет уменьшаться.
Рассмотрим установившийся режим
в точке А на рис. 6.11, а. Уменьшение амплитуды напряжения ![]() ,
т. е. отклонение
,
т. е. отклонение ![]() влево от значения
влево от значения ![]() приведет к выполнению неравенства
приведет к выполнению неравенства
![]() .
.
В результате амплитуда колебаний
будет увеличиваться и приближаться к установившемуся значению. При увеличении
амплитуды напряжения ![]() ,
т. е. при отклонении
,
т. е. при отклонении ![]() вправо от
вправо от ![]() будет выполняться неравенство
будет выполняться неравенство
![]()
и амплитуда ![]() уменьшится, вновь приближаясь к установившемуся значению
уменьшится, вновь приближаясь к установившемуся значению ![]() .
.
Точка В на рис. 6.11, б
соответствует неустойчивому установившемуся режиму, так как отклонение амплитуды
![]() от установившегося
значения
от установившегося
значения ![]() в сторону уменьшения ведет в силу неравенства
в сторону уменьшения ведет в силу неравенства
![]()
к дальнейшему уменьшению амплитуды
![]() и, в конечном
счете, к срыву колебаний, а отклонение амплитуды
и, в конечном
счете, к срыву колебаний, а отклонение амплитуды ![]() от установившегося значения
от установившегося значения ![]() в сторону увеличения вызовет дальнейший ее рост так как
в сторону увеличения вызовет дальнейший ее рост так как
![]() ,
,
и переход в следующее установившееся состояние, отмеченное точкой С. Установившееся состояние в точке С является устойчивым, в чем легко убедиться с помощью рассуждений, аналогичных приведенным выше.
Можно заметить, что справедливо
следующее утверждение: пересечение прямой линии ![]() с кривой усиления
с кривой усиления ![]() дает устойчивое установившееся значение амплитуды гармонических колебаний на
входе усилителя
дает устойчивое установившееся значение амплитуды гармонических колебаний на
входе усилителя ![]() ,
если касательная к кривой
,
если касательная к кривой ![]() в стационарной точке имеет отрицательный угол наклона, и неустойчивое значение
– если угол наклона касательной является положительным.
в стационарной точке имеет отрицательный угол наклона, и неустойчивое значение
– если угол наклона касательной является положительным.
По графикам на рис. 6.11 определяется
амплитуда установившегося гармонического колебания на входе усилителя. Для того,
чтобы определить амплитуду установившегося гармонического колебания на выходе
усилителя, или, что то же, на выходе генератора (рис. 6.7), нужно амплитуду
напряжения на входе усилителя умножить на коэффициент усиления усилителя ![]() в установившемся режиме:
в установившемся режиме:
![]() .
.

Будем менять величину ![]() и наблюдать за процессом возникновения колебаний. Этот процесс зависит также
от выбора рабочей точки на вольт-амперной характеристике (напряжения смещения
и наблюдать за процессом возникновения колебаний. Этот процесс зависит также
от выбора рабочей точки на вольт-амперной характеристике (напряжения смещения
![]() ).
).
Выбору рабочей точки в области
наибольшей крутизны (напряжение смещения ![]() на рис. 6.9) соответствует график
на рис. 6.9) соответствует график ![]() ,
показанный на рис. 6.11, а.
,
показанный на рис. 6.11, а.
Рис. 6.14
На рис. 6.14, а изображены
несколько прямых, соответствующих различным значениям ![]() .
.
При ![]() колебания в автогенераторе возникнуть не могут, поскольку
колебания в автогенераторе возникнуть не могут, поскольку ![]() ,
значит, любые случайные флуктуации напряжения
,
значит, любые случайные флуктуации напряжения ![]() будут быстро затухать.
будут быстро затухать.
Увеличение ![]() до значения
до значения ![]() приводит к условию
приводит к условию ![]() .
Дальнейшее увеличение
.
Дальнейшее увеличение ![]() усиливает
неравенство
усиливает
неравенство ![]() и, таким образом, начиная с
и, таким образом, начиная с ![]() Õ
Õ ![]() , в
автогенераторе возникают незатухающие гармонические колебания с соответствующими
установившимися амплитудами на входе усилителя
, в
автогенераторе возникают незатухающие гармонические колебания с соответствующими
установившимися амплитудами на входе усилителя ![]() .
С увеличением
.
С увеличением ![]() установившаяся амплитуда
установившаяся амплитуда ![]() гармонических колебаний плавно нарастает. Уменьшение
гармонических колебаний плавно нарастает. Уменьшение ![]() вызовет плавное уменьшение значений установившейся амплитуды
вызовет плавное уменьшение значений установившейся амплитуды ![]() .
.
График зависимости установившейся
амплитуды ![]() гармонического колебания на входе усилителя от коэффициента передачи
гармонического колебания на входе усилителя от коэффициента передачи ![]() цепи обратной связи приведен на рис. 6.14, б. Такой режим самовозбуждения,
при котором амплитуда колебаний плавно нарастает с увеличением
цепи обратной связи приведен на рис. 6.14, б. Такой режим самовозбуждения,
при котором амплитуда колебаний плавно нарастает с увеличением ![]() ,
называется мягким режимом самовозбуждения.
,
называется мягким режимом самовозбуждения.
Если рабочую точку выбрать на нижнем
загибе ВАХ, как это показано на рис. 6.9, при ![]() ,
то график
,
то график ![]() имеет вид, показанный на рис. 6.15, а.
имеет вид, показанный на рис. 6.15, а.
Рис. 6.15
При значениях ![]() ,
равных
,
равных ![]() ,
, ![]() и
и ![]() , наличие
малых флуктуаций напряжения
, наличие
малых флуктуаций напряжения ![]() не приведет к установившемуся режиму работы генератора, поскольку при этих значениях
не приведет к установившемуся режиму работы генератора, поскольку при этих значениях
![]() будет иметь
место неравенство
будет иметь
место неравенство ![]() .
.
Только начиная с ![]() ,
когда
,
когда ![]() Õ
Õ
![]() , малые флуктуации
амплитуды напряжения
, малые флуктуации
амплитуды напряжения ![]() начинают быстро расти, пока не установится устойчивое стационарное значение
амплитуды колебаний
начинают быстро расти, пока не установится устойчивое стационарное значение
амплитуды колебаний ![]() .
Дальнейшее увеличение
.
Дальнейшее увеличение ![]() ведет к плавному росту амплитуды установившегося в генераторе колебания.
ведет к плавному росту амплитуды установившегося в генераторе колебания.
При плавном уменьшении коэффициента
передачи цепи обратной связи амплитуда ![]() установившегося гармонического колебания будет также плавно уменьшатся. Колебания
сорвутся при значении
установившегося гармонического колебания будет также плавно уменьшатся. Колебания
сорвутся при значении ![]() ,
меньшем
,
меньшем ![]() ,
когда перестанет выполняться условие
,
когда перестанет выполняться условие ![]() Õ
Õ ![]() . На
рис. 6.15, б дан график изменения стационарной амплитуды
. На
рис. 6.15, б дан график изменения стационарной амплитуды ![]() в зависимости от
в зависимости от ![]() .
Такой режим, когда колебания возбуждаются при большем значении
.
Такой режим, когда колебания возбуждаются при большем значении ![]() ,
а срываются при меньшем значении
,
а срываются при меньшем значении ![]() ,
называется жестким режимом самовозбуждения.
,
называется жестким режимом самовозбуждения.
Достоинством мягкого режима самовозбуждения
является плавное изменение амплитуды ![]() при изменении коэффициента передачи
при изменении коэффициента передачи ![]() .
Достоинством жесткого режима является высокий КПД за счет работы с отсечкой
коллекторного тока.
.
Достоинством жесткого режима является высокий КПД за счет работы с отсечкой
коллекторного тока.
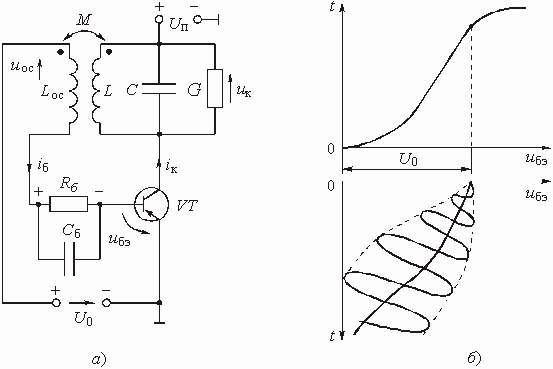
Рис. 6.16
Можно объединить достоинства мягкого
и жесткого режимов самовозбуждения, если ввести в автогенератор цепь автоматического
смещения ![]()
![]() (рис. 6.16, а). Исходное смещение
(рис. 6.16, а). Исходное смещение ![]() выбирают таким, чтобы рабочая точка находилась на участке наибольшей крутизны
ВАХ, что соответствует мягкому режиму. При нарастании амплитуды колебаний
выбирают таким, чтобы рабочая точка находилась на участке наибольшей крутизны
ВАХ, что соответствует мягкому режиму. При нарастании амплитуды колебаний ![]() в цепи базы за счет нелинейности ВАХ
в цепи базы за счет нелинейности ВАХ ![]() будет происходить детектирование колебаний. Возрастание постоянной составляющей
тока базы
будет происходить детектирование колебаний. Возрастание постоянной составляющей
тока базы ![]() ,
которая на активном сопротивлении
,
которая на активном сопротивлении ![]() создает напряжение
создает напряжение ![]() ×
×
![]() , приведет
к уменьшению результирующего напряжения смещения
, приведет
к уменьшению результирующего напряжения смещения ![]() –
– ![]() ×
×
![]() и, как результат,
к сдвигу рабочей точки влево (рис. 6.16, б) к нижнему загибу вольт-амперной
характеристики
и, как результат,
к сдвигу рабочей точки влево (рис. 6.16, б) к нижнему загибу вольт-амперной
характеристики ![]() .
Переходный процесс заканчивается (при соответствующей величине
.
Переходный процесс заканчивается (при соответствующей величине ![]() )
установлением жесткого стационарного режима с более высоким КПД.
)
установлением жесткого стационарного режима с более высоким КПД.
Примеры к главе 6
Пример 6.1
Рассчитать значение коэффициента
передачи цепи обратной связи ![]() ,
при котором наступает самовозбуждение автогенератора (рис. 6.2), а также частоту
генерации
,
при котором наступает самовозбуждение автогенератора (рис. 6.2), а также частоту
генерации ![]() ,
если заданы параметры элементов контура L = 100 мкГн, С = 0,1
мкФ, R = 20 кОм и средняя крутизна ВАХ транзистора
,
если заданы параметры элементов контура L = 100 мкГн, С = 0,1
мкФ, R = 20 кОм и средняя крутизна ВАХ транзистора ![]() = 4 мА/В.
= 4 мА/В.
Из условия (6.14) следует, что самовозбуждение автогенератора наступает при
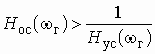 .
.
Рассчитаем коэффициент передачи
усилителя ![]() по формуле (6.11):
по формуле (6.11):
![]() .
.
Найдем ![]() :
:
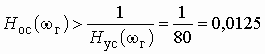 .
.
Самовозбуждение автогенератора
наступает при ![]() > > 0,0125.
> > 0,0125.
Частотой генерации колебаний является резонансная частота колебательного контура, поэтому
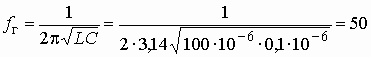 кГц.
кГц.
Пример 6.2
Рассчитать значение
критического коэффициента взаимной индукции автогенератора (рис. 6.2), если
заданы параметры элементов контура L
= 100 мкГн, R = 10 кОм и коэффициент передачи усилителя ![]() .
.
Рассчитаем вначале крутизну ВАХ транзистора. Из формулы (6.11) имеем
![]() 2 мА/В.
2 мА/В.
Критический коэффициент взаимной индукции рассчитаем по формуле (6.15):
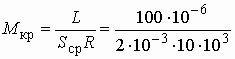 = 5 мкГн.
= 5 мкГн.
Колебания в контуре могут возникнуть только при M > 5 мкГн.
Пример 6.3
Рассчитать крутизну характеристики транзистора, при которой наступит самовозбуждение автогенератора (рис. 6.2), если заданы емкость и сопротивление контура C = 10 нФ, R = 5 кОм, добротность контура Q = 10, а также взаимная индуктивность M = 100 мкГн.
Из теории параллельного колебательного контура известно, что
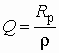 ,
,
где ![]() – сопротивление контура на резонансной частоте, r – характеристическое
сопротивление контура
– сопротивление контура на резонансной частоте, r – характеристическое
сопротивление контура ![]() .
.
Зная значения Q = 10, ![]() = R = 5 кОм, С = 10 нФ, найдем значение L:
= R = 5 кОм, С = 10 нФ, найдем значение L:
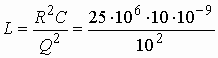 = 2,5 мГн.
= 2,5 мГн.
Для расчета крутизны ВАХ транзистора воспользуемся условием самовозбуждения (6.14). Получаем
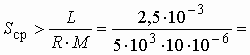 5 мА/В.
5 мА/В.
Крутизна ![]() проходной ВАХ транзистора должна быть больше 5 мА/В, чтобы наступило самовозбуждение
автогенератора.
проходной ВАХ транзистора должна быть больше 5 мА/В, чтобы наступило самовозбуждение
автогенератора.
Пример 6.4
Рассчитать минимальное значение
коэффициента передачи ![]() усилителя, при котором происходит самовозбуждение автогенератора, схема которого
приведена на рис. 6.4, б, а также частоту генерации
усилителя, при котором происходит самовозбуждение автогенератора, схема которого
приведена на рис. 6.4, б, а также частоту генерации ![]() ,
если заданы параметры элементов контура
,
если заданы параметры элементов контура ![]() = 15 мкГн,
= 15 мкГн, ![]() =
6 мкГн, С = 0,1 мкФ.
=
6 мкГн, С = 0,1 мкФ.
Рассчитаем коэффициент передачи
цепи обратной связи ![]() по формуле (6.18)
по формуле (6.18)
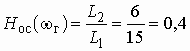 .
.
Из условия самовозбуждения автогенератора (6.5) получаем
![]() >
> 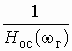 .
.
Рассчитаем значение
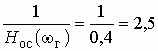 .
.
Самовозбуждение автогенератора
может наступить только при ![]() > 2,5.
> 2,5.
Частоту генерации рассчитаем, используя формулу (6.16):
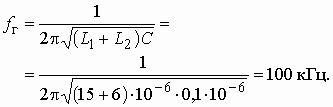
Пример 6.5
Рассчитать значение сопротивления
![]() в коллекторной
цепи, при котором произойдет самовозбуждение автогенератора (рис. 6.5, а),
а также частоту генерируемых колебаний, если заданы параметры элементов цепи
обратной связи С = 200 пФ, R = 20 кОм и средняя крутизна ВАХ транзистора
в коллекторной
цепи, при котором произойдет самовозбуждение автогенератора (рис. 6.5, а),
а также частоту генерируемых колебаний, если заданы параметры элементов цепи
обратной связи С = 200 пФ, R = 20 кОм и средняя крутизна ВАХ транзистора
![]() = 65 мА/В.
= 65 мА/В.
Из условия самовозбуждения (6.20)
найдем значение ![]() :
:
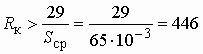 Ом.
Ом.
Для того, чтобы произошло самовозбуждение
автогенератора необходимо, чтобы ![]() было больше 446 Ом.
было больше 446 Ом.
Частота генерации ![]() рассчитывается по формуле
рассчитывается по формуле
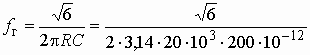 = 97 кГц.
= 97 кГц.
Пример 6.6
Рассчитать значение емкости ![]() в цепи обратной связи автогенератора (рис. 6.6, а) и частоту генерации
в цепи обратной связи автогенератора (рис. 6.6, а) и частоту генерации
![]() , если заданы
параметры элементов
, если заданы
параметры элементов ![]() 20 кОм,
20 кОм, ![]() =
10 кОм,
=
10 кОм, ![]() =
7 нФ и коэффициент усиления усилителя К = 4.
=
7 нФ и коэффициент усиления усилителя К = 4.
Значение емкости ![]() найдем из условия самовозбуждения (6.22):
найдем из условия самовозбуждения (6.22):
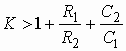 .
.
Отсюда
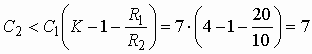 нФ.
нФ.
Для того, чтобы произошло самовозбуждение
автогенератора, необходимо чтобы емкость ![]() была меньше 7 нФ.
была меньше 7 нФ.
Частота генерации рассчитывается по формуле
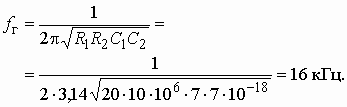
Пример 6.7
Рассчитать амплитуду стационарного
колебания на выходе автогенератора (рис. 6.2), если заданы L = 100 мкГн,
М = 10 мкГн, G = ![]() См, а также график зависимости
См, а также график зависимости ![]() – на рис. 6.12.
– на рис. 6.12.
Рассчитываем коэффициент передачи цепи обратной связи по формуле (6.43)
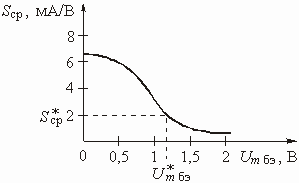
Рис. 6.12
![]() .
.
Рассчитываем коэффициент передачи усилителя, при котором в автогенераторе существуют стационарные колебания:
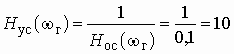 .
.
Из условия (6.23) находим значение стационарной средней крутизны
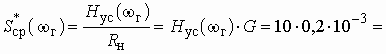 2 мА/В.
2 мА/В.
По графику 6.12 определяем амплитуду стационарного колебания на входе усилителя
![]() 1,2 В.
1,2 В.
Рассчитываем амплитуду стационарного колебания на выходе автогенератора
![]() 12 В.
12 В.
Пример 6.8
Определить амплитуду стационарного
колебания на выходе автогенератора (рис. 6.4, б), если заданы индуктивности
![]() = 15 мкГн,
= 15 мкГн,
![]() = 5 мкГн
и колебательная характеристика (рис. 6.13) автогенератора.
= 5 мкГн
и колебательная характеристика (рис. 6.13) автогенератора.
Рассчитываем коэффициент передачи
цепи ОС ![]() автогенератора
по формуле (6.18)
автогенератора
по формуле (6.18)
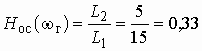 .
.
Из баланса амплитуд коэффициент передачи усилителя
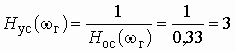 .
.
Рис. 6.13
По колебательной характеристике
(рис. 6.13) определяем амплитуду стационарного колебания на входе усилителя.
Следует отметить, что прямая ![]() пересекает колебательную характеристику в точке С, причем этот режим
является устойчивым, поэтому
пересекает колебательную характеристику в точке С, причем этот режим
является устойчивым, поэтому
![]() = 0,6 В.
= 0,6 В.
Амплитуда стационарного колебания на выходе автогенератора определяется по формуле
![]() 1, 8 В.
1, 8 В.
Вопросы и задания для самопроверки
1. Каким образом в автогенераторе (рис. 6.2) возникают стационарные гармонические колебания?
2. Пояснить принцип работы автогенератора по рис. 6.3.
3. Какие типы автогенераторов существуют? Как работают эти генераторы?
4. Сформулировать условия самовозбуждения автогенераторов: а) с трансформаторной обратной связью; б) индуктивной трехточки; в) RC-генератора с лестничной цепью обратной связи; г) RC-генератора с мостом Вина.
5. Проверить, произойдет ли самовозбуждение автогенератора (рис. 6.2), если L =
200 мкГн, М
= 50 мкГн, ![]() =
10 кОм,
=
10 кОм, ![]() =
1 мА/В.
=
1 мА/В.
|
Рис. 6.17 |
Ответ: да.
6. Является ли цепь на рис.
6.4, б автогенератором, если ![]() =
2,5;
=
2,5; ![]() = 30
мкГн;
= 30
мкГн; ![]() =
10 мкГн?
=
10 мкГн?
Ответ: нет.
7. Рассчитать значение крутизны
характеристики транзистора, при котором произойдет самовозбуждение RC-автогенератора с лестничной цепью обратной связи, если ![]() =
0,5 кОм.
=
0,5 кОм.
Ответ: ![]() >
58 мА/В.
>
58 мА/В.
8. Как рассчитывается частота генерируемых колебаний в автогенераторах разных типов?
9. Рассчитать частоту генерации
колебаний в -генераторе с мостом Вина, если ![]() =
7 нФ,
=
7 нФ, ![]() =
10 кОм.
=
10 кОм.
Ответ:
![]() =
2,27 кГц.
=
2,27 кГц.
10. Какими будут графики зависимости средней крутизны (или коэффициента передачи усилителя) от напряжения на входе усилителя при разных положениях рабочей точки на ВАХ (в середине линейного участка и на нижнем загибе)?
11. Сформулировать условия баланса амплитуд и баланса фаз в установившемся режиме.
12. Каким образом по колебательной характеристике (рис. 6.11) определяется амплитуда стационарных колебаний?
13. Определить амплитуду стационарного колебания на выходе генератора
с лестничной цепью обратной связи, если ![]() =
= 14,5 мА/В,
=
= 14,5 мА/В, ![]() =
2 кОм, колебательная характеристика изображена на рис. 6.17.
=
2 кОм, колебательная характеристика изображена на рис. 6.17.
Ответ: ![]() =
11,6 В.
=
11,6 В.
14. При каких условиях режим самовозбуждения автогенератора является мягким (жестким)?
15. В чем отличие мягкого режима самовозбуждения автогенератора от жесткого режима? Пояснить по графикам рис. 6.14 и рис. 6.15.
16. Каким образом объединить достоинства мягкого и жесткого режимов самовозбуждения?
Литература
1. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей: Учебник для вузов; Под ред. В.П. Бакалова. – М.: Радио и связь, 1998.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники: Учебник для вузов. – М.: Радио и связь, 1989.
3. Бакалов В.П., Крук Б.И., Журавлева О.Б. Теория электрических цепей: Учебные пособия для дистанционного обучения. – Новосибирск: СибГАТИ, 1998.
4. Krouk B.I., Zhuravleva O.B. Fundamentals of communication technique: Manual for universities and colleges. – Novosibirsk: SibSATI, 1998.
5. Крук Б.И. Методические указания к самостоятельной работе студентов над курсом ТЭЦ, часть II. Анализ линейных цепей в частотной области. – Новосибирск: НЭИС, 1989.