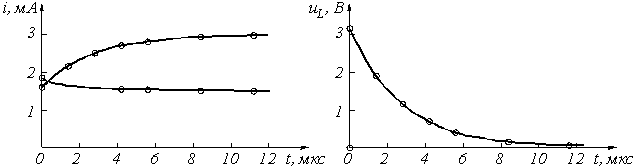Методические рекомендации по написанию, оформлению и защите контрольной работы
Контрольная работа
Задача 1
Задача 2
Контрольная работа
Задача 1
Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, конденсатор или индуктивность. В момент времени t = 0 происходит переключение ключа К, в результате чего в цепи возникает переходной процесс.
1. Перерисуйте схему цепи (см. рис. 1) для Вашего варианта (таблица 1).
2. Выпишите числовые данные для Вашего варианта (таблица 2).
3.
Рассчитайте все токи и напряжение на С или L в три
момента времени t:
![]() ,
,
![]() , ¥.
, ¥.
4.
Рассчитайте классическим методом переходный процесс в виде
![]() ,
,
![]() ,
,
![]() в схемах 1 – 5,
в схемах 1 – 5,
![]() ,
,
![]() ,
,
![]() в схемах 6 – 10. Проверьте правильность
расчетов, выполненных в п. 4, путем сопоставления их с результатами расчетов
в п. 3.
в схемах 6 – 10. Проверьте правильность
расчетов, выполненных в п. 4, путем сопоставления их с результатами расчетов
в п. 3.
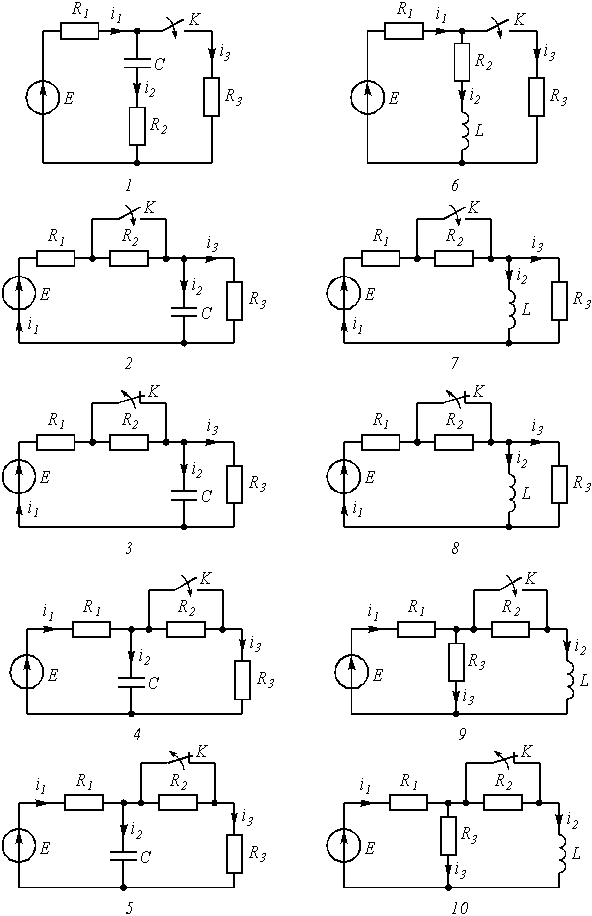
Рис. 1 |
5. Постройте графики переходных токов и напряжения, рассчитанных в п. 4. Определите длительность переходного процесса, соответствующую переходу цепи в установившееся состояние с погрешностью 5%.
6.
Рассчитайте ток
![]() операторным методом.
операторным методом.
| Варианты |
Номер схемы или задания |
|
00 10 20 30 40 50 60 70 80 90 01 11 21 31 41 51 61 71 81 91 02 12 22 32 42 52 62 72 82 92 03 13 23 33 43 53 63 73 83 93 04 14 24 34 44 54 64 74 84 94 05 15 25 35 45 55 65 75 85 95 06 16 26 36 46 56 66 76 86 96 07 17 27 37 47 57 67 77 87 97 08 18 28 38 48 58 68 78 88 98 09 19 29 39 49 59 69 79 89 99 |
1 2 3 4 5 6 7 8 9 10 |
Таблица 2
| Варианты |
С, нф или L, мГн |
|
|
|
Е, В |
|
От 00 до 09 От 10 до 19 От 20 до 29 От 30 до 39 От 40 до 49 От 50 до 59 От 60 до 69 От 70 до 79 От 80 до 89 От 90 до 99 |
20 10 10 15 15 15 20 20 15 10 |
2 1 1 1 2 1 2 2 1 0,5 |
2 1 2 1 2 2 1 1 0,5 1 |
2 1 2 2 1 1 2 1 0,5 1 |
10 5 12 12 10 10 12 12 5 5 |
Типовая задача Т1
Цепь (рис. 2 а) содержит резисторы R1 = 1 кОм, R2 = 1,5 кОм, R3 = 0,5 кОм, R4 = 2,5 кОм, индуктивность L = 6,3 мГн и источник постоянного напряжения Е = 9 В. В момент t = 0 происходит размыкание ключа К и в цепи возникает переходной процесс. Требуется: рассчитать основные характеристики процесса; получить выражения для токов i2(t), i3(t) и напряжения uL(t) классическим методов; построить графики указанных токов и напряжений; рассчитать ток i2(t) операторным методом. 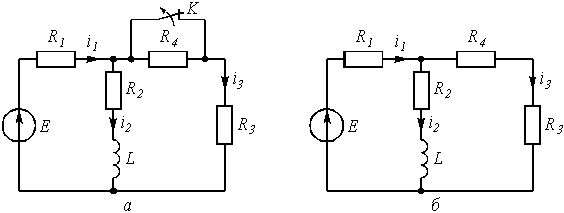
Решение
1. Находим токи i1, i2, i3 и напряжение uL в три момента времени t = 0–, 0+ и ¥.1.1. Момент t = 0–. Он соответствует стационарному состоянию цепи до коммутации. В этом состоянии резистор R4 закорочен ключом К и не влияет на работу цепи. Сама схема (рис. 2 а) представляет собой цепь, в которой uL(0–) = 0, поэтому она может быть рассчитана по следующим формулам:
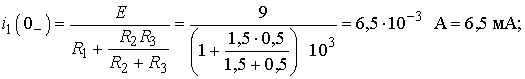
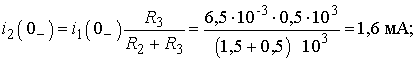
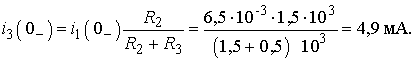
1.2. Момент t = 0+. Это первое мгновение после размыкания ключа. В соответствие с законом коммутации
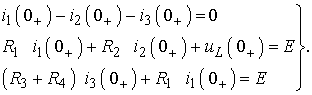
После числовых подстановок с учетом (3.1) получим:
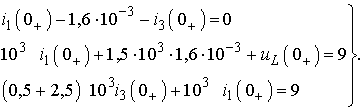
Решая систему, находим:
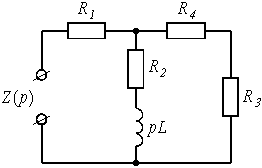
Рис. 3 |
1.3. Момент t = ¥.
Означает новое стационарное состояние цепи после окончания переходного процесса.
Внешне схема цепи при t = ¥
соответствует рис. 2 б, причем
![]() , а токи рассчитываются по формулам:
, а токи рассчитываются по формулам:
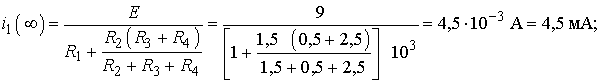
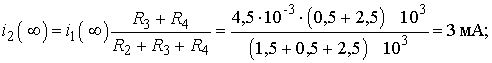
2. Расчет токов i2(t), i3(t) и напряжения uL(t) после коммутации классическим методом.
Переходный процесс в цепях первого порядка (с одним реактивным элементом) описывается уравнением вида
![]()
где fпр = f (¥) – принужденная составляющая искомой величины, равная ее значению при t = ¥; fсв(t) – свободная составляющая; A – постоянная интегрирования; р – корень характеристического уравнения, определяющий в конечном итоге длительность переходного процесса. Так как р является общей величиной для всех токов и напряжений в конкретной цепи, то расчет переходного процесса целесообразно начать с определения р.
2.1. Характеристическое уравнение для расчета р составляется по операторной схеме замещения, отражающей работу цепи после коммутации, и показанной на рис. 3.
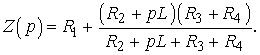
Принимая Z( p) = 0, получим характеристическое уравнение
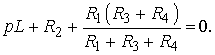
Решение уравнения дает корень
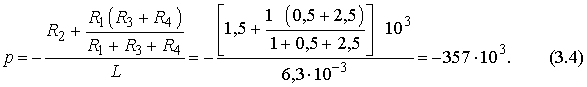
Величина
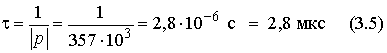
называется постоянной времени цепи.
2.2. Расчет i2(t).
В соответствии с (3.3) запишем:
Учтем, что i2пр = i2(¥) = 3 мА. Величину A1 найдем из рассмотрения i2(0+) с учетом независимого начального условия (3.1):
Откуда A1 = 1,6 – 3 = –1,4. Тогда
2.3. Расчет uL(t).
Воспользуемся законом Ома для индуктивности
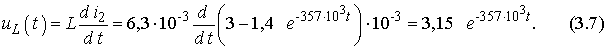
2.4. Расчет i3(t). Ведется аналогично расчету i2(t).
![]()
2.5. Проверка правильности расчетов производится путем анализа выражений (3.6), (3.7) и (3.8) в моменты времени t = 0 и ¥.
![]()
![]()
![]()
![]()
![]()
![]()
Полученные значения всех величин совпадают с результатами расчетов в п. 1.
3. Построение графиков переходного процесса.
Для построения графиков необходимо составить таблицу значений i2(t), i3(t), uL(t) в различные моменты времени (таблица 3).
| t |
0 |
0,5 t |
t |
1,5 t |
2 t |
3 t |
4 t |
|
t, мкс |
0 |
1,4 |
2,8 |
4,2 |
5,6 |
8,4 |
11,2 |
|
|
1,6 |
2,16 |
2,5 |
2,7 |
2,8 |
2,93 |
2,97 |
|
|
1,85 |
1,71 |
1,63 |
1,58 |
1,54 |
1,51 |
1,5 |
|
|
3,15 |
1,9 |
1,16 |
0,7 |
0,41 |
0,16 |
0,06 |
|
Рис. 4 |
Кривые i2(t) и i3(t) могут быть построены на одном графике. При выборе масштабных делений по осям графиков учитываются максимальные значения соответствующих величин. Для тока и напряжения целесообразно принять в 1 см по 1 мА и 1 В соответственно. Масштаб по оси времени определяется длительностью переходного процесса. Известно, что экспоненциальные функции за время t = 3t изменяется на 95% от своего максимального значения. Тогда можно принять, что переходный процесс в цепях первого порядка заканчивается через 3t с погрешностью 5%. Учитывая (3.5), получим для данной схемы tпер.пр = 3t = 8,4 мкс. Для построения графика удобно принять масштаб по оси времени 2 мкс в 1 см.
4. Расчет тока i2(t) операторным методом.
|
Рис. 5 |
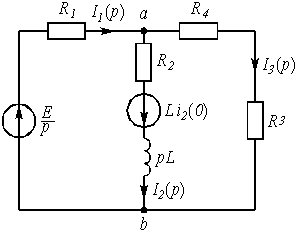
Для состояния цепи при t ³ 0 (рис. 2) составляется операторная схема замещения, которая учитывает независимые начальные условия в виде дополнительных (расчетных) источников напряжения LiL(0) или uC(0)/p. В данной задаче таким источником будет Li2(0) (рис. 5).
Используя закон Ома, в операторной форме, запишем
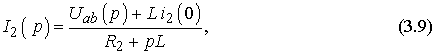
где Uab( p) может быть найдено по методу узловых напряжений:
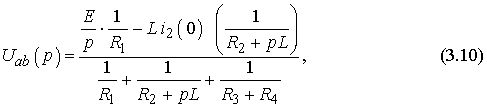
Подставляя (3.10) в (3.9), получим
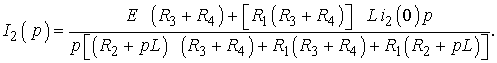
После числовых подстановок
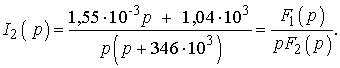
Используя теорему разложения, найдем оригинал тока:
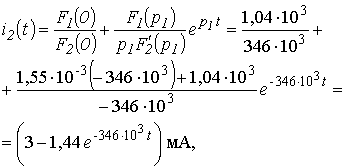
которое совпадает с выражение (3.6), полученным классическим методом.
Задача 2
Задача посвящена временному и частотному (спектральному) методам расчета реакции цепей на сигналы произвольной формы. В качестве такого сигнала используется импульс прямоугольной формы (видеоимпульс).
Электрические схемы цепей (рис.
6) содержат емкости С или индуктивности L, а также сопротивления
R. Для всех вариантов ![]() .
В схемах, где имеется сопротивление
.
В схемах, где имеется сопротивление ![]() ,
его величина
,
его величина ![]() .
Во всех схемах входным напряжением
.
Во всех схемах входным напряжением ![]() является прямоугольный импульс длительностью
является прямоугольный импульс длительностью ![]() и амплитудой
и амплитудой ![]() .
.
1. Перерисуйте схему Вашего варианта (см. табл. 1 и рис. 6). Выпишите исходные данные Вашего варианта (таблица 4).
Таблица 4
| Варианты |
С, пф или L, мкГн |
|
|
|
| От 00 до 09 От 10 до 19 От 20 до 29 От 30 до 39 От 40 до 49 От 50 до 59 От 60 до 69 От 70 до 79 От 80 до 89 От 90 до 99 |
20 25 30 20 25 30 20 25 30 25 |
1 1 1 2 2 2 3 3 3 2,5 |
30 35 40 35 40 45 35 40 45 35 |
3 4 5 6 7 3 4 5 6 7 |
Временной метод расчета
2. Рассчитайте переходную ![]() и импульсную
и импульсную ![]() характеристики цепи по напряжению классическим или операторным методами (по
выбору).
характеристики цепи по напряжению классическим или операторным методами (по
выбору).

Рис.6
3. Рассчитайте реакцию цепи в
виде выходного напряжений ![]() используя:
используя:
- интеграл Дюамеля;
- интеграл наложения.
- Постройте временные диаграммы входного и выходного напряжений.
Частотный метод расчета
5. Рассчитайте комплексные спектральные
плотности входного ![]() и выходного
и выходного ![]() сигналов.
сигналов.
6. Рассчитайте и постройте графики
модулей ![]() ,
,
![]()
![]() и модуля комплексной передаточной функции цепи
и модуля комплексной передаточной функции цепи ![]() ,
как функций от циклической частоты f в диапазоне частот 0 -
,
как функций от циклической частоты f в диапазоне частот 0 - ![]() .
.
Типовая задача Т2
Схема цепи, приведенная на рис.
7 а, содержит емкость С = 10 пф и сопротивления ![]() = 1 кОм,
= 1 кОм, ![]() = 3 кОм. На входе цепи действует прямоугольный импульс (рис. 8) длительностью
= 3 кОм. На входе цепи действует прямоугольный импульс (рис. 8) длительностью
![]() = 60 нс
и амплитудой
= 60 нс
и амплитудой ![]() = 4 В. Выполнить расчеты в соответствии с заданием к задаче 2.
= 4 В. Выполнить расчеты в соответствии с заданием к задаче 2.
Решение
1. Расчет переходной и импульсной характеристик классическим методом.
1.1. Переходная характеристика
цепи рассчитывается, как переходной процесс в виде тока или напряжения, вызванный
включением цепи с нулевыми начальными условиями на постоянное напряжение 1
В. В соответствие с этим составляется схема включения (рис. 7 б)
, на которой E = 1 В. В задаче определяется переходная характеристика
![]() по напряжению
относительно выходного контура
по напряжению
относительно выходного контура ![]() ,
поэтому можно записать, что:
,
поэтому можно записать, что:
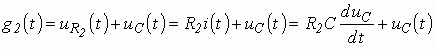 ,
(3.11)
,
(3.11)
Напряжение ![]() в схеме на рис. 3.7 б может быть рассчитано с помощью общей формулы
(3.3) расчета переходных процессов в схемах первого порядка:
в схеме на рис. 3.7 б может быть рассчитано с помощью общей формулы
(3.3) расчета переходных процессов в схемах первого порядка:
![]() ,
,
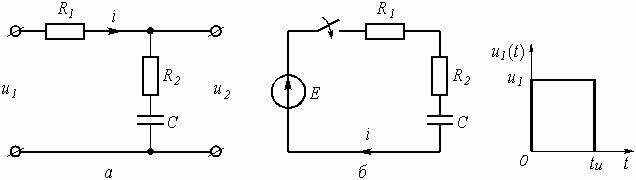
Рис.7
где ![]() = 1 В; р – корень характеристического уравнения, находится из операторного
сопротивления схемы
= 1 В; р – корень характеристического уравнения, находится из операторного
сопротивления схемы ![]() ,
и равен
,
и равен ![]() ;
постоянная интегрирования находится из рассмотрения
;
постоянная интегрирования находится из рассмотрения ![]() при
при ![]() :
:
![]() (нулевое начальное условие).
(нулевое начальное условие).
Откуда ![]() .
Окончательно
.
Окончательно
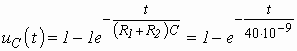 ,
,
где ![]() – постоянная времени цепи.
– постоянная времени цепи.
Подставляя ![]() в (3.11), получим:
в (3.11), получим:
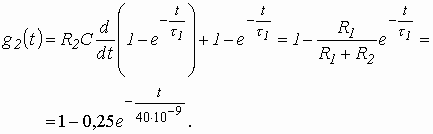 (3.12)
(3.12)
Обратить внимание, что ![]() в (3.12) определяется только элементами цепи и не зависит ни от токов, ни
от напряжений.
в (3.12) определяется только элементами цепи и не зависит ни от токов, ни
от напряжений.
1.2 Импульсная характеристика цепи h(t) есть производная от переходной характеристики h(t) = g¢ (t). Однако следует учесть, что, если переходная характеристика отлична от нуля при t = 0, т.е. имеет скачок при t = 0, то при дифференцировании появляется дополнительное слагаемое:
h(t) = g(0)d (t) + g¢ (t).
В рассматриваемой задаче ![]() = 0,75, поэтому
= 0,75, поэтому
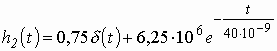 ,
(3.13)
,
(3.13)
где d (t) – импульсная функция (функция Дирака).
2. Расчет выходного напряжения
![]() временным
методов.
временным
методов.
2.1. Использование интеграла Дюамеля.
Из известных четырех формул интеграла Дюамеля наиболее общий характер имеет формула вида
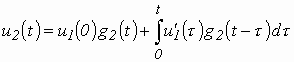 (3.14)
(3.14)
в обозначениях величин и понятий,
принятых в рассматриваемой задаче. Переменной интегрирования в (3.14) является
t (не путать с постоянной времени ![]() ).
).
Входное напряжение ![]() имеет форму прямоугольного импульса (рис. 3.8), аналитическая запись
которого может быть представлена как
имеет форму прямоугольного импульса (рис. 3.8), аналитическая запись
которого может быть представлена как
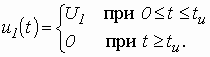 (3.15)
(3.15)
Из (3.15) следует, что ![]() и что производная
и что производная ![]() = 0 или для переменной
= 0 или для переменной ![]() = 0.
= 0.
Число участников интегрирования
в (3.14) определяется числом участков в функции, описывающей входной сигнал,
в которых она непрерывна и дифференцируема [1, с. 188]. Для функции (3.15)
таких участков в виде интервалов времени два: ![]() и
и ![]() . Необходимость
учета второго участка, когда
. Необходимость
учета второго участка, когда ![]() ,
объясняется тем, что за время действия импульса в реактивных элементах цепи
накапливается энергия электрического и магнитного полей, которая после окончания
импульса постепенно убывает до нуля, создавая напряжение и токи в цепи. Анализ
этих величин и проводится в интервале
,
объясняется тем, что за время действия импульса в реактивных элементах цепи
накапливается энергия электрического и магнитного полей, которая после окончания
импульса постепенно убывает до нуля, создавая напряжение и токи в цепи. Анализ
этих величин и проводится в интервале ![]() .
.
Важнейшей характерной особенностью аппарата интеграла Дюамеля является то, что при записи реакции цепи на каждом новом интервале времени наличие скачкообразного изменения входного сигнала в начальный момент рассматриваемого интервала учитывается дополнительным слагаемым вида
![]() ,
,
где D U – амплитуда скачка;
![]() – момент действия скачка.
– момент действия скачка.
Учитывая сказанное, запишем выходное напряжение цепи в соответствие с (3.14) и (3.12):
для интервала времени ![]()
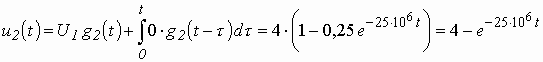 .
(3.16)
.
(3.16)
для интервала времени ![]()
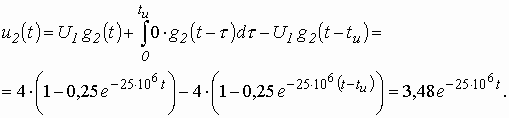 (3.17)
(3.17)
2.2. Использование интеграла наложения.
В отличие от интеграла Дюамеля в интеграле наложения не учитываются дополнительными слагаемыми скачки входного напряжения:
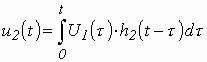 ,
(3.18)
,
(3.18)
С учетом (3.13) реакция (3.18) заданной цепи на прямоугольный импульс будет равна:
для интервала времени ![]()
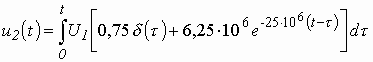 ,
,
Используя фильтрующее свойство импульсной d -функции [1. стр. 173], получим
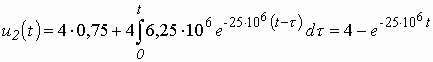 ,
,
Для интервала времени ![]()
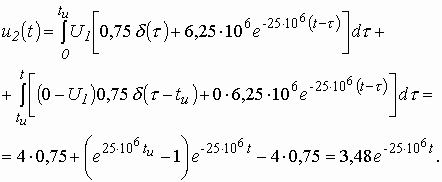
Сравнение результатов расчетов
напряжения ![]() с использованием интегралов наложения и Дюамеля показывает, что они совпадают
между собой.
с использованием интегралов наложения и Дюамеля показывает, что они совпадают
между собой.
3. Построение временной диаграммы входного и выходного напряжений.
Диаграмма выходного напряжения строится с использованием формул (3.16) и (3.17) путем подстановки в них соответствующих моментов времени. Результаты расчетов сводятся в таблицу 5.
Таблица 5
| Время, |
0 |
0,3 |
0,6 |
|
|
|
|
|
| нс |
0 |
18 |
36 |
60 |
60 |
100 |
140 |
180 |
|
|
4 |
4 |
4 |
4 |
0 |
0 |
0 |
0 |
|
|
3 |
3,4 |
3,6 |
3,8 |
0,8 |
0,28 |
0,03 |
0,01 |
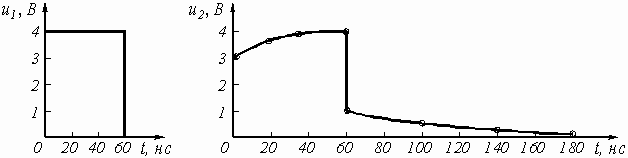
Рис.8
Из таблицы 5 видно, что ![]() в момент
в момент ![]() рассчитывается дважды: при
рассчитывается дважды: при ![]() по
формуле (3.16), а при
по
формуле (3.16), а при ![]() по формуле (3.17). Именно при такой методике можно определить будет ли скачкообразное
изменение в форме выходного сигнала в момент изменения функции, описывающей
входной сигнал, как это и показано в рассматриваемом примере.
по формуле (3.17). Именно при такой методике можно определить будет ли скачкообразное
изменение в форме выходного сигнала в момент изменения функции, описывающей
входной сигнал, как это и показано в рассматриваемом примере.
Выбор расчетных точек в интервале
![]() определяется
временем затухающего переходного процесса, которое зависит от постоянной
времени цепи, равной
определяется
временем затухающего переходного процесса, которое зависит от постоянной
времени цепи, равной ![]() = 40 нс.
= 40 нс.
Временные диаграммы входного и выходного напряжений показаны на рис. 9.
4. Расчет комплексной спектральной
плотности входного ![]() и выходного
и выходного ![]() сигналов.
сигналов.
Для расчета комплексной спектральной плотности непериодического сигнала f(t) произвольной формы используется прямое преобразование Фурье:
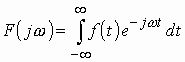 .
.
Для заданного входного сигнала (3.15) преобразование Фурье дает выражение
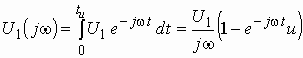 ,
,
которое после преобразований (в контрольной работе показать эти преобразования) принимает более удобную форму
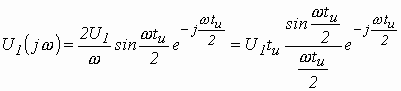 .
(3.19)
.
(3.19)
Комплексная спектральная плотность выходного сигнала находится по формуле
![]() ,
(3.20)
,
(3.20)
где ![]() – комплексная передаточная функция цепи по напряжению. Функция
– комплексная передаточная функция цепи по напряжению. Функция ![]() находится как отношение комплексного значения гармонического напряжения
находится как отношение комплексного значения гармонического напряжения
![]() на выходе
цепи к комплексному значения гармонического напряжения
на выходе
цепи к комплексному значения гармонического напряжения ![]() той же частоты, приложенному ко входу цепи:
той же частоты, приложенному ко входу цепи:
![]() .
.
Для схемы, приведенной на рис. 7 а легко получить:
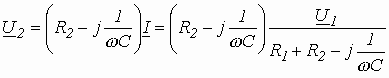 .
.
Тогда
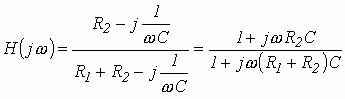 .
(3.21)
.
(3.21)
Анализ (3.21) позволяет сделать вывод, что комплексная передаточная функция цепи по напряжению определяется только элементами цепи и является безразмерной величиной.
Используя (3.19) и (3.21), находим по (3.20) спектральную плотность выходного сигнала:
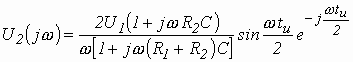 .
(3.22)
.
(3.22)
5. Расчет графиков модулей
![]() ,
, ![]() и
и ![]() .
.
Из выражений (3.19), (3.21) и (3.22) легко получить модули: спектральной плотности входного напряжения
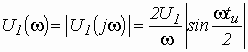 ;
(3.23)
;
(3.23)
комплексной передаточной функции (амплитудно-частотная характеристика цепи)
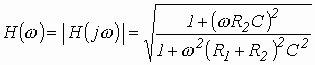 ;
(3.24)
;
(3.24)
спектральной плотности выходного напряжения
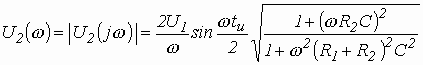 .
(3.25)
.
(3.25)
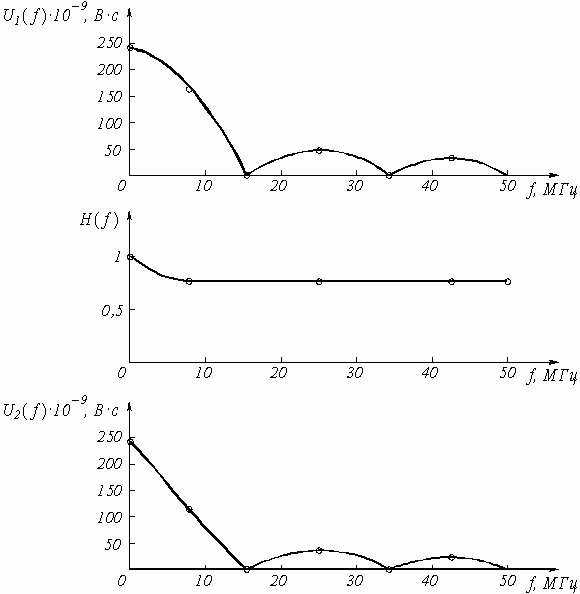
Рис.10
Для построения графиков полученных
функций необходимо выбрать расчетные точки по частоте. Учтем, что спектральная
плотность одиночного прямоугольного импульса измеряется в вольт ×
секундах [B × c] и что
она обращается в ноль на частотах ![]() и т.д. Поэтому дополнительно выбираются промежуточные точки между этими
частотами. Максимальная частота в соответствие с заданием равна 3/60 ×
10-9 = 50 × 106 Гц = 50 МГц.
Результаты расчетов по (3.23) ¸ (3.25) сводим в таблицу 6.
и т.д. Поэтому дополнительно выбираются промежуточные точки между этими
частотами. Максимальная частота в соответствие с заданием равна 3/60 ×
10-9 = 50 × 106 Гц = 50 МГц.
Результаты расчетов по (3.23) ¸ (3.25) сводим в таблицу 6.
Таблица 6
| f, МГц |
|
|
|
|
| 0 8,3 16,6 24,9 33,3 41,6 50 |
0 52,1 104,2 157 209 261 314 |
240 153 0 51 0 31 0 |
1 0,75 0,75 0,75 0,75 0,75 0,75 |
240 115 0 38 0 23 0 |
По данным таблицы 6 строим графики (рис. 10).