7 Двоичный поиск в упорядоченном массиве

1. Алгоритм двоичного поиска

1 Алгоритм двоичного поиска


Алгоритм двоичного поиска в упорядоченном массиве сводится к следующему. Берём средний элемент отсортированного массива и сравниваем с ключом X. Возможны три варианта:

    1. Выбранный элемент равен X. Поиск завершён.

    2. Выбранный элемент меньше X. Продолжаем поиск в правой половине массива.

    3. Выбранный элемент больше X. Продолжаем поиск в левой половине массива.

Далее рассмотрим две версии реализации двоичного поиска в упорядоченном массиве.

Версия 1

Пример. Найти в отсортированном массиве элемент с ключом X = б.



Рисунок 24 - Первая версия поиска

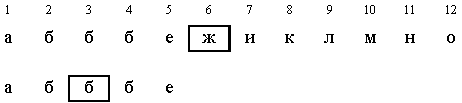
Алгоритм на псевдокоде

Поиск элемента с ключом X


Обозначим

L, R – правая и левая границы рабочей части массива.

Найден – логическая переменная, в которой будем отмечать факт успешного завершения поиска.

L: = 1, R: =n, Найден: = нет


DO (L≤R)

    m: =

    IF (am=X) Найден: =да OD FI

    IF (am < X) L: = m+1

       ELSE R: = m-1

    FI

OD


Отметим недостаток этой версии алгоритма. На каждой итерации совершается два сравнения, но можно обойтись одним сравнением. Если в массиве несколько элементов с одинаковым ключом, то эта версия находит один из них. Чтобы найти все элементы с одинаковыми ключами, необходимо просмотреть массив влево и вправо от найденного элемента.

Версия 2

Пример. Найти в отсортированном массиве элемент с ключом X = б.



Рисунок 25 - Вторая версия поиска

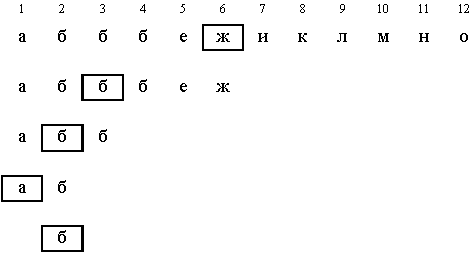
Алгоритм на псевдокоде

Поиск элемента с ключом X


L: = 1, R: =n

DO (L<R)

    m: =

    IF (am < X) L: = m+1

       ELSE R: = m

    FI

OD

IF (ar=X) Найден: =да

    ELSE Найден: =нет

FI


Нетрудно заметить, что после выхода из цикла L = R. Если в массиве несколько элементов с одинаковым ключом, то эта версия алгоритма находит самый левый из них. Для поиска остальных элементов с заданным ключом требуется просмотреть массив только в одном направлении – вправо от найденного элемента.

Дадим верхнюю оценку трудоёмкости алгоритма двоичного поиска. На каждой итерации поиска необходимо два сравнение для первой версии, одно сравнение для второй версии. Количество итераций не больше, чем . Таким образом, трудоёмкость двоичного поиска в обоих случаях

С=O(log n), n → ∞.


Контрольные вопросы

  1. Сформулируйте основную идею быстрого поиска.

  2. Чем отличаются две версии быстрого поиска друг от друга?

  3. Сравните средние трудоемкости различных версий быстрого поиска.