1 Метод прямого слияния

В основе метода прямого слияния лежит операция слияния серий. р-серией называется упорядоченная последовательность из р элементов.

Пусть имеются две упорядоченные серии a и b длины q и r соответственно. Необходимо получить упорядоченную последовательность с, которая состоит из элементов серий a и b. Сначала сравниваем первые элементы последовательностей a и b. Минимальный элемент перемещаем в последовательность с. Повторяем действия до тех пор, пока одна из последовательностей a и b не станет пустой, оставшиеся элементы из другой последовательности переносим в последовательность с. В результате получим (q+r)-серию.

Пример. Слить две серии a=(1, 4, 5, 6′) и b=(2, 3, 6″, 7, 8)

Условные обозначения | операция сравнения первых элементов списков.

Рисунок 20 - Слияние серий

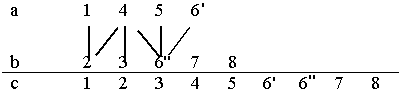
Алгоритм на псевдокоде

Слияние q – серии из списка a с r – серией из списка b, запись результата в очередь c

Слияние (a, q, b, r, c)

DO (q ≠ 0 и r ≠ 0)

   IF (a → Data ≤ b → Data)

      <Переместить элемент из списка a в очередь c>

      q:=q-1

   ELSE

      <Переместить элемент из списка b в очередь c>

      r:=r-1

   FI

OD

DO (q > 0)

   <переместить элемент из списка a в очередь c>

   q:=q-1

OD

DO (r > 0)

   <Переместить элемент из списка b в очередь c>

   r:=r-1

OD

Для алгоритма слияния серий с длинами q и r необходимое количество сравнений и перемещений оценивается следующим образом

min (q, r) ≤ C ≤ q+r-1, M=q+r

Пусть длина списка S равна степени двойки, т.е. 2^k, для некоторого натурального k. Разобьем последовательность S на два списка a и b, записывая поочередно элементы S в списки а и b. Сливаем списки a и b с образованием двойных серий, то есть одиночные элементы сливаются в упорядоченные пары, которые записываются попеременно в очереди c₀ и c₁. Переписываем очередь c₀ в список a, очередь c₁ – в список b. Вновь сливаем a и b с образованием серий длины 4 и т. д. На каждом итерации размер серий увеличивается вдвое. Сортировка заканчивается, когда длина серии превысит общее количество элементов в обоих списках. Если длина списка S не является степенью двойки, то некоторые серии в процессе сортировки могут быть короче.

Пример. Отсортировать слово методом прямого слияния.

Рисунок 21 - Метод прямого слияния

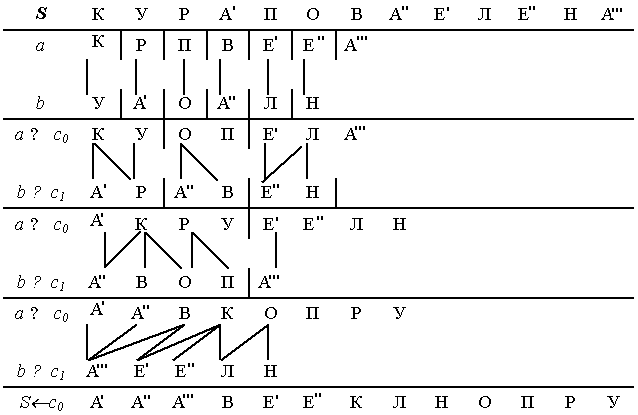
Схематически начальное расщепление последовательности S на списки a и b можно изобразить следующим образом. Ниже приведен алгоритм расщепление на псевдокоде при условии, что список S не пуст.

Рисунок 22 - Начальное расщепление

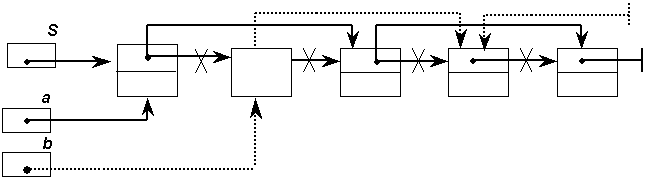
Расщепление (S, a, b, n)

Обозначим

    n - количество элементов в S

    k, p - рабочие указатели

a:=S, b:=S → Next, n:=1

k:=a, p:=b

DO (p ≠ NIL)

    n:=n+1

    k → next:=p → next

    k:=p

    p:=p → next

OD

Алгоритм на псевдокоде

Обозначим n – количество элементов в S

    a, b – рабочие списки

    c=(c₀, c₁) – массив из двух очередей

    p – предполагаемый размер серии

    q – фактический размер серии в списке a

    r – фактический размер серии в списке b

    m – текущее количество элементов в списках a и b

    i – номер активной очереди

<Расщепление (S, a, b, n)>

p:= 1

DO (p < n)

   <инициализация очередей c₀, c₁>

   i:=0, m:=n

   DO (m > 0)

      IF (m ≥ p) q:=p ELSE q:=m FI

      m:= m – q

      IF (m ≥ p) r:=p ELSE r:=m FI

      m:= m – r

      <слияние(a, q, b, r, c_i )>

      i:=1–i

   OD

   a:=c₀.Head, b:=c₁.Head

   p:=2p

OD

c₀.Tail → next:=NIL

S:=c₀.Head

При инициализации очереди обнуляются указатели, указывающие на начало и на конец очереди, т.е. очередь становится пустой.

Трудоёмкость метода прямого слияния определяется сложностью операции слияния серий. На каждой итерации происходит ровно n перемещений элементов списка и не более n сравнений. Как нетрудно видеть, количество итераций равно . Тогда

C < n, M=n+n.

Дополнительные n перемещений происходят во время начального расщепления исходного списка. Асимптотические оценки для М и С имеют следующий вид

С=О(n log n), М=О(n log n) при n → ∞.

Метод обеспечивает устойчивую сортировку. При реализации для массивов, метод требует наличия второго вспомогательного массива, равного по размеру исходному массиву. При реализации со списками дополнительной памяти не требуется.

2 Цифровая сортировка

Другим методом сортировки последовательностей является цифровая сортировка. Пусть дана последовательность из S чисел, представленных в m – ичной системе счисления. Каждое число состоит из L цифр d₁d₂…d_L, 0 ≤ d_i ≤ m – 1, i=1..L. Сначала числа из списка S распределяются по m очередям, причём номер очереди определяется последней цифрой каждого числа. Затем полученные очереди соединяются в список, для которого все действия повторяются, но распределение по очередям производится в соответствии со следующей цифрой и т.д.

Пример. Отсортировать последовательность 31 03′ 20 02 03″ 33 30 21 методом цифровой сортировки. Числа представлены в четверичной системе счисления.

Рисунок 23 - Цифровая сортировка

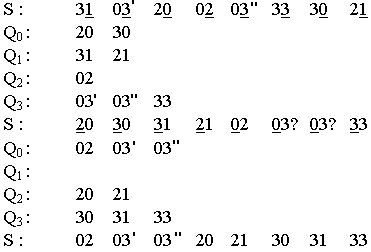
Алгоритм на псевдокоде

Цифровая сортировка

DO (j=L, L–1, … , 1)

   <инициализация очередей Q>

   <расстановка элементов из списка S в очереди Q по j – ой цифре >

   <соединение очередей Q в список S >

OD

Цифровой метод может успешно использоваться не только для сортировки чисел, но и для сортировки любой информации, представленной в памяти компьютера. Необходимо лишь рассматривать каждый байт ключа сортировки как цифру, принимающую значения от 0 до 255. Тогда для сортировки потребуется m=256 очередей. Для выделения каждого байта ключа сортировки можно использовать массив Digit, наложенный в памяти компьютера на поле элемента последовательности, по которому происходит сортировка. Приведем более детальный алгоритм цифровой сортировки.

Алгоритм на псевдокоде

Цифровая сортировка

DO (j=L, L-1, … 1)

   DO (i=0, 1, … 255)

      Q_i.Tail:=@ Q_i.Head

   OD

   p:=S

   DO (p ≠ NIL)

      d:=p → Digit[j]

      Q_d.Tail → Next:=p

      Q_d.Tail:=p

      p:=p → Next

   OD

   p:=@ S

   DO (i=0, 1, … 255)

      IF (Q_i.Tail ≠ @ Q_i.Head)

         p → Next:=Q_i.Head

         p:=Q_i.Tail

      FI

   OD

   p → Next:=NIL

OD

Для цифровой сортировки М<const L(m+n). При фиксированных m и L М=O(n) при n → ∞, что значительно быстрее остальных рассмотренных методов. Однако если длина чисел L велика, то метод может проигрывать обычным методам сортировки. Кроме того, Метод применим только, если задача сортировки сводится к задаче упорядочивания чисел, что не всегда возможно.

Метод обеспечивает устойчивую сортировку. Чтобы изменить направление сортировки на обратное, очереди нужно присоединять в обратном порядке.

Контрольные вопросы

1. В чем смысл операции слияния серий?
2. Какова сложность метода прямого слияния?
3. В чем основная идея метода цифровой сортировки?
4. Является ли метод цифровой сортировки устойчивым?
5. Можно ли применять методы сортировки последовательностей для упорядочивания массивов?