5.1 Общие сведения

Как и для представления целых чисел, для представления вещественных чисел в компьютере используется чаще всего двоичная система счисления (реже 2-16–ичная). Независимо от используемых систем счисления, существуют два типа представления чисел в компьютере: с фиксированной запятой и с плавающей запятой.

Если используется представление с фиксированной запятой, все разряды ячейки памяти служат для изображения разрядов числа (кроме знакового разряда, если он существует). При этом одному и тому же разряду числа соответствует всегда один и тот же разряд ячейки. Т.е. место запятой фиксируется около определённого разряда. Именно в таком виде представлены целые числа в компьютере. Место запятой при этом – после младшего разряда, вне разрядной сетки. Такая система записи числа упрощает выполнение арифметических операций, но сильно ограничивает диапазон представляемых чисел.

Делались попытки представить в подобном виде и вещественные числа. Чаще всего это были числа из диапазона [–1,1]. Число в компьютере предлагалось представлять, к примеру, следующим образом:

……………

Этот случай соответствует соглашению, что запятая стоит перед самым старшим разрядом, а число, соответствующее такой записи, равно

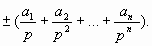
Наибольшее по абсолютной величине число, которое может быть представлено в компьютере таким образом, равно 1–р^–n, а наименьшее равно – р^–n. Поскольку реально числа бывают и больше, и меньше этого диапазона, приходилось вводить “масштабные множители”, что существенно усложняло решение задачи.

Поэтому в современных ЭВМ принят другой способ представления вещественных чисел – с плавающей запятой. Этот способ опирается на нормализованную (экспоненциальную) запись числа.

Замечание. Термин “экспонента” имеет два близких, но всё же различных значения. Первое – это функция . В математических книгах часто встречается запись exp(x) (как и в большинстве языков программирования). Второе значение экспоненты – показатель степени вообще. Например, для числа , 3 будет экспонентой. Именно в этом смысле используется буква E при записи чисел в калькуляторах и языке Паскаль:.

Нормализованная форма записи неравного нулю вещественного числа – это представление числа в виде , где q – целое число (положительное, отрицательное или ноль), m – правильная p-ичная дробь, у которой первая цифра после запятой не равна нулю:
,
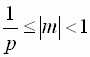p – основание системы счисления.
При этом m называют мантиссой, а q – порядком числа.

В нормализованном виде мантисса записывается в p-ичном виде, а порядок – в десятичном.

 

Пример 1. Записать в нормализованном виде.

0,0017₁₀=0,17x 10^–2, здесь m=0,17; q= –2; p=10;

100,01₂=0,10001x 2³, здесь m=0,10001; q= 3; p=2;

Следует отметить, что число ноль не может быть записано в нормализованной форме так, как она определена, поэтому его запись оговаривается отдельно: (и мантисса, и порядок равны нулю).

Нормализованной такая форма записи названа потому, что в ней все числа записываются одинаково (по единой норме), в том смысле, что запятая ставится всегда в одном и том же месте – перед самой старшей (левой) значащей цифрой.

Итак, теперь мы будем рассматривать только нормализованные числа, представленные в виде: – т.к. при представлении в компьютере используется двоичная система счисления.

Для представления вещественного числа в компьютере выделяется ячейка памяти, часть разрядов которой отводится для записи мантиссы, часть – для записи порядка, и один разряд – для записи знака числа.

Как правило, в любом языке программирования используется несколько вещественных типов, которые отличаются размером ячейки памяти, различным количеством разрядов, отведённых под мантиссу и порядок, и местом их расположения.

Таблица 6: Вещественные типы языков TP и С.

Размер в байтах	Диапазон значений	Точность	Название в ТР	Название в С
6	10-39…1038	11-12 знач. цифр	Real
4	10-45…1038	7-8 знач. цифр	single	float
8	10-324…10308	15-16 знач. цифр	double	double
10	10-4951…104932	19-20 знач. цифр	extended	long int

5.2 Схема записи вещественного нормализованного числа в ячейку памяти компьютера на примере типа Real (Turbo Pascal)

Тип real не случайно приведён в таблице 6 первым, хотя его размер не является минимальным. Дело в том, что на современных компьютерах для работы с вещественными числами используются сопроцессоры (раньше их ставили дополнительно, а сейчас они встроены в процессор). А процессор работает только с целыми числами.

Так вот, первые компиляторы для языка TP разрабатывались тогда, когда персональные компьютеры сопроцессоров не имели, а система команд процессора содержала операции лишь над целыми числами (и по сей день тип real не использует сопроцессоры). Реализацию арифметических операций над вещественными числами разработчики вынуждены были проводить самостоятельно. Поэтому схема записи числа такого типа отличается от других вещественных типов, которые являются сопроцессорными.

Как следует из таблицы, под каждую переменную типа real отводится 6 байт памяти. Распределены они следующим образом: старший разряд – под знак числа, младшие 8 разрядов – под запись порядка, остальные – под запись мантиссы. Схема записи такого числа изображена на рисунке (k_m, k_q –количество разрядов, отведённых под мантиссу и под порядок):

47	46		8	7		0
знак мантиссы	m km = 39 разрядов			q + t kq = 8 разрядов

Т.к. в двоичной системе счисления в нормализованной форме после запятой всегда стоит 1, число всегда в виде: , то эту “старшую” единицу в типе real не записывают в мантиссу. Т.е m здесь – мантисса без старшей единицы. При арифметических операциях эта единица восстанавливается.

Знак числа записывается так: 0 – положительное число; 1 – отрицательное. Знак мантиссы есть знак всего числа.

Однако и порядок числа может быть как отрицательным, так и положительным целым числом. При представлении целых чисел для записи отрицательных величин использовался дополнительный код. Но в записи вещественных чисел он не используется.

Порядок числа записывается в специальном виде q+t, где q – собственно порядок, а t – сдвиг (смещение) порядка.

Сдвиг вычисляется по формуле:

Если под запись порядка, как в данном случае, выделено 8 разрядов (k_q=8), то сдвиг будет .

Сдвиг порядка используется для того, что бы порядок всегда представлялся в виде положительного беззнакового числа и все восемь нулей в записи порядка со сдвигом соответствовали минимальному возможному порядку (а не q = 0).

Действительно, если t = 128, и в разрядах, отведённых под порядок со сдвигом, записано 8 нулей: 0000 0000. Чему тогда равен порядок?

q+t = 0000 0000₂ = 0. q = –t = –128. Это будет минимальный возможный порядок для данной ячейки.

Если в разрядах, отведённых под порядок со сдвигом, все единицы:

1111 1111₂ =255 255 = q+t q = 255 – 128 = 127. Это будет максимальный возможный порядок для данной ячейки.

Наоборот, если порядок q = 0, что будет записано в соответствующих разрядах?

q+t = 0 + 128 Там будет записано 1000 0000.

В общем, можно сделать вывод: если реальный порядок отрицательный, то в старшем из этих 8-ми разрядов будет 0, а если не отрицательный (), то там стоит 1( наоборот со знаком мантиссы).

А смысл введения сдвига порядка был следующий: при таком представлении упрощалась операция сравнения числа с нулём, которая аппаратно выполняется довольно часто.

Таким образом, любое число типа real имеет следующий нормализованный вид:

, где , .

 

Пример 2. В ячейке, отведённой под число типа real, все разряды заняты нулями. Что это за число?

0

000 . . . 0

0 0000000

 

Т.к. в знаковом разряде стоит 0, это число положительное. Его мантисса равна 0,1 (т.к. при записи в ячейку памяти старшую единицу не писали, но теперь мы её восстанавливаем). Найдём порядок: q + t = 0 q = –t = –128. Т.е. это число:

(т.е. получили очень маленькое, но всё же не равное нулю, как можно было подумать, число). Получили машинный ноль.

Минимальное представимое в данном типе число называется машинным нулём.

Пример 3. Что за число записано в ячейке памяти, если все разряды, кроме знакового, заняты нулями?

1

000 . . . 0

0 0000000

 

Т.к. в знаковом разряде стоит 1, это число отрицательное; все остальные рассуждения аналогичны примеру 2. Т.е. записанное число равно – это “минус ноль”.

Т.е. машинных нуля два : один +0, другой –0.

Таким образом представить “просто ноль” в типе real нельзя, т.к. в мантиссе всегда неявно присутствует единица.

Т.к. для записи мантиссы отведено определённое количество разрядов, то возможны случаи, когда все цифры мантиссы в эти разряды не помещаются. Тогда число округляется по следующему правилу: если надо округлить до k-го разряда (включительно), то смотрят k+1 разряд. Если там ноль – просто отбрасывают оставшуюся часть, если там 1 – эту единицу прибавляют к k-му разряду.

 

Пример 4. Примеры округления до 5-го разряда двоичных чисел:

1) 0,100111111 т.к. в 6-м разряде стоит 1, прибавляем к 5-му разряду 1:

0,10011+0,00001 =0,10100 – после округления.

2) 0,100110111 т.к. в 6-м разряде стоит 0, отбрасываем все значащие цифры после 5-го разряда: 0,10011– после округления.

 

Пример 5.Записать в ячейку памяти типа REAL число 12,25₁₀. Переведём число в двоичную систему и нормализуем:

12,25₁₀=1100,01₂=0,110001×2⁴;

Вычислим порядок со сдвигом: q=4 (порядок), 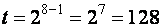(сдвиг).

q+t=4+128=132₁₀=10000100₂.

Т.к. число положительное, в знаковый разряд пишем ноль, затем идёт мантисса без старшей единицы и порядок со сдвигом:

 

0

100010000 . . .

10000100

 

Вычислим границы диапазона типа Real. Запишем в ячейку памяти максимально возможное по абсолютной величине число (в знаковом разряде 0, в остальных 1). Чему равно такое число?

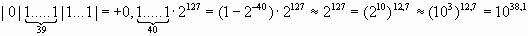
А минимальное по модулю число мы уже нашли – это машинный ноль, который .

Таким образом, диапазон чисел, представимых в типе real:

().

Этот диапазон говорит лишь о величине представимых чисел, но не о точности представления. Это вовсе не значит, что мы можем в типе real представить число, состоящее из 38 десятичных цифр. Во-первых, десятичное число, даже имеющее всего одну значащую цифру после запятой, вообще говоря, невозможно записать точно в любом из вещественных типов. Подробнее этот вопрос мы обсудим в пункте 5.4. Во-вторых, на точность представления чисел влияет размер мантиссы. В данном случае мантисса может состоять из 40-значащих двоичных цифр (39 записываются явно, а одна подразумевается). Это позволяет записать число, состоящее из 40 единиц, которое равно . Это и даёт 10-12 значащих цифр, указанных в таблице 6.

5.3 Сопроцессорные вещественные типы языка TP.

Как уже было сказано, в современных компьютерах с вещественными числами работает не процессор, а сопроцессор. Чтобы обеспечить в своих системах поддержку сопроцессорных типов, Borland вводит в Turbo Pascal типы Single (4 байта), Double (8 байт) и Extended (10 байт). Extended – это родной для сопроцессора тип, а типы Single и Double получаются из него очень простым усечением. При загрузке числа типа Single или Double во внутренний регистр сопроцессора последний конвертирует их в Extended. Напротив, при выгрузке чисел этих типов из регистра в память сопроцессор усекает их до нужного размера. Внутренние же операции всегда выполняются с данными типа Extended.

При представлении этих чисел в компьютере мантисса и порядок меняются местами, оставляя неизменным расположение знакового разряда:

знак

q+t –порядок со сдвигом

мантисса(m)

В сопроцессорных типах порядок так же представляется с использованием сдвига. Но в этих типах данных (в extended всегда, а в остальных только в случае, когда q + t =0) число предварительно преобразовывается к виду:

, где ,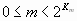

и сдвиг вычисляется по формуле . Найдём минимально и максимально возможный порядок:

q + t = 0 (min) q = –t ()

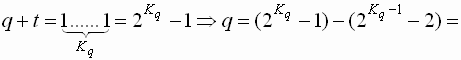
Т.е.

Т.о. в этих типах минимальная ненулевая мантисса состоит из n–1 нуля после запятой и одной самой правой единицы:

0

0 .. ..0

00… .. 01

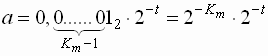
Отсюда и возникает несимметричность в допустимом диапазоне значений (на него теперь влияем не только порядок, но и мантисса).

Пример 6 . Найдём минимальное представимое число для типа single (4 байта). В этом типе .

.

Соответственно, минимальное представимое число будет:

5.4 Арифметические операции.

При выполнении арифметических операций над числами, представленными в формате с плавающей запятой, надо отдельно выполнять операции для мантисс и порядков. Но сначала числа нормализуются!

 

1. Порядки чисел а и b выравниваются по большему из них (пусть, для определённости, это будет число a). Для этого мантисса числа b сдвигается вправо на соответствующее количество разрядов (часть значащих цифр при этом может оказаться утерянной).
2. Выполняется операция сложения (вычитания) над мантиссами с округлением по значению (k+1) –ой значащей цифры результата;
3. Мантисса результата нормализуется, поэтому получившийся порядок может измениться как в меньшую, так и в большую сторону.

Пример 7. Пусть длина мантиссы 8 разрядов. Вычислим разность чисел и . Сначала оба числа нормализуем:

.

Выполним вычитание мантисс:

_0,10000

  0,00011

  0,01101

Результат a-b=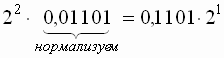

Рассмотрим теперь ошибки, которые могут возникнуть при операциях сложения и вычитания.

1. Потеря значащих цифр мантиссы у меньшего из чисел при выравнивании порядков.

Пример 8 . Пусть длина мантиссы 8 разрядов. Вычислить сумму чисел:

и .







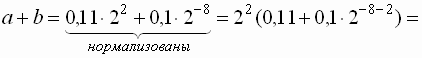
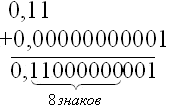
Поскольку длина мантиссы 8 разрядов, то последние цифры будут отброшены при округлении, в результате получим a + b = a (что в обычной математике не бывает, если ).

2. Потеря значащих цифр мантиссы результата при вычитании близких по модулю чисел.

Пример 9. Пусть длина мантиссы 8 разрядов. Вычислить разность чисел и .

а) Сначала произведём вычисления вне зависимости от разрядности мантиссы:



 

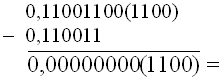
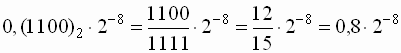= =0,003125₁₀.

Это точный “теоретический” результат.

б) теперь вычислим a–b c учётом разрядности мантиссы:

число a будет записано как: 0,110011001100(1100). После округления до 8-ми разрядов, а=0,11001101, и



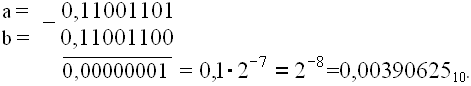
Сравним с ранее полученным результатом. Уже вторая значащая цифра оказалась неверной.

3. Выход за границу допустимого диапазона значений типа при нормализации результата.

В данном случае получаемый порядок оказывается либо больше максимально возможного значения, либо меньше минимального:

 

Пример 10 .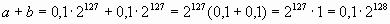

Если числа a и b являются переменными типа real, то результат окажется непредставимым в данном типе. Такую ситуацию разные компиляторы обрабатывают по-разному, чаще всего выдаётся сообщение об ошибке: “арифметическое переполнение”.

 

1. Мантиссы перемножаются (или делятся), результат округляется до k  значащих цифр (предварительно выравнивать порядки не требуется).
2. Порядки при умножении складываются, а при делении вычитаются.
3. При необходимости мантисса результата нормализуется.

Пример 11. Найти axb, a : b, если a=0, 001101₂, b=100,1₂, длина мантиссы 8 разрядов.

Нормализуем числа:

a=0,1101x 2^–2, b=0,1001x 2³ .

1) ax b=(0,1101x 2^–2)´ (0,1001x 2³)=(0,1101 x 0,1001) x 2^–2+3=0,1110101x2 (округлять и нормализовать нет необходимости).

2) a : b=(0,1101x 2^–2): (0,1001x 2³) =(0,1101 : 0,1001) x 2^–2–3=

=1,01110000111….x2^–5= нормализуем =0,101110000111….x 2^–4 = округляем по 8-ой разряд = 0, 10111000x 2^–4.

При умножении и делении, так же как и при сложении, возможно возникновение арифметического переполнения, или получение машинного нуля вместо достаточно малого, но не равного нулю числа.

Замечание. При выполнении промежуточных вычислений или при сдвиге порядка у одного из чисел мантисса записывается в отведённыё разряды полностью (включая старшую единицу после запятой). Старшая единица мантиссы не хранится только у результата после нормализации.

Выполнение арифметических операций с вещественными числами требует проведения нормализации, что приводит к изменению порядков. Этим и объясняется термин “плавающая запятая”, т.е. запятая “плавает” с места на место.

Пример 12. Рассмотрим, как будет выглядеть запись мантиссы (m) числа а=при различных значениях – количества разрядов, отведённых под мантиссу. Сначала переведём число в двоичный вид с указанием периода и нормализуем:

а=– нормализовали.

1) Пусть “Запишем” мантиссу в это количество разрядов, округлив до соответствующего знака:

.

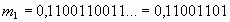Теперь “восстановим” это число:

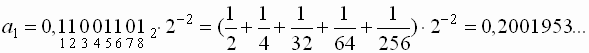
2) Пусть 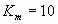. Вновь запишем мантиссу:

. (округлили)

Теперь “восстановим”:

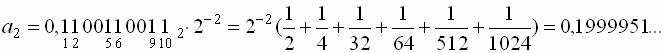
Сравним полученные результаты. Вспомним, что записывали в память число 0,2. В первом случае получили приближение числа с избытком, во втором – с недостатком. Но точно исходное число мы записать не сможем. Это объясняется тем, что конечные десятичные дроби часто оказываются бесконечными периодическими двоичными дробями. Значит, в нормализованном виде число будет иметь бесконечную мантиссу, которую придётся округлить при записи в конечное число разрядов.

 

Пример 13. Вопрос, что напечатает программа после запуска?

var R1:single: R2:double;

begin

    R1:=0.2;

    R2:=0.2:

    if R1=R2 then writeln(‘Равно’)

                    else writeln(‘Неравно’);

end.

 

Т.к. число 0.2 не представимо в виде конечной десятичной дроби (как мы выяснили, дробь периодическая), в зависимости от типа переменной мантисса будет округлена до разного количества десятичных знаков, следовательно, они не будут равны.

 

Пример 14. Задача – написать на языке Pascal  программу, вычисляющую значения функции f(x)=x² на отрезке [0,1] с шагом 0,2. Типичная для начинающих программистов программа выглядит следующим образом:

var a:real;

begin         a:=0.0;

                   while a<>1 do

                   begin

                            writeln(‘a=’,a,’ f(a)=’, sqr(a));

                            a:=a+0.2;

end;

end.

Т.к. число 0.2 точно в компьютере не представимо, следовательно, если к 0.0 пять раз прибавить 0.2, ровно 1 не получится (будет число либо чуть-чуть меньше 1, либо чуть-чуть больше). И программа «зациклится».

 

Итог.

1. Уже на этапе записи чисел в компьютер возникают ошибки округления, которые нарастают при выполнении арифметических операций.
2. В результате вычитания могут возникнуть ненадёжные значащие цифры.
3. Добавление или вычитание очень малого числа может никак не сказаться на результате.
4. Получение очень больших чисел может вызвать переполнение порядка, а очень малого – появление нуля (что может вызвать аварийную остановку программы).
5. Некорректно сравнивать в программе вещественные числа на точное равенство.

Вопросы и задачи для самопроверки

1. Записать в нормализованном виде числа 0,0017₁₀; 100,01₂; 1043,24₅.
2. Записать в k разрядов мантиссу числа 0,3₁₀ при k=8,10. Результаты перевести в десятичную с.с., округлив при этом до 5 знаков, и сравнить с точным значением.
3. Вычислить сумму и разность чисел а и b, используя компьютерный алгоритм сложения и вычитания: а = 10₂ и b = 0,011₂.
4. Вычислить сумму чисел а = 0,0000000001 и b=110, если под мантиссу отведено 8 разрядов, используя компьютерный алгоритм сложения.
5. Вычислить, используя компьютерный алгоритм вычитания, а – b, а=0,1(011); b=0,1011 сначала без учета разрядности мантиссы, затем при 8-ми отведенных под мантиссу разрядах. Мантиссу разности перевести в десятичную с.с.
6. Вычислить, используя компьютерный алгоритм умножения, 101,1_{2 ´} 1010₂.
7. Вычислить, используя компьютерный алгоритм деления, 1101110₂ : 1011₂.
8. Пусть для представления числа отведены следующие разряды: k_m= 8 бит, k_q=4 бита, 1 бит под знак. При этом расположение разрядов как в типе REAL, и старшая единица также не пишется в мантиссу. Найти: 1) сдвиг порядка; 2) машинный ноль; 3) максимальное положительное число; 4) число 1111111110000.
9. Пусть k_m=8 бит, k_q= 4 бита; а= 0,111111₂; b= 111,1₂ × 2^-9. При этом расположение разрядов как в типе REAL, и старшая единица также не пишется в мантиссу. Вычислить a+b, используя “компьютерный” алгоритм. Сравнить результат с точным значением. Записать вычисленный результат в отведенные биты.