Практические задания
Молекулярная физика. Термодинамика
Физика атомов и атомного ядра. Элементарные частицы. Основы квантовой механики. Физика твердого тела
Молекулярная физика. Термодинамика
Основные формулы
Количество вещества однородного газа (в молях)
или 
,
где N – число молекул газа;
- постоянная Авогадро; m
– масса газа; M – молярная масса газа.
Если система представляет смесь нескольких газов, то количество вещества системы
или
где 
- соответственно количества вещества, число молекул, масса, молекулярная масса
i-й компоненты смеси.
Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа):
где m – масса газа; М
– молярная масса газа; R – молярная газовая постоянная; 
- количество вещества; Т – термодинамическая температура.
а) закон Бойля – Мариотта (изотермический процесс – Т =const, m=const):
или для двух состояний газа:
б) закон Гей-Люссака (изобарный процесс – p =const, m =const):
или для двух состояний:
в) закон Шарля (изохорный процесс – V =const, m =const):
или для двух состояний:
г) объединенный газовый закон (m =const):
или 
где 
- давление, объем и температура газа в начальном состоянии; 
- те же величины в конечном состоянии.
Закон Дальтона, определяющий давление смеси газов:
где 
- парциальные давления компонентов смеси; n – число компонентов смеси.
Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.
Молярная масса смеси газов:
где 
- масса i-го компонента смеси; 
- количество вещества i-го компонента смеси; n – число компонентов
смеси.
Массовая доля 
,
где m – масса смеси.
Концентрация молекул:
где N – число молекул,
содержащихся в данной системе; 
- плотность вещества, V – объем системы. Формула справедлива не
только для газов, но и для любого агрегатного состояния вещества.
Основное уравнение кинетической теории газов:
,
где 
- средняя кинетическая энергия поступательного движения молекулы.
Средняя кинетическая энергия поступательного движения молекулы:
где k – постоянная Больцмана.
Средняя полная кинетическая энергия молекулы:
где i – число степеней свободы молекулы.
Зависимость давления газа от концентрации молекул и температуры:
Скорости молекул:
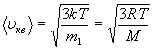(средняя
квадратичная);
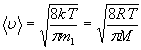(средняя
арифметическая);
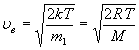(наиболее
вероятная),
где 
- масса одной молекулы.
Относительная скорость молекулы:
где 
- скорость данной молекулы.
Удельные теплоемкости газа при
постоянном объеме 
и при постоянном давлении 
:
Связь между удельной с и молярной С теплоемкостями:
Уравнение Майера:
Внутренняя энергия идеального газа:
Первое начало термодинамики:
где Q – теплота, сообщенная
системе (газу); 
- изменение внутренней энергии системы; А – работа, совершенная системой
против внешних сил.
Работа расширения газа:
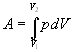(в
общем случае);
(при
изобарном процессе);
(при
изотермическом процессе);
или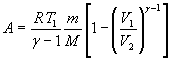 
(при адиабатном процессе),
где 
-
показатель адиабаты.
Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:
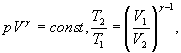
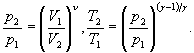
Термический к.п.д. цикла:
где 
теплота, полученная рабочим телом от теплоотдатчика; 
теплота переданная рабочим телом теплоприемнику.
Термический к.п.д. цикла Карно:
где 
и 
термодинамические
температуры теплоотдатчика и теплоприемника.
Коэффициент поверхности натяжения:
или 
где F – сила поверхностного
натяжения, действующая на контур l ограничивающий поверхность жидкости;
изменение свободной энергии поверхностной
пленки жидкости, связанной с изменением площади 
поверхности этой пленки.
Формула Лапласа, выражающая давление р, создаваемое сферической поверхностью жидкости:
где R – радиус сферической поверхности.
Высота подъема жидкости в капиллярной трубке:
где 
краевой
угол (
при полном
смачивании стенок трубки жидкостью; 
при полном несмачивании); R – радиус канала трубки; p – плотность
жидкости; g – ускорение свободного падения.
Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями:
где d – расстояние между плоскостями.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 1. Определить число N молекул,
содержащихся в объеме 
воды, и массу 
молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся
друг с другом, найти диаметр d молекул.
РЕШЕНИЕ. Число N молекул,
содержащихся в некоторой системе массой m, равно произведению постоянного
Авогадро 
на
количество вещества v:
.
Так как 
где
M – молярная масса, то 
Выразив в этой формуле массу как произведение плотности на объем V, получим:
Произведем вычисления, учитывая,
что 
(см. прил.,
табл. 14):
Массу 
одной молекулы можно найти по формуле
(2)
Поставив в (2) значения M
и 
, найдем массу
молекулы воды:
Если молекулы воды плотно прилегают
друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая
ячейка) 
, где
d - диаметр молекулы. Отсюда
(3)
Объем 
найдем, разделив молярный объем 
на число молекул в моле, т.е. на 
:
.
(4)
Подставим выражение (4) в (3):
где 
Тогда
(5)
Проверим, дает ли правая часть выражения (5) единицу длины:
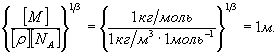
Произведем вычисления:
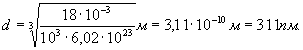
ПРИМЕР 2. В болоне объемом
V=10 л находится гелий под давлением 
и при температуре 
После того как из баллона было взято m = 10 г гелия, температура в баллоне понизилась
до 
Определить
давление 
гелия,
оставшегося в баллоне.
РЕШЕНИЕ. Для решения задачи воспользуемся уравнением Менделеева – Клапейрона, применив его к конечному состоянию газа:
(1)
где 
масса гелия в баллоне в конечном состоянии; М – молярная масса гелия;
R – молярная газовая постоянная.
Из уравнения (1) выразим искомое давление:
(2)
Массу 
гелия выразим через массу 
,
соответствующую начальному состоянию, и массу m гелия, взятого из баллона:
(3)
Массу 
гелия найдем также из уравнения Менделеева – Клапейрона, применив его к начальному
состоянию:
(4)
Подставив выражение массы 
в (3), а затем выражение 
в (2), найдем
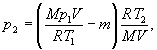
или
(5)
Проверим, дает ли формула (5)
единицу давления. Для этого в ее правую часть вместо символов величин подставим
их единицы. В правой части формулы два слагаемых. Очевидно, что первое из них
дает единицу давления, так как состоит из двух множителей, первый из которых
безразмерный,
а второй – давление. Проверим второе слагаемое:
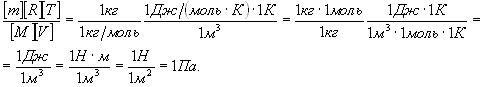
Паскаль является единицей давления.
Произведем вычисления по формуле (5), учитывая, что 
(см. прим., табл. 14):
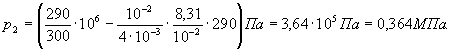
ПРИМЕР 3. Баллон содержит
кислорода
и 
аргона.
Давление смеси р=1МПа, температура Т=300К. Принимая данные газы за идеальные,
определить объем V баллона.
РЕШЕНИЕ. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси.
По уравнению Менделеева – Клапейрона
парциальные давления 
кислорода
и 
аргона выражаются формулами:
Следовательно, по закону Дальтона давление смеси газов
или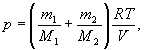 
откуда объем баллона
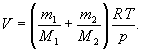(1)
Произведем вычисления, учитывая,
что 
(см. прил.,
табл. 14):
ПРИМЕР 4. Найти среднюю
кинетическую энергию 
вращательного движения одной молекулы кислорода при температуре Т=350К, а также
кинетическую энергию 
вращательного движения всех молекул кислорода массой m = 4г.
РЕШЕНИЕ. На каждую степень
свободы молекулы газа приходится одинаковая средняя энергия, 
где к – постоянная Больцмана; Т – термодинамическая температура
газа. Так как вращательному движению двухатомной молекулы (молекула кислорода
– двухатомная) соответствуют две степени свободы, то средняя энергия вращательного
движения молекулы кислорода
(1)
Кинетическая энергия вращательно движения всех молекул газа
(2)
Число всех молекул газа
(3)
где 
постоянная Авогадро; v – количество вещества.
Если учесть, что количество
вещества 
где
m – масса газа; М – молярная масса газа, то формула (3) принимает
вид
Подставив выражение N в формулу (2), получаем
(4)
Произведем вычисления, учитывая,
что для кислорода 
(см. прил., табл. 14):
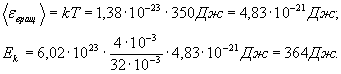
ПРИМЕР 5. Вычислить удельные
теплоемкости при постоянном объеме 
и при постоянном давлении 
неона и водорода, принимая эти газы за идеальные.
РЕШЕНИЕ. Удельные теплоемкости идеальных газов выражаются формулами:
(1) 
(2)
где i – число степеней свободы
молекулы газа; М – молярная масса. Для неона (одноатомный газ) i
=3 и 
(см. прил.,
табл. 14).
Произведем вычисления:
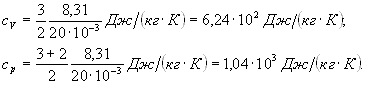
Для водорода (двухмерный газ)
i =5 и 
.
Тогда:
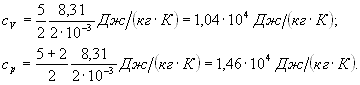
ПРИМЕР 6. Вычислить удельные
теплоемкости 
и 
смеси неона
и водорода, если массовые доли неона и водорода составляют, 
и 
Значения удельных
теплоемкостей газов взять из предыдущего примера.
РЕШЕНИЕ. Удельную теплоемкость
смеси
при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания
смеси на 
, выразим двумя способами:
(1)
(2)
где 
удельная
теплоемкость неона; 
удельная
теплоемкость водорода.
Приравняв правые части (1)
и (2) и разделив обе части полученного равенства на ,
получим 
откуда
(3)
или
(4)
где 
и 
.
Рассуждая так же, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:
(5)
Произведем вычисления:
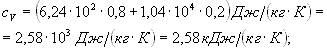
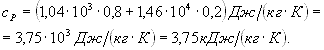
ПРИМЕР 7. Кислород массой
m=2 кг занимает объем 
и находится под давлением 
Газ был нагрет сначала при постоянном давлении до объема 
а
затем при постоянном объеме до давления 
Найти изменение 
внутренней энергии газа, совершенную им работу А и теплоту Q,, переданную газу.
Построить график процесса.
РЕШЕНИЕ. Изменение внутренней энергии газа
(1)
где i – число степеней свободы
молекул газа (для двухатомных молекул кислорода i = 5), 
разность температур газа в конечном (третьем) и начальном состояниях.
Начальную и конечную температуру
газа найдем из уравнения Менделеева – Клапейрона 
откуда
Работа расширения газа при постоянном давлении выражается формулой
Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е.
Следовательно, полная работа, совершаемая газом,
Согласно первому началу термодинамики
теплота Q, переданная газу, равна сумме изменения внутренней энергии 
и работы А:
Произведем вычисления, учтя,
что для кислорода 
(см. прил., табл. 14):
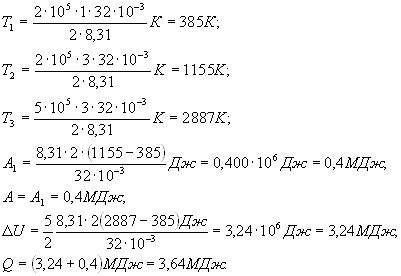
График процесса приведен на рис. 8.
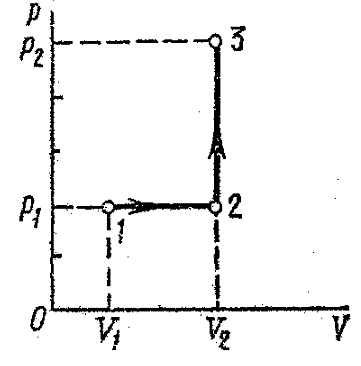
Рис.8
ПРИМЕР 8. В цилиндре под
поршнем находится водород массой m=0,02кг при температуре, 
Водород сначала расширился адиабатно, увеличив свой объем в 
раз, а затем был сжат изотермически, причем объем газа уменьшился в 
раз. Найти температуру в конце адиабатного расширения и работу, совершенную
газом при этих процессах. Изобразить процесс графически.
РЕШЕНИЕ. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением
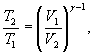или 
где 
отношение
теплоемкостей газа при постоянном давлении и постоянном объеме, 
Отсюда получаем следующее выражение для конечной температуры:
Работа 
газа при адиабатном расширении может быть определена по формуле
где 
молярная
теплоемкость газа при постоянном объеме. Работа 
газа при изотермическом процессе может быть выражена в виде
или 
где 
Произведем вычисления, учтя,
что для водорода как двухатомного газа 
и 
Так как 
(находится логарифмированием), то
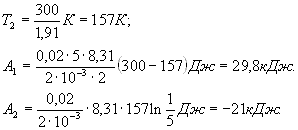
Знак “минус” показывает, что при сжатии работа газа совершается над газом внешними силами. График процесса приведен на рис. 9.
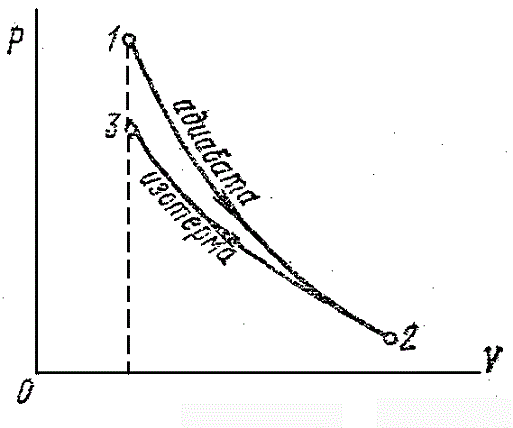
Рис.9
ПРИМЕР 9. Тепловая машина
работает по обратимому циклу Карно. Температура теплоотдатчика 
.
Определить термический к. п. д. 
цикла
и температуру 
теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной
от теплоотдатчика, машина совершает работу 
.
РЕШЕНИЕ. Термический к. п. д. тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Термический к. п. д. выражается формулой
,
где 
теплота,
полученная от теплоотдатчика; А – работа, совершенная рабочим теплом
тепловой машины.
Зная к. п. д. цикла, можно
по формуле 
определить температуру охладителя 
:
.
Произведем вычисления:
ПРИМЕР 10. Найти добавочное
давление внутри мыльного пузыря диаметром 
.
Какую работу нужно совершить, чтобы выдуть этот пузырь?
РЕШЕНИЕ. Пленка мыльного пузыря имеет две сферические поверхности – внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенный внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обеих поверхностей практически одинаковы. Поэтому добавочное давление
,
где r – радиус пузыря. Так
как 
, то
.
Работа, которую нужно совершить,
чтобы, растягивая пленку, увеличить ее поверхность на 
,
выражается формулой
или 
.
В данном случае 
общая
площадь двух сферических поверхностей пленки мыльного пузыря; 
общая
площадь двух поверхностей плоской пленки, затягивавшей отверстие трубки до выдувания
пузыря. Пренебрегая 
,
получаем
.
Произведем вычисления:
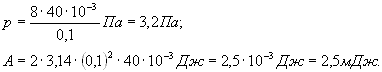
Оптика
Основные формулы
Скорость света в среде:
,
где с – скорость света в вакууме; n – показатель преломления среды.
Оптическая длина пути световой волны:
,
где l – геометрическая длина пути световой волны в среде с показателем преломления n.
Оптическая разность хода двух световых волн:
.
Зависимость разности фаз от оптической разности хода световых волн:
,
где 
- длина световой волны.
Условие максимального усиления света при интерференции:
.
Условие максимального ослабления света:
.
Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки:
или
,
где d – толщина пленки; n – показатель преломления пленки; 
угол
падения; 
угол
преломления света в пленке.
Радиус светлых колец Ньютона в отраженном свете:
(к=1,2,3,…),
где к – номер кольца; R – радиус кривизны.
Радиус темных колец Ньютона в отраженном свете:
.
Угол 
отклонения лучей, соответствующей максимуму (светлая полоса) при дифракции
на одной щели, определяется из условия
(к=0,1,2,3,…),
где а – ширина щели; к – порядковый номер максимума.
Угол
отклонения лучей, соответствующей максимуму (светлая полоса) при дифракции
света на дифракционной решетке, определяется из условия
(к=0,1,2,3,…),
где d – период дифракционной решетки.
Разрешающая способность дифракционной решетки:
,
где 
наименьшая
разность длин волн двух соседних спектральных линий (
и 
), при которой
эти линии могут быть видны раздельно в спектре, полученном посредством данной
решетки; N – полное число щелей решетки.
Формула Вульфа-Брэггов:
,
где 
угол
скольжения (угол между направлением параллельного пучка рентгеновского излучения,
падающего на кристалл, и атомной плоскостью в кристалле; d – расстояние
между атомными плоскостями кристалла.
Закон Брюстера:
,
где 
угол
падения, при котором отразившийся от диэлектрика луч полностью поляризован;
относительный
показатель преломления второй среды относительно первой.
Закон Малюса:
,
где 
интенсивность
плоскополяризованного света, падающего на анализатор; I – интенсивность этого
света после анализатора; 
угол
между направлением колебаний электрического вектора света, падающего на анализатор,
и плоскостью пропускания анализатора (если колебания электрического вектора
падающего света совпадают с этой плоскостью, то анализатор пропускает данный
свет без ослабления).
Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:
а) 
(в твердых телах),
где 
постоянная
вращения; d – длина пути, пройденного светом в оптически активном веществе;
б) 
(в растворах),
где 
удельное
вращение; 
массовая
концентрация оптически активного вещества в растворе.
Релятивистская масса:
,
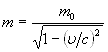или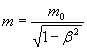 
,
где 
масса
покоя частицы; 
ее
скорость; с – скорость света в вакууме; 
скорость
частицы, выраженная в долях скорости света 
.
Взаимосвязь массы и энергии релятивистской частицы:
,
или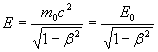 
,
где 
энергия
покоя частицы.
Полная энергия свободной частицы:
,
где Т – кинетическая энергия релятивистской частицы:
Кинетическая энергия релятивистской частицы:
,
или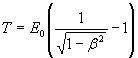 
.
Импульс релятивистской частицы:
,
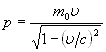или 
.
Связь между полной энергией и импульсом релятивистской частицы:
.
Закон Стефана-Больцмана:
,
где 
энергетическая
светимость (излучательность) абсолютно черного тела; 
постоянная
Стефана-Больцмана; Т – термодинамическая температура Кельвина.
Закон смещения Вина:
,
где 
длина
волны, на которую приходится максимум энергии излучения; b – постоянная
Вина.
Энергия фотона:
,
или 
,
где h – постоянная Планка;
постоянная Планка, деленная
на 
; v
– частота фотона; 
циклическая
частота.
Масса фотона:
,
где с – скорость света в
вакууме; 
длина
волны фотона.
Импульс фотона:
.
Формула Эйнштейна для фотоэффекта:
,
где 
энергия
фотона, падающего на поверхность металла; А – работа выхода электрона;
максимальная
кинетическая энергия фотоэлектрона.
Красная граница фотоэффекта:
,
или 
,
где 
минимальная
частота света, при которой еще возможен фотоэффект; 
максимальная
длинна волны света, при которой еще возможен фотоэффект; h – постоянная
Планка; с – скорость света в вакууме.
Формула Комптона:
,
или
,
где 
длина
волны фотона, встретившегося со свободным или слабо связанным электроном; 
длина
волны фотона, рассеянного на угол 
после столкновения с электроном; 
масса
покоящегося электрона.
Комптоновская длина волны:
.
Давление света при нормальном падении на поверхность:
,
где 
энергетическая
освещенность (облученность); 
объемная
плотность энергии излучения; 
коэффициент
отражения.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 1. От двух когерентных
источников 
и 
(
)
лучи попадают на экран. На экране наблюдается интерференционная картина. Когда
на пути одного из лучей перпендикулярно ему поместили мыльную пленку (n=1,33),
интерференционная картина изменилась на противоположную. При какой наименьшей
толщине 
пленки
это возможно?
РЕШЕНИЕ. Изменение интерференционной картины на противоположную означает, что на тех участках экрана, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционной картины возможен при изменении оптической разности хода пучков световых волн на нечетное число половин длин волн, т. е.
,
(1)
где 
оптическая разность хода пучков световых волн до внесения пленки; 
оптическая
разность хода тех же пучков после внесения пленки: 
Наименьшей толщине 
пленки соответствует к=0. При этом формула (1) примет вид
.
(2)
Выразим оптические разности
хода 
и 
.
Из рис. 32. следует:
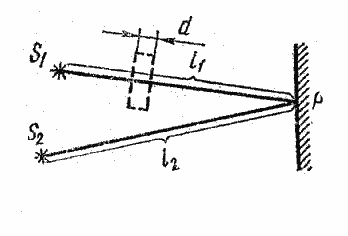
Рис.32
.
Подставим выражение
и в формулу
(2): 
, или
.2. Отсюда
.
Произведем вычисления:
.
ПРИМЕР 2. На стеклянный
клин с малым углом нормально к его грани падает параллельный пучок лучей монохроматического
света с длинной волны 
.
Число т возникающих при этом интерференционных полос, приходящихся на l см,
равно 10. Определить угол 
клина.
РЕШЕНИЕ. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти отраженные пучки света когерентны. Поэтому на поверхности клина будут наблюдаться интерференционные полосы. Так как угол клина мал, то отраженные пучки 1 и 2 света (рис. 33) будут практически параллельны.
Темные полосы видны на тех участках клина, для которых разность хода лучей кратна нечетному числу половин длин волн:
.
(1)
Разность хода 
двух волн складывается из разности оптических длин путей этих волн 
и половины длины волны 
. Величина
представляет собой добавочную
разность хода, возникающую при отражении световой волны 1 от оптически
более плотной среды. Подставляя в формулу (1) разность хода 
световых волн, получаем
,
(2)
где n – показатель преломления
стекла 
; 
толщина
клина в том месте, где наблюдается темная полоса, соответствующая номеру 
угол
преломления.
Согласно условию угол падения
равен нулю, следовательно, и угол преломления 
равен нулю, а 
.
Раскрыв скобки в правой части равенства (2), после упрощения получаем
.
(3)
Пусть произвольной темной полосе
к-го номера соответствует толщина 
клина, а темной полосе 
-го
номера – толщина 
клина. Тогда на рис. 33, учитывая, что m полос укладывается на расстоянии
l, найдем
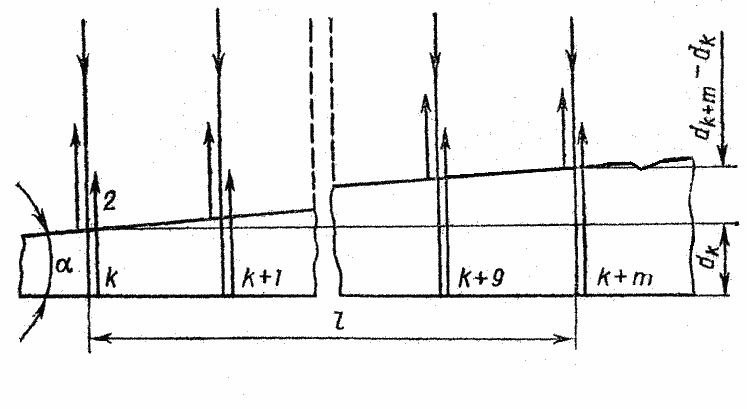
Рис.33
.
(4)
Выразим из (3)
и и подставим
их в формулу (4). Затем, учитывая, что 
(из-за малости угла 
),
получим
.
Подставляя значения физических величин, найдем
.
Выразим 
в градусах. Для этого можно воспользоваться соотношением между радианом и секундой:
,
т.е.
.
ПРИМЕР 3. На дифракционную
решетку в направлении нормали к ее поверхности падает монохроматический свет.
Период решетки 
. Определить
наибольший порядок дифракционного максимума, который дает эта решетка в случае
красного 
и
в случае фиолетового 
света.
РЕШЕНИЕ. Из формулы, определяющей положение главных максимумов дифракционной решетки, найдем порядок m дифракционного максимума:
,
(1)
где d – период решетки;
угол дифракции;
длина волны
монохроматического света. Так как 
не может быть больше 1, то число m не может быть больше 
,
т. е.
.
(2)
Подставив в формулу (2) значения, получаем:
(для красных лучей);
(для фиолетовых лучей).
Если учесть, что порядок максимумов
является целым числом, то для красного света 
и для фиолетового 
.
ПРИМЕР 4. Пучок естественного
света падает на полированную поверхность стеклянной пластины, погруженной в
жидкость. Отраженный от пластины пучок света образует угол 
с падающим пучком (рис. 34). Определить показатель преломления 
жидкости, если отраженный свет максимально поляризован.
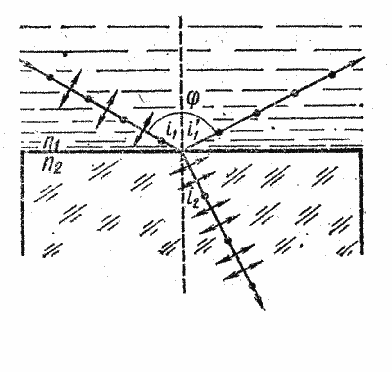
Рис.34
РЕШЕНИЕ. Согласно закону Брюстера
пучок света, отраженный от диэлектрика, максимально поляризован в том случае,
если тангенс угла падения численно равен относительному показателю преломления
, где 
показатель
преломления второй среды (стекла) относительно первый (жидкости).
Относительный показатель преломления
равен отношению абсолютных показателей преломления. Следовательно, 
.
Так как угол падения равен
углу отражения, то 
и, следовательно, 
,
откуда
.
Произведем вычисления:
.
ПРИМЕР 5. Два николя 
и 
расположены
так, что угол между их плоскостями пропускания составляет 
.
Определить, во сколько раз уменьшится интенсивность 
естественного света: 1) при прохождении через один николь ;
2) при прохождении через оба николя. Коэффициент поглощения света в николе 
.
Потери на отражение света не учитывать.
РЕШЕНИЕ 1. Естественный свет, падая на грань призмы Николя (рис. 35), расщепляется вследствие двойного лучепреломления на два пучка: обыкновенный и необыкновенный.
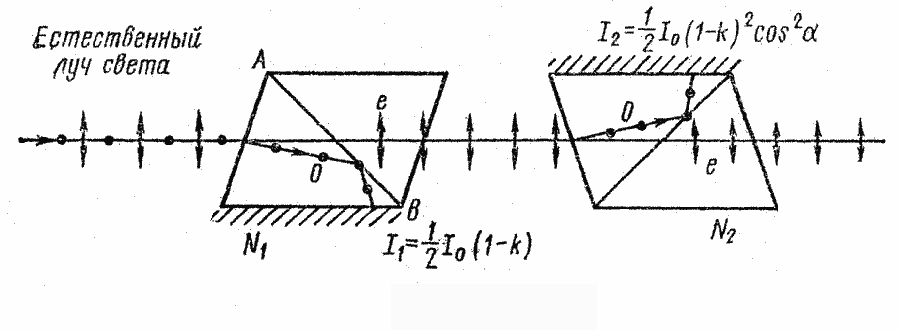
Рис.35
Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний обыкновенного пучка перпендикулярна плоскости чертежа. Обыкновенный пучок света (0) вследствие полного отражения от границы АВ отбрасывает на зачерненную поверхность призмы и поглощается ею. Необыкновенный пучок (е) проходит через призму, уменьшая свою интенсивность вследствие поглощения. Таким образом, интенсивность света, проходящего через первую призму,
.
Относительное уменьшение интенсивности
света получим, разделив интенсивность 
естественного света, падающего на первый николь, на интенсивность 
поляризованного света:
.
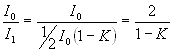(1)
Произведем вычисления:
.
(2)
Таким образом, интенсивность уменьшается в 2,1 раза.
2. Плоскополяризованный пучок
света интенсивности
падает на второй николь
и также расщепляется на два пучка различной интенсивности: обыкновенный и необыкновенный.
Обыкновенный пучок полностью поглощается призмой, поэтому интенсивность его,
нас не интересует. Интенсивность 
необыкновенного пучка, вышедшего из призмы ,
определяется законом Малюса (без учета поглощения света во втором николе):
,
где 
угол
между плоскостью колебаний в поляризованном пучке и плоскостью пропускания николя
.
Учитывая потери интенсивности на поглощение во втором николе, получаем
.
Искомое уменьшение интенсивности
при прохождении света через оба николя найдем, разделив интенсивность
естественного света на интенсивность
света, прошедшего систему из двух николей:
.
Заменяя отношение 
его выражением по формуле (1), получаем
.
Произведем вычисления:
.
ПРИМЕР 6. Плоскополяризованный
монохроматический пучок света падает на поляроид и полностью им гасится. Когда
на пути пучка поместили кварцевую пластину, интенсивность I пучка света после
поляроида стала равна половине интенсивности пучка, падающего на поляроид. Определить
минимальную толщину кварцевой пластины. Поглощением и отражением света поляроид
пренебречь, постоянную вращения 
кварца принять равной 
.
РЕШЕНИЕ. Полное гашение света поляроидом означает, что плоскость пропускания поляроида (пунктирная линия на рис. 36) перпендикулярна плоскости колебаний (I-I) плоскополяризованного света, падающего на него. Введение кварцевой пластины приводит к повороту плоскости колебаний света на угол
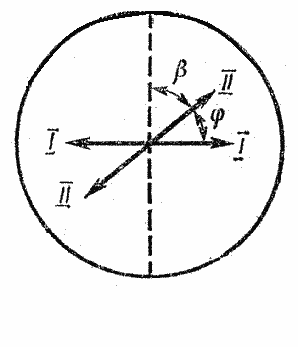
Рис.36
,
(1)
где 
толщина
пластины.
Зная, во сколько раз уменьшиться
интенсивность света при прохождении его через поляроид, определим угол 
,
который установится между плоскостью пропускания поляроида и новым направлением
(II-II) плоскости колебаний падающего на поляроид плоскополяризованного света.
Для этого воспользуемся законом Малюса:
.
Заметив, что 
,
можно написать 
,
или
.
(2)
Из равенства (2) с учетом (1)
получаем 
,
откуда искомая толщина пластины
.
Произведем вычисления во внесистемных единицах:
.
ПРИМЕР 7. Определить импульс
p и кинетическую энергию Т электрона, движущегося со скоростью 
,
где с – скорость света в вакууме.
РЕШЕНИЕ. Импульсом частицы называется произведение массы частицы на ее скорость:
.
(1)
Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле
,
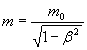(2)
где m – масса движущейся
частицы; 
масса
покоящейся частицы; 
-
скорость частицы, выраженная в долях скорости света.
Заменив в формуле (1) массу
m ее выражении (2) и приняв во внимание, что 
,
получим выражение для релятивистского импульса:
.
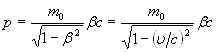(3)
Произведем вычисления:
.
В релятивистской механике кинетическая
энергия Т частицы определяется как разность между полной энергией Е
и энергией покоя 
этой частицы, т. е. 
.
Так как 
и 
,
то учитывая зависимость массы от скорости, получаем
,
или
.
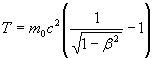Произведем вычисления:
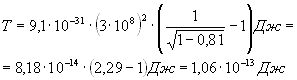
Так как во внесистемных единицах
, то вычисления
упрощаются:
.
ПРИМЕР 8. Определить релятивистский импульс электрона, обладающего кинетической энергией Т=5МэВ.
РЕШЕНИЕ. Решение задачи сводиться к установлению соотношения между релятивистским импульсом р частицы и ее кинетической энергией Т.
Сначала установим связь между релятивистским импульсом и полной энергией частицы. Полная энергия Е частицы прямо пропорциональна ее массе, т. е.
.
(1)
Зависимость массы от скорости определяется формулой
.
(2)
Заменив массу m в формуле
(1) ее выражением (2) и приняв во внимание, что 
,
получим
.
(3)
Возведя обе части равенства (3)
в квадрат, найдем 
,
откуда
.
(4)
Очевидно, что
.
Поэтому равенство (4) можно
переписать в виде 
,
откуда релятивистский импульс
.
Разность между полной энергией
и энергией покоя есть кинетическая энергия Т частицы: 
.
Легко убедиться, что 
,
поэтому искомая связь между импульсом и энергией релятивистской частицы выразим
формулой
.
Вычисления удобно провести в два приема: сначала найти числовое значение радикала во внесистемных единицах, а затем перейти к вычислению в единицах СИ. Таким образом,
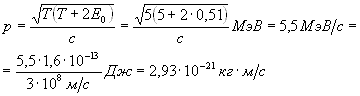
ПРИМЕР 9. Длина волны, на
которую приходится максимум энергии в спектре излучения абсолютно черного тела,
. Определить
энергетическую светимость (излучательность)
поверхности тела.
РЕШЕНИЕ. Энергетическая светимость
абсолютно
черного тела в соответствии с законом Стефана-Больцмана пропорциональна четвертой
степени термодинамической температуры и выражается формулой
,
(1)
где 
постоянная
Стефана-Больцмана; Т – термодинамическая температура.
Температуру Т можно выразить с помощью закона смещения Вина:
,
(2)
где b – постоянная закона смещения Вина.
Используя формулы (2) и (1), получаем
(3)
Произведем вычисления:
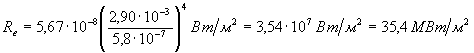
ПРИМЕР 10. Определить максимальную
скорость 
фотоэлектронов,
вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны
; 2) 
излучением
с длиной волны 
.
РЕШЕНИЕ. Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта:
,
(1)
где 
энергия
фотонов, падающих на поверхность металла; А – работа выхода; 
максимальная
кинетическая энергия фотоэлектронов.
Энергия фотона вычисляется также по формуле
,
(2)
где h – постоянная Планка;
с – скорость света в вакууме; 
длина
волны.
Кинетическая энергия электрона может быть выражена или по классической формуле
,
(3)
или по релятивистской формуле
(4)
в зависимости от того, какая скорость
сообщается фотоэлектрону. Скорость фотоэлектрона зависит от энергии фотона,
вызывающего фотоэффект: если энергия 
фотона много меньше энергии покоя 
электрона, то может быть применена формула (3), если же
сравнима по величине с ,
то вычисления по формуле (3) приводят к ошибке, поэтому нужно пользоваться формулой
(4).
1. Вычислим энергию фотона ультрафиолетового излучения по формуле (2):
,
или
Полученная энергия фотона (8эВ) много меньше энергии покоя электрона (0,51МэВ). Следовательно, для данного случая кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (3):
,
откуда
.
(5)
Проверим, дает ли полученная формула единицу скорости. Для этого в правую часть формулы (5) вместо символов величин подставим обозначения единиц:
.
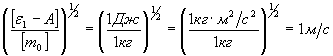Найденная единица является единицей скорости.
Подставив значения величин в формулу (5), найдем
.
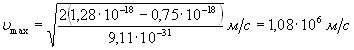2. Вычислим энергию фотона 
излучения
,
или во внесистемных единицах:
.
Работа выхода электрона (А=4,7эВ)
пренебрежимо мала по сравнению с энергией фотона (
),
поэтому можно принять, что максимальная кинетическая энергия электрона равна
энергии фотона: 
.
Так как в данном случае кинетическая энергия электрона больше его энергия покоя,
то для вычисления скорости электрона следует взять релятивистскую формулу кинетической
энергии (4). Из этой формулы найдем
.
Заметив, что 
и 
, получим
.
Произведем вычисления:
.
ПРИМЕР 11. В результате
эффекта Комптона фотон при соударении с электроном был рассеян на угол 
.
Энергия рассеянного фотона 
.
Определить энергию фотона 
до рассеяния.
РЕШЕНИЕ. Для определения энергии первичного фотона воспользуемся формулой Комптона:
,
(1)
где 
изменение
длины волны фотона в результате рассеяния на свободном электроне; h –
постоянная Планка; 
масса
покоя электрона; с – скорость света в вакууме; 
угол
рассеяния фотона.
Преобразуем формулу (1): 1)
заменим в ней 
на 
; 2) выразим
длины волн 
и 
через энергии
и 
соответствующих фотонов, воспользовавшись формулой 
;
3) умножим числитель, и знаменатель правой части формулы на с. Тогда
.
Сократим на hc и выразим из этой формулы искомую энергию:
,
(2)
где 
энергия
покоя электрона.
Вычисления по формуле (2) удобнее
вести во внесистемных единицах. Так как для электрона 
,
то
.
ПРИМЕР 12. Пучок монохроматического
света с длиной волны 
падает нормально на зеркальную плоскую поверхность. Поток излучения 
.
Определить: 1) силу давления F, испытываемую этой поверхностью; 2)число фотонов
, ежесекундно
падающих на поверхность.
РЕШЕНИЕ 1. Сила светового давления на поверхность равна произведению светового давления p на площадь S поверхности:
.
(1)
Световое давление может быть найдено по формуле
,
(2)
где 
-
энергетическая освещенность (облученность); с – скорость света в вакууме;
коэффициент
отражения.
Подставляя правую часть выражения (2) в формулу (1), получаем
.
(3)
Поскольку 
представляет собой поток излучения 
,
то
.
(4)
Произведем вычисления, учитывая,
что для зеркальной поверхности 
:
.
2. Произведение энергии 
одного фотона на число фотонов 
,
ежесекундно падающих на поверхность, равно мощности излучения, т. е. потоку
излучения: 
,
а так как энергия фотона 
,
то
,
откуда
.
(5)
Произведем вычисления:
.
Физика атомов и атомного ядра. Элементарные частицы. Основы квантовой механики. Физика твердого тела
Основные формулы
Боровская теория
Момент импульса электрона (второй постулат Бора)
,
или 
,
где m – масса электрона:
скорость электрона
на n-й орбите; 
радиус
n-й стационарной орбиты; 
постоянная
Планка; n – главное квантовое число (n=1,2,…).
Радиус n-й стационарной орбиты:
,
где 
радиус
Бора.
Энергия электрона в атоме водорода:
,
где 
энергия
ионизации атома водорода.
Энергия, излучаемая или поглощаемая атомом водорода:
,
или
,
где 
и 
- квантовые
числа, соответствующие энергетическим уровням, между которыми совершается переход
электрона в атоме.
Спектроскопическое волновое число:
,
где 
длина
волны изучения или поглощения атомом; R – постоянная Ридберга.
Волновые свойства частиц
Длина волны де Бройля:
,
где p – импульс частицы.
Импульс частицы и его связь с кинетической энергией Т:
а) 
;
б)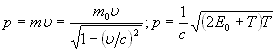 
.
где 
масса
покоя частицы; m – релятивистская масса; 
скорость
частицы; с – скорость света в вакууме; 
энергия
покоя частицы (
).
Соотношение неопределенностей:
а) 
(для координаты и импульса);
где 
неопределенность
проекции импульса на ось х; 
неопределенность
координаты;
б) 
(для энергии и времени),
где 
неопределенность
энергии; 
время
жизни квантовой системы в данном энергетическом состоянии.
Одномерное уравнение Шредингера для стационарных состояний:
,
где 
волновая
функция, описывающая состояние частицы; m – масса частицы; Е –
полная энергия; 
потенциальная
энергия частицы.
Плотность вероятности:
,
где 
вероятность
того, что частица может быть обнаружена вблизи точки с координатой х
на участке dx.
Вероятность обнаружения частицы
в интервале от 
до 
:
.
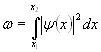Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:
а) 
(собственная нормированная волновая функция);
б) 
(собственное значение энергии),
где n – квантовое число (n=1,2,3,…); l – ширина ящика.
В области 
и 
.
Пространственная решетка кристалла:
Молярный объем кристалла:
,
где М – молярная масса;
плотность кристалла.
Объем элементарной ячейки для решетки кубической сингонии:
,
где а – параметр решетки.
Число элементарных ячеек в одном моле кристалла:
;
если кристалл состоит из одинаковых атомов, то
,
где n – число одинаковых
атомов, приходящихся на элементарную ячейку; 
постоянная
Авогадро.
Отношение числа элементарных ячеек к объему кристалла:
;
если кристалл состоит из одинаковых атомов, то
.
Параметр кубической решетки из одинаковых атомов:
.
Расстояние между соседними атомами в кубической решетке:
а) 
(гранецентрированной);
б) 
(объемно – центрированной).
Теплоемкость кристалла
Средняя энергия квантового одномерного осциллятора:
,
где 
нулевая
энергия (
);
постоянная Планка; 
круговая
частота колебаний осциллятора; к – постоянная Больцмана; Т – термодинамическая
температура.
Молярная внутренняя энергия системы, состоящей из невзаимодействующих квантовых осцилляторов:
,
где R – молярная газовая
постоянная; 
характеристическая
температура Эйнштейна; 
молярная
нулевая энергия (по Эйнштейну).
Молярная теплоемкость кристаллического твердого тела по Дебаю:
,
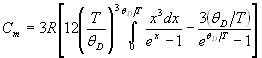где 
характеристическая
температура Дебая (
).
Молярная теплоемкость кристаллического твердого тела в области низких температур (предельный закон Дебая)
.
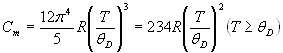Теплота, необходимая для нагревания тела:
,
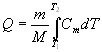где m – масса тела; М
– молярная масса; 
и 
начальная
и конечная температура тела.
Элементы квантовой статистики
Распределение свободных электронов в металле по энергиям при 0 К:
,
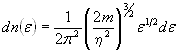где 
концентрация
электронов, энергии которых заключены в пределах от 
до 
; m
– масса электрона. Это выражение справедливо при 
(где 
энергия
или уровень Ферми).
Энергия Ферми в металле при Т=0 К
,
где n – концентрация электронов в металле.
Полупроводники
Удельная проводимость собственных полупроводников:
,
где е – элементарный заряд;
n – концентрация носителей заряда (электронов и дырок); 
и 
- подвижности
электронов и дырок.
Напряжение на гранях прямоугольного образца при эффекте Холла, холловская разность потенциалов:
,
где 
постоянная
Холла; В – магнитная индукция; j – плотность тока; а –
ширина пластины (образца).
Постоянная Холла для полупроводников типа алмаз, германий, кремний и др., обладающих носителями заряда одного вида (n или р):
,
где n – концентрация носителей заряда.
Магнетики
Связь магнитной индукции В с напряженностью Н магнитного поля в изотропном магнетике:
,
где 
магнитная
проницаемость среды; 
магнитная
постоянная.
Намагниченность однородного изотропного магнетика:
,
где 
магнитный
момент i-й молекулы (атома); N – число молекул в объеме V.
Молярная намагниченность однородного изотропного магнетика:
,
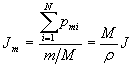где m – масса магнетика;
М – молярная масса; 
плотность
магнетика.
Удельная намагниченность однородного изотропного магнетика:
,
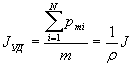Магнитная восприимчивость однородного изотропного магнетика:
,
где Н – напряженность магнитного поля.
Молярная магнитная восприимчивость однородного изотропного магнетика:
.
Удельная магнитная восприимчивость однородного изотропного магнетика:
.
Связь магнитной восприимчивости с магнитной проницаемостью:
.
Намагниченность при насыщении в случае однородного изотропного магнетика:
,
где n – концентрация молекул
атомов с магнитным моментом 
.
Магнитная восприимчивость парамагнитного
однородного изотропного магнетика при условии 
:
,
где к – постоянная Больцмана; Т – термодинамическая температура.
Магнетон Бора:
.
где 
масса
электрона; 
.
Частота прецессии Лармора:
.
где В – магнитная индукция.
Атомное ядро. Радиоактивность
Массовое число ядра (число нуклонов в ядре):
,
где Z – зарядовое число (число протонов); N – число нейтронов.
Закон радиоактивного распада:
,
или 
,
где dN – число ядер, распадающихся
за интервал времени dt; N – число ядер, нераспавшихся к моменту
времени t; 
число
ядер в начальный момент (t=0); 
постоянная
радиоактивного распада.
Число ядер, распавшихся за время t:
.
В случае если интервал времени
, за который
определяется число распавшихся ядер, много меньше периода полураспада 
,
то число распавшихся ядер можно определить по формуле
.
Зависимость периода полураспада от постоянной радиоактивного распада:
.
Среднее время 
жизни радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся
ядер уменьшается в е раз:
.
Число N атомов, содержащихся в радиоактивном изотопе:
,
где m – масса изотопа; М
– молярная масса; 
постоянная
Авогадро.
Активность А радиоактивного изотопа:
,
или 
.
где dN – число ядер, распадающихся
за интервал времени dt; 
активность
изотопа в начальный момент времени.
Удельная активность изотопа:
.
Дефект массы ядра:
,
где Z – зарядовое число
(число протонов в ядре); А – массовое число (число нуклонов в ядре);
число нейтронов
в ядре; 
масса
протона; 
масса
нейтрона; 
масса
ядра.
Энергия связи ядра:
,
где 
дефект
массы ядра; с – скорость света в вакууме.
Во внесистемных единицах энергия
связи ядра 
,
где дефект массы 
в а. е. м.; 931 – коэффициент пропорциональности (1 а. е. м. ~ 931 МэВ).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 1. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.
РЕШЕНИЕ. Для определения энергии фотона воспользуемся сериальной формулой для водородоподобных ионов:
,
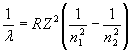(1)
где λ – длина волны фотона; R
– постоянная Ридберга; Z – заряд ядра в относительных единицах (при 
формула переходит в сериальную формулу для водорода); 
номер
орбиты, на которую перешел электрон; 
номер
орбиты, с которой перешел электрон (
и 
главные квантовые
числа).
Энергия фотона 
выражается формулой
.
Поэтому, умножив обе части равенства (1) на hc, получим выражение для энергии фотона:
.
Так как Rhc есть энергия
ионизации 
атома
водорода, то
.
Вычисления выполним во внесистемных
единицах: 
(см.
прил., табл.1); 
.
ПРИМЕР 2. Электрон, начальной
скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов
U. Найти длину волны де Бройля λ для двух случаев: 1) 
;
2) 
.
РЕШЕНИЕ. Длина волны де Бройля для частицы зависит от ее импульса р и определяется формулой
,
(1)
где h – постоянная Планка.
Импульс частицы можно определить, если известна ее кинетическая энергия Т. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).
В нерелятивистском случае
,
(2)
где 
масса
покоя частицы.
В релятивистском случае
,
(3)
где 
энергия
покоя частицы.
Формула (1) с учетом соотношений (2) и (3) запишется:
В нерелятивистском случае
,
(4)
в релятивистском случае
.
(5)
Сравним кинетические энергии
электрона, прошедшего заданные в условии задачи разности потенциалов 
и 
, с энергией
покоя электрона и в зависимости от этого решим, какую из формул (4) и (5) следует
применить для вычисления длины волны де Бройля.
Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U,
.
В первом случае 
,
что много меньше энергии покоя электрона 
.
Следовательно, в этом случае можно применить формулу (4). Для упрощения расчетов
заметим, что 
.
Подставив это выражение в формулу (4), перепишем ее в виде
.
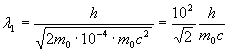Учитывая, что 
есть комптоновская длина волны 
,
получаем
.
Так как 
(см. табл. 1), то
.
Во втором случае кинетическая
энергия 
, т.е.
равна энергии покоя электрона. В этом случае необходимо применить релятивистскую
формулу (5). Учитывая, что 
,
по формуле (5) находим
,
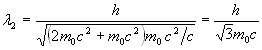или
.
Подставим значение
и произведем вычисления:
.
ПРИМЕР 3. Кинетическая энергия
электрона в атоме водорода составляет величину порядка 
.
Используя соотношение неопределенностей, оценить минимальные линейные размеры
атома.
РЕШЕНИЕ. Соотношение неопределенностей для координаты и импульса имеет вид
,
где 
неопределенность
координаты частицы (в данном случае электрона); 
неопределенность
импульса частицы (электрона); 
постоянная
Планка h, деленная на 
.
Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а, следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью
.
(1)
Соотношение неопределенностей (1) можно записать в этом случае в виде
,
откуда
.
(2)
Физически разумная неопределенность
импульса 
во
всяком случае не должна превышать значения самого р, т.е. 
.
Импульс р связан с кинетической энергией Т соотношением 
.
Заменим значением
(такая замена
не увеличит l). Переходя от неравенства к равенству, получим
.
Проверим, дает ли полученная формула единицу длины. Для этого в правую часть формулы (3) вместо символов величин подставим обозначения их единиц:
.
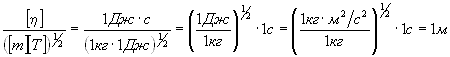Найденная единица является единицей длины.
Произведем вычисления:
.
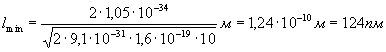ПРИМЕР 4. Волновая функция
описывает
основное состояние частицы в бесконечно прямоугольном ящике ширина l. Вычислить
вероятность нахождения частицы в малом интервале 
в
двух случаях: 1) вблизи стенки (
);
2) в средней части ящика 
.
РЕШЕНИЕ. Вероятность того, что частица будет обнаружена в интервале dx (от x до x+dx), пропорциональна этому интервалу и квадрату модуля волновой функции, описывающей данное состояние, равна
.
В первом случае искомая вероятность найдется интегрированием в пределах от 0 до 0,01l (рис. 37):
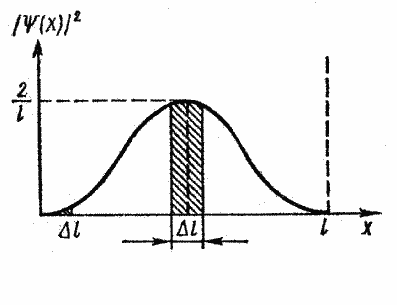
Рис.37
.
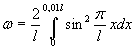(1)
Знак модуля опущен, так как
функция в данном
случае не является комплексной.
Так как x изменяется
в интервале 
и, следовательно, 
,
справедливо приближенное равенство
.
С учетом этого выражения (1) примет вид
.
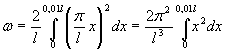После интегрирования получим
.
Во втором случае можно обойтись
без интегрирования, так как квадрат модуля волновой функции вблизи ее максимума
в заданном малом интервале 
практически не изменяется. Искомая вероятность во втором случае определяется
выражением
,
или
.
ПРИМЕР 5. Вычислить дефект
массы и энергии связи ядра 
.
РЕШЕНИЕ. Масса ядра всегда
меньше суммы масс свободных (находящихся вне ядра) протонов и нейтронов, из
которых ядро образовалось. Дефект массы ядра 
и есть разность между суммой масс свободных нуклонов (протонов и нейтронов)
и массой ядра, т.е.
,
(1)
где Z – атомный номер (число
протонов в ядре); А – массовое число (число нуклонов, составляющих ядро); 
соответственно
массы протона, нейтрона и ядра.
В справочных таблицах всегда
даются массы нейтральных атомов, но не ядер, поэтому формулу (1) целесообразно
преобразовать так, чтобы в нее входила масса 
нейтрального атома. Можно считать, что масса нейтрального атома равна сумме
масс ядра и электронов, составляющих электронную оболочку атома: 
,
откуда
.
(2)
Выразив в равенстве (1) массу
ядра по формуле (2), получаем 
,
или
.
Замечая, что 
,
масса атома
водорода, окончательно находим
.
(3)
Подставив в выражение (3) числовые значения масс (см. прил., табл. 15 и 17), получим
В соответствии с законом пропорциональности массы и энергии
,
(3)
где с – скорость света в вакууме.
Коэффициент пропорциональности
может быть выражен двояко:
или 
.
Если вычислить энергию связи,
пользуясь внесистемными единицами, то 
С учетом этого формула (3) примет вид
.
(4)
Подставив найденное значение дефекта массы ядра в формулу (4), получим
.
Примечание. Термин “дефект массы” часто
применяется в другом смысле: дефектом массы 
называют разность между массой нейтрального атома данного изотопа и его массовым
числом 
.Эта
величина особого физического смысла не имеет, но ее использование позволит в
ряде случаев значительно упростить вычисления. В настоящем пособии всюду имеется
в виду дефект массы 
,
определяемый формулой (1).
ПРИМЕР 6. При соударении
частицы с ядром
бора 
произошла
ядерная реакция, в результате которой образовалось два новых ядра. Одним из
этих ядер было ядро атома водорода 
.
Определить порядковый номер и массовое число второго ядра, дать символическую
запись ядерной реакции и определить ее энергетический эффект.
РЕШЕНИЕ. Обозначим неизвестное
ядра символом 
.
Так как 
частица
представляет собой ядро гелия 
,
запись реакции имеет вид
Применив закон сохранения числа
нуклонов, получим уравнение 
,
откуда А=13. Применив закон сохранения заряда, получим уравнение 
,
откуда Z=6. Следовательно, неизвестное ядро является ядром атома изотопа
углерода 
.
Теперь можем записать реакцию в окончательном виде:
Энергетический эффект Q ядерной реакции определяется по формуле
.
Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках – массы ядер – продуктов реакции. При числовых подсчетах по этой формуле массы ядер занимают массы нейтральных атомов. Возможность такой замены вытекает из следующий соображений.
Число электронов в электронной оболочке нейтрального атома равно его зарядовому числу Z. Сумма зарядовых чисел исходных ядер равна сумме зарядовых чисел ядер – продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода.
Очевидно, что при вычитании суммы масс нейтральных атомов углерода и водорода из суммы масс атомов гелия и бора массы электронов выпадут, и мы получим тот же результат, как если бы брали массы ядер. Подставив массы атомов (см. прил., табл. 15) в расчетную формулу, получим
.
ПРИМЕР 7. Определить начальную
активность 
радиоактивного препарата магния 
массой 
, а также
активность А через время t=6ч. Период полураспада 
магния считать известной.
РЕШЕНИЕ. Активность А изотопа характеризует скорость радиоактивного распада и определяется отношением числа dN ядер, распавшихся за интервал времени dt, к этому интервалу:
.
(1)
Знак “” показывает, что число N радиоактивных ядер с течением времени убывает.
Для того чтобы найти 
,
воспользуемся законом радиоактивного распада:
,
(2)
где N – число радиоактивных
ядер, содержащихся в изотопе, в момент времени t; 
число
радиоактивных ядер в момент времени, принятый за начальный (t=0);
λ – οостоянная радиационного распада.
Продифференцируем выражение (2) по времени:
.
(3)
Исключив из формул (1) и (3)
, находим
активность препарата в момент времени t:
.
(4)
Начальную активность 
препарата получим при t=0:
.
(5)
Постоянная радиоактивного распада
λ связана с периодом полураспада
соотношением
.
(6)
Число 
радиоактивных ядер, содержащихся в изотопе, равно произведению постоянной Авогадро
на количество
вещества v данного изотопа:
,
(7)
где m – масса изотопа, М – молярная масса.
С учетом выражений (6) и (7) формулы (5) и (4) принимают вид
,
(8) 
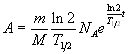. (9)
Произведем вычисления, учитывая,
что 
(см. прил.,
табл. 16); 
:
.
.
ПРИМЕР 8. Расстояние d между
соседними атомами кристалла кальция (решетка кубическая гранецентрированная)
равно 0,393нм. Определить: 1) параметр, а решетки; 2) плотность 
кристалла.
РЕШЕНИЕ. 1. Параметр, а решетки и расстояние d между ближайшими соседними атомами связаны простым геометрическим соотношением, ясным из рис. 38:
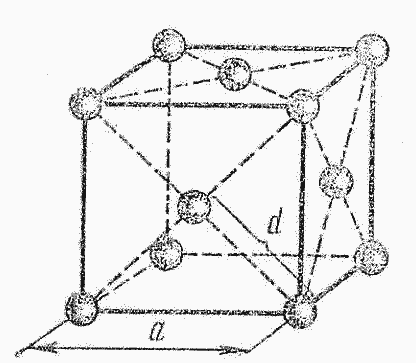
Рис.38
.
Произведем вычисления:
2. Плотность
кристалла связана с молярной массой М и молярным объемом 
соотношением
.
(1)
Молярный объем
найдем как произведение объема 
одной элементарной ячейки на число 
элементарных ячеек, содержащихся в одном моле кристалла:
.
(2)
Учитывая, что число элементарных
ячеек для кристалла, состоящего из одинаковых атомов, можно найти, разделив
постоянную Авогадро 
на число n атомов, приходящихся на одну элементарную ячейку, равенство
(2) можно записать в виде
.
(3)
Подставив в (1) выражение
из (2), получим
.
Произведем вычисления, учитывая, что число n в случае кубической гранецентрированной решетки равно 4:
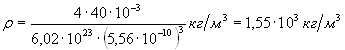
ПРИМЕР 9. Используя квантовую
теорию теплоемкости Эйнштейна, вычислить удельную теплоемкость с при постоянном
объеме алюминия при температуре Т=200К. Характеристическую температуру 
Эйнштейна принять для алюминия равной 300К.
РЕШЕНИЕ. Удельная теплоемкость
с вещества может быть выражена через молярную теплоемкость 
соотношением
,
(1)
где М – молярная масса.
Молярная теплоемкость при постоянном объеме по теории Эйнштейна выражается формулой
.
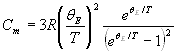(2)
Подставив в (1) выражение теплоемкости
по формуле
(2), получим
.
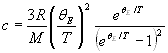(3)
Произведем вычисления:
.
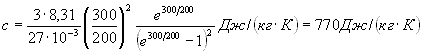ПРИМЕР 10. Определить теплоту
, необходимую
для нагревания кристалла NaCl массой m=20г от температуры 
до температуры 
.
Характеристическую температуру Дебая 
для NaCl принять равной 320К и условие 
считать выполненным.
РЕШЕНИЕ. Теплота ,
подводимая для нагревания тела от температуры 
и 
может быть
вычислена по формуле
,
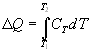(1)
где 
теплоемкость
тела.
Теплоемкость тела связана с молярной теплоемкостью соотношением
, (2)
Подставив выражение 
в формулу (1), получим
.
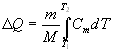(3)
В общем случае теплоемкость
есть сложная
функция температуры, поэтому выносить ее за знак интервала нельзя. Однако если
выполнено условие ,
то нахождение
облегчается тем, что можно воспользоваться предельным законом Дебая, в согласии
с которым теплоемкость пропорциональна кубу термодинамической температуры:
.
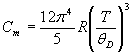(4)
Подставляя молярную теплоемкость (4) в формулу (3), получим
.
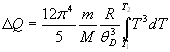Выполним интегрирование:
.
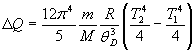Переписав полученную формулу
,
Произведем вычисления:
ПРИМЕР 11. Вычислить максимальную
энергию 
(энергию
Ферми), которую могут иметь свободные электроны в металле (медь) при температуре
Т=0К. Принять, что на каждый атом меди приходиться по одному электрону.
РЕШЕНИЕ. Максимальная энергия
, которую
могут иметь электроны в металле при Т=0К, связана с концентрацией n
свободных электронов соотношением
,
(1)
где 
постоянная
Планка; m – масса электрона.
Концентрация свободных электронов по условию задачи равна концентрации атомов, которая может быть найдена по формуле
,
(2)
где 
плотность
меди; 
постоянная
Авогадро; М – молярная масса.
Подставляя выражение n в формулу (1), получаем
.
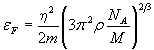Произведем вычисления:
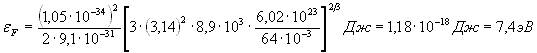
ПРИМЕР 12. Удельная проводимость
примесного полупроводника,
имеющего решетку типа алмаз, равна 110См/м. Считая, что полупроводник обладает
только дырочной проводимостью, определить: 1) концентрацию 
дырок; 2) подвижность 
дырок. Постоянную Холла 
принять равной 
.
РЕШЕНИЕ. 1. Концентрация
дырок связана с постоянной Холла, которая для полупроводников с решеткой типа
алмаз, обладающих носителями только одного знака, выражается формулой 
,
где е – элементарный заряд.
.
(1)
Произведем вычисления:
.
(2)
2. Удельная проводимость полупроводников выражается формулой
,
(3)
где 
и 
- концентрация
электронов и дырок; 
и 
- их подвижности.
При отсутствии электронной
проводимости первое слагаемое в скобках равно нулю и формула (3) принимает вид
, откуда
.
(4)
Подставим в (3) выражение
по формуле (1):
.
(5)
Произведем вычисления:
.
ПРИМЕР 13. Удельная магнитная
восприимчивость 
газообразной окиси азота (NO) при нормальных условиях 
.
Определить магнитный момент 
молекулы NO в магнетонах Бора.
РЕШЕНИЕ. Магнитная восприимчивость
парамагнитных веществ выражается по теории Ланжевена (при 
)
формулой
,
где 
магнитная
постоянная; n – концентрация молекул; 
магнитный
момент молекул; Т – термодинамическая температура; к – постоянная
Больцмана.
Из этой формулы
.
(1)
Входящая в выражение (1) магнитная
восприимчивость 
связана с заданной в условии задачи удельной магнитной восприимчивостью
соотношением
,
(2)
где 
плотность
вещества.
Плотность газа в соответствии с уравнением Менделеева-Клапейрона может быть выражена формулой
.
(3)
Перепишем выражение (1) с учетом соотношений (2) и (3):
.
Выразив в этом равенстве молярную
газовую постоянную R через постоянную Авогадро 
,
получим расчетную формулу для магнитного момента:
.
(4)
Произведем вычисления:
.
По условию задачи магнитный
момент следует выразить в магнетонах Бора. Так как 
(см. прил., табл. 1), то
