1 Понятие хэш-функции

Все рассмотренные ранее алгоритмы были связаны с задачей поиска, которую можно сформулировать следующим образом: задано множество ключей, необходимо так организовать это множество ключей, чтобы поиск элемента с заданным ключом потребовал как можно меньше затрат времени. Поскольку доступ к элементу осуществляется через его адрес в памяти, то задача сводится к определению подходящего отображения H множества ключей K во множество адресов элементов A.

Рисунок 27 - Отображение

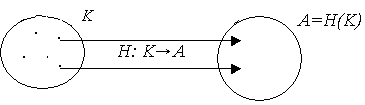
В предыдущих главах такое отображение получалось путем различного размещения ключей (в отсортированном порядке, в виде деревьев поиска), т.е. каждому ключу соответствовал свой адрес в памяти. Теперь рассмотрим задачу построения отображения H: K→A при условии, что количество всевозможных ключей существенно больше количества адресов. Будем обозначать это так: |K| >> |A|. Например, в качестве множества ключей можно взять всевозможные фамилии студентов до 15 букв (|K|= 32¹⁵), а в качестве множества адресов – 100 мест в аудитории (|A|=100). Функция H: K→A, определенная на конечном множестве K, называется хеш-функцией, если |K| >> |A|. Таким образом, хеш-функция допускает, что нескольким ключам может соответствовать один адрес. Хеширование – один из способов поиска элементов по ключу, при этом над ключом k производят некоторые арифметические действия и получают значение функции h=H(k), которое указывает адрес, где хранится ключ k и связанная с ним информация. Если найдутся ключи k_i ≠ k_j, для которых H(k_i)=H(k_j), т.е. несколько ключей отображаются в один адрес, то такая ситуация называется коллизией (конфликтом).

Если данные организованы как обычный массив, то H – отображение ключей в индексы массива. Процесс поиска происходит следующим образом:

1. для ключа k вычисляем индекс h=H(k)
2. проверяем, действительно ли h определяет в массиве T элемент с ключом k, т. е. верно ли соотношение T[H(k)].data = k. Если равенство верно, то элемент найден. Если неверно, то возникла коллизия.

Для эффективной реализации поиска с помощью хеш-функций необходимо определить какого вида функцию H нужно использовать и что делать в случае коллизии (конфликта). Хорошая хеш-функция должна удовлетворять двум условиям:

1. её вычисление должно быть очень быстрым
2. она должна минимизировать число коллизий, т.е. как можно равномернее распределять ключи по всему диапазону индекса.

Для разрешения коллизий нужно использовать какой-нибудь способ, указывающий альтернативное местоположение искомого элемента. Выбор хеш-функции и выбор метода разрешения коллизий – два независимых решения.

Функции, дающие неповторяющиеся значения, достаточно редки даже в случае довольно большой таблицы. Например, знаменитый парадокс дней рождений утверждает, что если в комнате присутствует не менее 23 человек, имеется хороший шанс, что у двух из них совпадет день рождения. Т.е., если мы выбираем функцию, отображающую 23 ключа в таблицу из 365 элементов, то с вероятностью 0,4927 все ключи попадут в разные места.

Теоретически невозможно так определить хеш-функцию, чтобы она создавала случайные данные из неслучайных реальных ключей. Но на практике нетрудно сделать достаточно хорошую имитацию случайности, используя простые арифметические действия.

Будем предполагать, что хеш-функция имеет не более m различных значений: 0≤H(k)<m для любого значения ключа. Например, если ключи десятичные, то возможен следующий способ. Пусть m=1000, в качестве H(k) можно взять три цифры из середины двадцатизначного произведения k•k. Этот метод “середины квадрата”, казалось бы, должен давать довольно равномерное распределение между 000 и 999. но на практике такой метод не плох, если ключи не содержат много левых или правых нулей подряд.

Исследования выявили хорошую работу двух типов хеш-функций: один основан на умножении, другой на делении.

1. метод деления особенно прост: используется остаток от деления на m H(K)=K mod m. При этом желательно m брать простым числом.
2. метод умножения H(K)=2^m(A∙K mod w), где A и w взаимно простые числа.

Далее будем использовать функцию H(k)=ORD(k) mod m, где ORD(k) – порядковый номер ключа, m – размер массива (таблицы), причем m рекомендуется брать простым числом.

Если ключ поиска является строкой, то для вычисления ее хеш-номера будем рассматривать её как большое целое число, записанное в 256-ичной системе счисления (каждый символ строки является цифрой), т.е.

H(S₁S₂S₃…S_t)=(S₁∙256^t-1+S₂∙256^t-2+…+S_t-1 256+S_t) mod m .

Используя свойства остатка от деления можно легко вычислить подобные выражения: (a+b)∙mod m=(a mod m + b mod m) mod m. Например, (47+56) mod 10 = (7+6) mod 10 = 3

Алгоритм на псевдокоде

Вычисление хеш-функции для строки S

Обозначим t – длина строки S

h:=0

DO (i=1,2,…,t)

   h:=(h∙256+S_i) mod m

OD

2 Метод прямого связывания

Рассмотрим метод устранения коллизий путем связывания в список всех элементов с одинаковыми значениями хеш-функции, при этом необходимо m списков. Включение элемента в хэш-таблицу осуществляется в два действия:

1) вычисление i=H(k)

2) добавление элемента k в конец i-того списка

Поиск элемента также требует два действия:

1) вычисление i=H(k)

2) последовательный просмотр i-того списка.

Пример. Составить хеш-таблицу для строки КУРАПОВА ЕЛЕНА. Будем использовать номера символов в алфавитном порядке. Пусть m=5,

H(k)=ORD (k mod 5)

Вычислим значения хэш-функции для символов строки

H(К)=11 mod 5=1

H(У)=20 mod 5=0

H(Р)=17 mod 5=2

H(А)=1 mod 5=1

H(П)=16 mod 5=1

H(О)=15 mod 5=0

H(В)=3 mod 5=3

H(Е)=6 mod 5=1

H(Л)=12 mod 5=2

H(Н)=14 mod 5=4

Объединим символы с одинаковыми хеш-номерами в один список

Рисунок 28 - Хеш-таблица, построенная методом прямого связывания

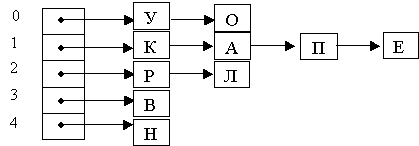
Оценим трудоемкость поиска в хеш-таблице, построенной методом прямого связывания. Пусть n – количество элементов данных, m – размер хеш-таблицы. Если все ключи равновероятны и равномерно распределены по хеш-таблице, то средняя длина списка будет . При поиске в среднем нужно просмотреть половину списка. Поэтому C_ср=. Если n<m, то С_ср<2, т. е. в большинстве случаев достаточно одного сравнения. Объем дополнительной памяти определяется объемом памяти, необходимой для хранения (m+n) указателей. Известно, что трудоемкость поиска с помощью двоичного дерева: С_ср=log n, объем дополнительной памяти – 2n указателей. Метод прямого связывания становится более эффективным, чем дерево поиска, когда

,

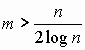
Если n=1000, то при m>50 (m=53) метод прямого связывания более эффективен, чем дерево поиска, причем экономия памяти составит около 4 Кбайт. Можно сэкономить еще больше памяти, если отказаться от списков и размещать данные в самой хеш-таблице.

3 Метод открытой адресации

Рассмотрим метод открытой адресации, который применяется для разрешения коллизий при поиске с использованием хеш-функций. Суть метода заключается в последовательном просмотре различных элементов таблицы, пока не будет найден искомый ключ k или свободная позиция. Очевидно, необходимо иметь правило, по которому каждый ключ k определяет последовательность проб, т.е. последовательность позиций в таблице, которые нужно просматривать при вставке или поиске ключа k. Если мы произвели пробы и обнаружили свободную позицию, то ключа k нет в таблице. Таким образом, коллизия устраняется путем вычисления последовательности вторичных хеш-функций:

h₀=h(x)

h₁=h(x)+g(1) (mod m)

h₂=h(x)+g(2) (mod m)

h_i=h(x)+g(i) (mod m)

Самое простое правило для просмотра – просматривать подряд все следующие элементы таблицы. Этот прием называется методом линейных проб, при этом g(i)=i, i=1,2,…,m-1. Недостаток данного метода – плохое рассеивание ключей (ключи группируются вокруг первичных ключей, которые были вычислены без конфликта), хотя и используется вся хеш-таблица.

Если в качестве вспомогательных функций использовать квадратичные, т.е. g(i)=i², i=1,2,…,m-1, то такой способ просмотра элементов называется методом квадратичных проб. Достоинство этого метода – хорошее рассеивание ключей, хотя хеш-таблица используется не полностью.

Утверждение. Если m – простое число, то при квадратичных пробах просматривается по крайней мере половина хеш-таблицы.

Доказательство. Пусть i-ая и j-ая пробы, i<j, приводят к одному значению h, т.е. h_i=h_j. Тогда i² mod m=j² mod m

(j² – i²) mod m=0

(j+i)(j-i) mod m=0

(j+i)(j-i)=km

i+j=km/(j-i)

Если m – простое число, то k/(j-i) – целое число больше нуля. В худшем случае k/(j-i)=1, тогда i+j=m и j>m/2. (Если m – не простое число, то k/(j-i) не обязательно должно быть целым).

На практике этот недостаток не столь существенен, т.к. m/2 вторичных попыток при разрешении конфликтов встречаются очень редко, главным образом в тех случаях, когда таблица почти заполнена.

Итак, нам нужно вычислять

h₀=h(x)

h_i=(h₀+i²) mod m, i>0

Вычисление h_i требует одного умножения и деления. Покажем, как можно избавиться от этих операций. Произведем несколько первых шагов при вычислении h_i.

h₁=h₀+1

h₂=h₀+4=h₀+1+3=h₁+3 (mod m)

h₃=h₀+9=h₀+4+5=h₂+5 (mod m)

…

Нетрудно видеть, что возникает рекуррентное соотношение:

d_0<=1, h₀=h(x)

h_i+1=h_i+d_i (mod m)

d_i+1=d_i+2

Поскольку h_i<m, d_i<m, то можно избавиться от деления, заменив его вычитанием h=h-m (см. алгоритм).

Алгоритм на псевдокоде

Поиск и вставка элемента с ключом x

Пусть хеш-таблица является массивом A=(a₀, a₁, … , a_m-1), сначала заполненный нулями. Пусть x≠0.

h:=x mod m

d:=1

DO

   IF (a_h=x) элемент найден OD

   IF (a_h=0) ячейка пуста, a_h:=x OD

   IF (d≥m) переполнение таблицы OD

   h:=h+d

   IF (h≥m) h:=h-m FI

   d:=d+2

OD

Заметим, что если нужен только поиск, то необходимо исключить операцию a_h:=x.

Пример построения хеш-таблицы методом квадратичных проб (m=11) для строки ВЛАДИМИР ПУТИН. Номера символов данной строки приведены в таблице.

Таблица 3 - Номера символов строки

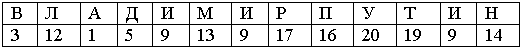
Для каждого символа вычисляем его хеш-номер (или последовательность хеш-номеров, если потребуется) и в соответствии с вычисленным номером заносим символ в хеш-таблицу.

В: h₀=3 mod 11=3

Л: h₀=12 mod 11=1

А: h₀=1 mod 11=1

     h₁=1+1=2

Д: h₀=5

И: h₀=9

М: h₀=13 mod 11=2

     h₁=2+1=3

     h₂=3+3=6

Р: h₀=17 mod 11=6

     h₁=6+1=7

П: h₀=16 mod 11=5

     h₁=5+1=6

     h₂=6+3=9

     h₃=9+5=3

     h₄=3+7=10

У: h₀=20 mod 11=9

     h₁=9+1=10

     h₂=10+3=13 mod 11=2

     h₃=2+5=7

     h₄=7+7=14 mod 11=3

     h₅=3+9=12 mod 11=1

Просмотр элементов хеш-таблицы на этом заканчивается несмотря на то, что в таблице еще имеются незаполненные ячейки, поскольку следующее значение d уже не будет строго меньше m=11. Таким образом, для данной строки не удается построить хеш-таблицу с m=11. Заполненная часть хеш-таблицы выглядит следующим образом

Рисунок 29 - Использование квадратичных проб

Контрольные вопросы

1. Что такое хэш-функция?
2. Что такое коллизия?
3. Как осуществляется поиск с помощью хэш-таблицы?
4. Какие способы построения хэш-таблиц Вы знаете?