где магнитная проницаемость изотропной среды; магнитная постоянная. В вакууме и тогда магнитная индукция в вакууме

или

где магнитная индукция поля, создаваемого элементом проводника длиной с током : r – радиус-вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; угол между радиус-вектором и направлением тока в элементе проводника.

где R – радиус кругового витка.

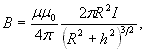
где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

где расстояние от оси проводника до точки, в которой определяется магнитная индукция.

 Рис.25

Обозначения ясны из рисунка. Направление вектора магнитной индукции В обозначено точкой – это значит, что В направлен перпендикулярно плоскости чертежа к нам.

При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (рис. 25,б) тогда

где n – отношение числа витков соленоида к его длине.

или

где l – длина проводника; угол между направлением тока в проводнике и вектором магнитной индукции В. Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применить к каждому элементу проводника в отдельности:

где d – расстояние между проводами.

где n – единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.

или

где угол между векторами и В.

или

где Q – заряд частицы; m – масса частицы.

или

где v – скорость заряженной частицы; угол между векторами v и В.

а) в случае однородного магнитного поля и плоской поверхности

или

где S – площадь контура; угол между нормалью к плоскости контура и вектором магнитной индукции:

б) в случае неоднородного поля и произвольной поверхности

(интегрирование ведется по всей поверхности).

Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

где l – длина проводника; угол между векторами v и B.

или

где R – сопротивление контура.

где n – отношение числа витков соленоида к его длине; V – объем соленоида.

а) (при замыкании цепи),

где э. д. с. источника тока; t – время, прошедшее с момента размыкания цепи;

б) (при размыкании цепи),

где сила тока в цепи при t = 0; t – время, прошедшее с момента размыкания цепи.

или или

где В – магнитная индукция; Н – напряженность магнитного поля.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПРИМЕР 1. По длинному прямому тонкому проводу течет ток силой Определить магнитную индукцию В поля, создаваемого проводником в точке, удаленной от него на расстояние

РЕШЕНИЕ. Магнитное поле, создаваемое прямым бесконечно длинным проводником ничтожно малого сечения, обладает осевой симметрией. Это значит, что модуль вектора магнитной индукции в данной точке будет зависеть только от ее расстояния до проводника. Поэтому все точки на окружности радиусом r (рис. 26), лежащей в плоскости, перпендикулярной проводнику, будут характеризоваться одинаковой по модулю магнитной индукцией

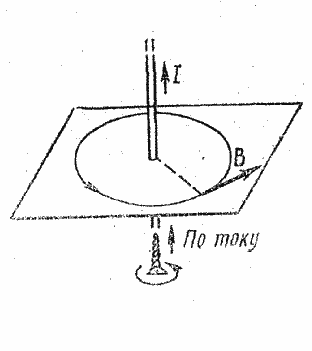
 Рис.26

(1)

где магнитная постоянная.

Направление вектора В зависит от положения точки на окружности и направление тока в проводнике. Этот вектор направлен по касательной к проведенной нами окружности (это следует из закона Био-Савара-Лапласа, записанного в векторной форме.) Окружность на рис. 26 является магнитной силовой линией. Ее направление (а значит, и направление вектора В) определяется по правилу правого винта:

Произведем вычисления:

ПРИМЕР 2. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении электрические токи силой расположены на расстоянии друг от друга. Определить магнитную индукцию В поля, создаваемого проводниками с током в точке А (рис. 27), отстоящей от оси одного проводника на расстоянии от другого -

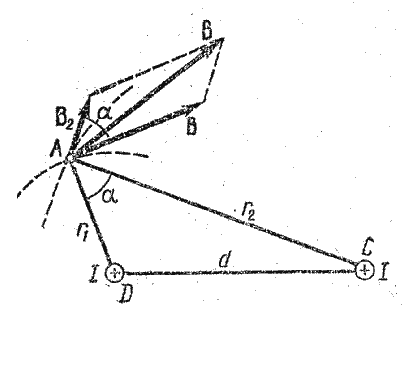
 Рис.27

РЕШЕНИЕ. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукций и полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:

Модуль вектора В может быть найден по теореме косинусов:

(1)

где угол между векторами и

Магнитная индукция и выражаются соответственно через силу тока I и расстояние и от проводов до точки А:

Подставляя выражения и в формулу (1) и вынося за знак корня, получаем

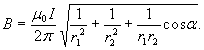(2)

Вычислим Заметив, что (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем

где расстояние между проводами. Отсюда

Подставим в формулу (2) числовые значения физических величин и произведем вычисления:

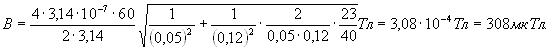
ПРИМЕР 3. По проводу, согнутому в виде квадрата со стороной течет ток силой Найти магнитную индукцию В в точке О пересечения диагоналей квадрата.

РЕШЕНИЕ. Расположим квадратный виток в плоскости чертежа (рис.28).

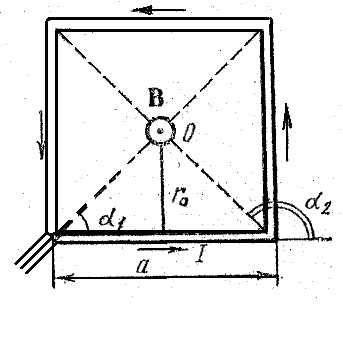
 Рис.28

Согласно принципу суперпозиций магнитных полей

(1)

где магнитные индукции полей, создаваемых токами, протекающими по каждой стороне квадрата.

В точке О пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости витка “к нам”. Кроме того, из соображений симметрии следует, что модули этих векторов одинаковы: Это позволяет векторное равенство (1) заменить скалярным:

(2)

Магнитная индукция поля, создаваемого отрезком прямолинейного провода с током, выражается формулой

(3)

Учитывая, что и (рис. 28), формулу (3) можно переписать в виде

Подставив выражение в формулу (2), найдем

Заметив, что и (так как ), получим

Проверим, дает ли расчетная формула единицу магнитной индукции. Для этого в правую часть формулу вместо символов величин подставим обозначения их единиц:

Найденная единица является единицей магнитной индукции.

Произведем вычисления:

ПРИМЕР 4. Плоский квадратный контур со стороной по которому течет ток силой свободно установился в однородном магнитном поле (). Определить работу А, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1) 2)При повороте контура сила тока в нем поддерживается неизменной.

РЕШЕНИЕ. Как известно, на контур с током в магнитном поле действует момент силы (рис. 29):

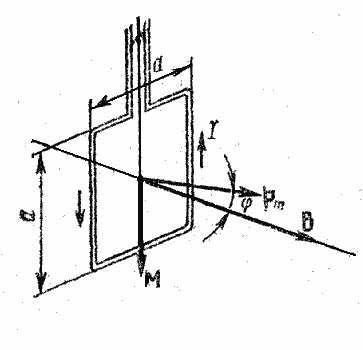
 Рис.29

(1)

где магнитный момент контура; В – магнитная индукция; угол между векторами (направлен по нормали к контуру) и В. По условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (М=0), а значит, , т.е векторы и В сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил [см. (1)] будет стремиться возвращать контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота ), то для подсчета работы применим формулу работы в дифференциальной форме . Учитывая формулу (1), получаем

.

Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:

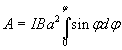. (2)

Работа при повороте на угол :

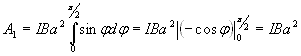. (3)

Выразим числовые значения величин в единицах СИ: и подставим в (3):

.

Работа при повороте на угол . В этом случае, учитывая, что угол мал, заменим в выражении (2) :

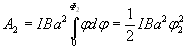. (4)

Выразим угол в радианах. После подстановки числовых значений в (4) найдем

.

Задачу можно решить и другим способом. Работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур:

где магнитный поток, пронизывающий контур до перемещения: то же, после перемещения.

Если , то . Следовательно, что совпадает с (3).

ПРИМЕР 5. Электрон, пройдя ускоряющую разность потенциалов , попал в однородное магнитное поле напряженностью . Определить радиус R кривизны траектории и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.

РЕШЕНИЕ. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости, следовательно, сообщает электрону нормальное ускорение. По второму закону Ньютона , где норма, или

, (1)

где е – элементарный заряд; скорость электрона; В – магнитная индукция; m – масса электрона; R – радиус кривизны траектории; угол между вектором v и B (в данном случае и ).

Из формулы (1) найдем

. (2)

Входящий в равенство (2) импульс может быть выражен через кинетическую энергию Т электрона:

. (3)

Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством

.

Подставив выражение Т в формулу (3), получим

.

Магнитная индукция В может быть выражена через напряженность Н поля в вакууме:

,

где магнитная постоянная.

Подставив выражения В и в формулу (2), определим

. (4)

Произведем вычисления:

.

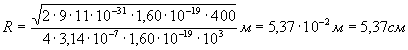Для определения частоты обращения воспользуемся формулой, связывающей частоту со скоростью и радиусом:

. (5)

Подставив в формулу (5) выражение (2), получим

, или .

Произведем вычисления:

.

ПРИМЕР 6. В однородном магнитном поле () равномерно с частотой вращается рамка, содержащая , плотно прилегающие друг к другу. Площадь S рамки равна 150 . Определить мгновенное значение э. д. с. индукции , соответствующего угла поворота рамки, равному .

РЕШЕНИЕ. Мгновенное значение э. д. с. индукции определяется основным уравнением электромагнитной индукции Фарадея-Максвелла:

, (1)

где потокосцепление.

Потокосцепление связано с магнитным потоком Ф и числом N витков, плотно прилегающих друг к другу, соотношением

. (2)

Подставляя выражения в формулу (1), получаем

. (3)

При вращении рамки (рис. 30) магнитный поток Ф, пронизывающий рамку в момент времени t, определяется соотношением:

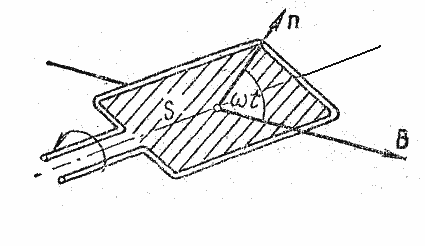
 Рис.30

,

где В – магнитная индукция; S – площадь рамки; круговая (или циклическая) частота.

Подставив в формулу (2) выражение Ф и продифференцировав полученное выражение по времени, найдем мгновенное значение э. д. с. индукции:

. (4)

Круговая частота связана с частотой вращения n соотношением

.

Подставляя выражение в формулу (3) и заменив на , получим

.

Произведем вычисления:

.

ПРИМЕР 7. Соленоид с сердечником из немагнитного материала содержит витков провода, плотно прилегающих друг к другу. При силе тока магнитный поток . Определить индуктивность L соленоида и энергию W магнитного поля соленоида.

РЕШЕНИЕ. Индуктивность L связана с потокосцеплением и силой тока I соотношением.

. (1)

Потокосцепление, в свою очередь, может быть определено через поток Ф и число витков N (при условии, что витки плотно прилегают друг к другу):

. (2)

Из формул (1) и (2) находим индуктивность соленоида:

. (3)

Энергия магнитного поля соленоида:

.

Выразив L согласно (3), получим

  (4)

Подставим в формулу (3) и (4) значения физических величин и произведем вычисления:

.